概率密度函数,这种方法能够表示随机变量每个取值有多大的可能性。
概率密度函数
正态分布的概率密度函数均值为μ 方差为σ2 (或标准差σ)是高斯函数的一个实例:
-
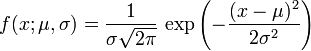 。
。
(请看指数函数以及π.)
如果一个随机变量X服从这个分布,我们写作 X ~ N(μ,σ2). 如果μ = 0并且σ = 1,这个分布被称为标准正态分布,这个分布能够简化为
-
 。
。
右边是给出了不同参数的正态分布的函数图。
正态分布中一些值得注意的量:
- 密度函数关于平均值对称
- 平均值是它的众数(statistical mode)以及中位数(median)
- 函数曲线下68.268949%的面积在平均值左右的一个标准差范围内
- 95.449974%的面积在平均值左右两个标准差2σ的范围内
- 99.730020%的面积在平均值左右三个标准差3σ的范围内
- 99.993666%的面积在平均值左右四个标准差4σ的范围内
- 反曲点(inflection point)在离平均值的距离为标准差之处
累积分布函数
累积分布函数是指随机变量X小于或等于x的概率,用密度函数表示为
正态分布的累积分布函数能够由一个叫做误差函数的特殊函数表示:
标准正态分布的累积分布函数习惯上记为Φ,它仅仅是指μ = 0,σ = 1时的值,
将一般正态分布用误差函数表示的公式简化,可得:
它的反函数被称为反误差函数,为:
该分位数函数有时也被称为probit函数。probit函数已被证明没有初等原函数。
正态分布的分布函数Φ(x)没有解析表达式,它的值可以通过数值积分、泰勒级数或者渐进序列近似得到。
性质
正态分布的一些性质:
- 如果
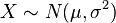 且a与b是实数,那么aX + b∼N(aμ + b,(aσ)2) (参见期望值和方差).
且a与b是实数,那么aX + b∼N(aμ + b,(aσ)2) (参见期望值和方差). - 如果
 与
与 是统计独立的正态随机变量,那么:
是统计独立的正态随机变量,那么:
- 它们的和也满足正态分布
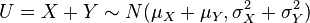 (proof).
(proof). - 它们的差也满足正态分布
 .
. - U与V两者是相互独立的。
- 它们的和也满足正态分布
- 如果
 和
和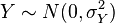 是独立正态随机变量,那么:
是独立正态随机变量,那么:
- 它们的积XY服从概率密度函数为p的分布
-
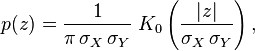 其中K0是贝塞尔函数(modified Bessel function)
其中K0是贝塞尔函数(modified Bessel function)
-
- 它们的比符合柯西分布,满足X / Y∼Cauchy(0,σX / σY).
- 它们的积XY服从概率密度函数为p的分布
- 如果
 为独立标准正态随机变量,那么
为独立标准正态随机变量,那么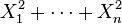 服从自由度为n的卡方分布。
服从自由度为n的卡方分布。








 本文介绍了正态分布的概率密度函数及累积分布函数的基本概念,并详细阐述了正态分布的特性,包括其对称性、常见统计量的分布区间以及与其他随机变量的关系。
本文介绍了正态分布的概率密度函数及累积分布函数的基本概念,并详细阐述了正态分布的特性,包括其对称性、常见统计量的分布区间以及与其他随机变量的关系。



![\Phi(z)=\frac12 \left[1 + \mathrm{erf}\,(\frac{z-\mu}{\sigma\sqrt2})\right] .](http://upload.wikimedia.org/wikipedia/zh/math/3/0/9/309df22a79a5687e1891cfbcbae2db89.png)

![\Phi(z)=\frac{1}{2} \left[ 1 + \operatorname{erf} \left( \frac{z}{\sqrt{2}} \right) \right].](http://upload.wikimedia.org/wikipedia/zh/math/d/0/5/d052159a00aa278a29d101a5c2b59353.png)
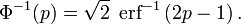
















 6131
6131

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








