统计学习方法--学习笔记----6.1.1 Logistic 回归 （拟牛顿法- DFP算法）

6.1.1 Logistic 回归 （拟牛顿法- DFP算法）

Logistic 回归模型类似，具体信息参考 （梯度下降法）

对数似然函数为：

L(w) = ∑[yi*log( π(xi) )+(1-yi)*log(1- π(xi) )]

=∑[yi* (w ∙ xi) - log(1+exp (w ∙ xi) ]

问题转变：

问题由模型参数选择，变为选取合适的w使得L(w)最大化，即目标函数最优化的问题

----------------------------------------------------------------------------------------------------------------

• 运用牛顿法 / 拟牛顿法：

牛顿法简述：

f(x) 在 xk附近进行二阶泰勒展开：

f(x) = f(xk)+[∇f(xk)] T ∙ (x-xk)+1/2*(x-xk) T ∙ (H(xk)) ∙ (x-xk)

= f(xk)+[g(xk)] T ∙ (x-xk)+1/2*(x-xk) T ∙ (H(xk)) ∙ (x-xk) -----------------------(B.2)

其中，g(xk) = ∇f(xk)为f(x)的梯度向量在xk的值，

H(xk)为f(x)的海赛矩阵 Hesse Matrix:

边界条件：在极值点 ∇f(x)=0

将x_k+1带入：

∇f(x) = gk + Hk(x-xk) = gk + Hk(x k+1 -x k )=0 ................... (B.6)

-->

迭代公式：

x k+1 = x k - Hk^ -1 ∙ gk

即：

x k+1 = x k + pk

其中： Hk ∙ pk = - gk

迭代的过程中，因为需要求Hk的逆矩阵，故运算量比较大，为了规避这部分运算量，采用拟牛顿法

拟牛顿法( DFP算法) 简述：

拟牛顿法的核心是：Gk 近似于 Hk^-1 ，对Gk迭代，从而求解 x

由公式B.6:

∇f(x) = gk + Hk(x-xk) = gk + Hk(x k+1 -x k )

当 x = x k+1 , g k+1 -gk = Hk(x k+1 -x k )

令yk = g k+1 -gk, δk = x k+1 -x k ，

则：yk = Hk ∙ δk

拟牛顿条件：G k+1 ∙ yk = δk (G k+1 )

(？？至于此处为什么是G k+1，而非Gk，尚不理解？？)

DFP算法：

Gk+1 = Gk + [δk ∙( δk) T ] / [ ( δk) T ∙yk ] - [Gk ∙yk∙( δk) T ∙ Gk] / [ ( yk) T ∙ Gk ∙yk ]

算法实现：

初值：

初始点 x0, 算出 ∇f(x0) = g0, H(x0) -->G0=H0^-1

p0 = -G0 ∙ g0

迭代：

pk: pk = -Gk ∙ gk

λk:

一维搜索 λk，使得 f(xk + λk*pk) = min f(xk + λ*pk)

[解释：引入 λk 是为了加快迭代的步骤，尽快到达最小值

令 x = xk - λ 0 * Hk^-1 * gk ，将 x 带入二阶泰勒展开 (B.2)：

得到：

f(x) = f(xk) - (λ 0 - λ 0 ^2/2) * [g(xk)] T ∙ Hk^-1 ∙ gk

当λ 0 - λ 0 ^2/2为正数，f(x k+1 ) 为单调下降

令λk = λ 0 - λ 0 ^2/2，则 λk 的取值范围为 0<λk<2

]

运算中λk取值方法：初值为0，间隔0.1，增加至1.9，λk = 0, 0.1, 0.2, ....1.9

x k+1 : x k+1 = xk + λk * pk

g k+1 : g k+1 = g(x k+1 )

G k+1 : G k+1 = Gk + [δk ∙( δk) T ] / [ ( δk) T ∙yk ] - [Gk ∙yk∙( δk) T ∙ Gk] / [ ( yk) T ∙ Gk ∙yk ]

迭代停止条件：

|| g k+1 || < ε (本例中取 ε = 10^-8)

----------------------------------------------------------------------------------------------------------------

• 具体到Logistic 回归：

最初运算公式

已知条件：X，Y，待求 w

X * w = z 目标值：Y

由 L(w) =∑[yi* (w ∙ xi) - log(1+exp (w ∙ xi) ]

一阶导数：

#∂L/∂wi=∑ [xki*yk + xki/(1+exp(-x[k]*w) - xki], (k=1,2,..,m)

二阶导数：

#∂2L/∂wi∂wj = ∑[(-1)*x_ki*x_kj*exp(x[k]*w)*(1+exp(x[k]*w))^-2], (k=1,2,..,m)

• 代码：

import numpy as np

from math import *

from numpy import *

#L(w)=∑[yi*(xi*w)-log(1+exp(xi*w))]，求该函数的最小值

def quasi_Newton_DFP(dataMatIn, classLabels, numIter):

dataMatrix = mat(dataMatIn) #X: convert to numpy.matrixlib.defmatrix.matrix

labelMat = mat(classLabels).transpose() #Y: convert to NumPy matrix，再转置

m,n = shape(dataMatrix)

wk = mat(ones((n,1))) #wk初始化为[1,1,1]

# 计算初始二阶导数（海赛矩阵） #∂2L/∂wi∂wj = ∑[(-1)*x_ki*x_kj*exp(x[k]*w)*(1+exp(x[k]*w))^-2]

H0 = mat(eye(n,M=None,k=0))

for i in range(n):

for j in range(n):

H0[i,j]=0

for k in range(m):

H0[i,j]=H0[i,j]+(dataMatrix[k,i]*dataMatrix[k,j]*exp(dataMatrix[k]*wk))/(1+exp(dataMatrix[k]*wk))

Gk = numpy.linalg.inv(H0) #Gk：用H0的逆矩阵初始化G0，G0 ~ H0^-1

'''

a, b = numpy.linalg.eig(H0) #特征值与特征向量，a为特征值 向量，b为特征向量矩阵

c=np.empty((n), dtype=float)

for i in range(n):

c[i] = 1/a[i]

Gk =numpy.diag(c) #Gk：用H0的特征值的导数作为特征值初始化G0，G0 ~ H0^-1

'''

#一阶导数初值 g0 #∂L/∂wi=∑ [xki*yk + xki/(1+exp(-x[k]*w) - xki]

gk = mat(zeros((n,1)))

for i in range(n): #计算gk+1

for k in range(m):

gk[i] = gk[i] + dataMatrix[k,i]*labelMat[k]+ dataMatrix[k,i]/(1+exp(dataMatrix[k]*wk) - dataMatrix[k,i])

norm_gk = math.sqrt(float(gk.transpose()*gk)) #向量gk的范数

La =0 #λ(Lambda), f(xk+λ*pk)

L =0 #L(w)=∑[yi*(xi*w)-log(1+exp(xi*w))]

for iv in range(numIter): #最多迭代numIter次

if norm_gk < 10^-8:

break

pk = -Gk*gk

La_min = 0

Lmin = 0 #min f(xk + λ*pk): Lmin

L = 0

for l in range(20):

La = float(l/10.0) #λ(Lambda), 在0~1.9之间找一个值，使 f(xk + λ*pk)最小

wk_temp = wk + La*pk

for ii in range(m):

L = L + labelMat[ii]*(dataMatrix[ii]*wk_temp) - math.log(1+math.exp(dataMatrix[ii]*wk_temp)) #F: f(xk+λ*pk), 即 L(w)=∑[yi*(xi*w)-log(1+exp(xi*w))]

if L<Lmin:

Lmin = L

La_min = La

wk = wk + La_min*pk

dk = La_min*pk #δk Delta k

z = dataMatrix * wk

gk_old = gk

for i in range(n): #计算gk+1

x_mi= mat([x[i] for x in dataMatIn])

SH = 0

for j in range(m):

SH = SH + (-1)*(exp(z[j]*dataMatrix[j,i]))/(1+exp(z[j])) #Second half: - 1/(1+exp(-(x*w)))

gk[i] = x_mi*labelMat + SH

norm_gk = math.sqrt(float(gk.transpose()*gk))

yk = gk - gk_old # yk = gk+1 - gk

Gk = Gk+(dk*dk.transpose())/(dk.transpose()*yk)-(Gk*yk*yk.transpose()*Gk)/(yk.transpose()*Gk*yk)

return wk

• 运算结果比较（拟牛顿法 与 梯度下降法）：

数据源为 《机器学习实战》第5章，testSet.txt

拟牛顿法：

梯度下降

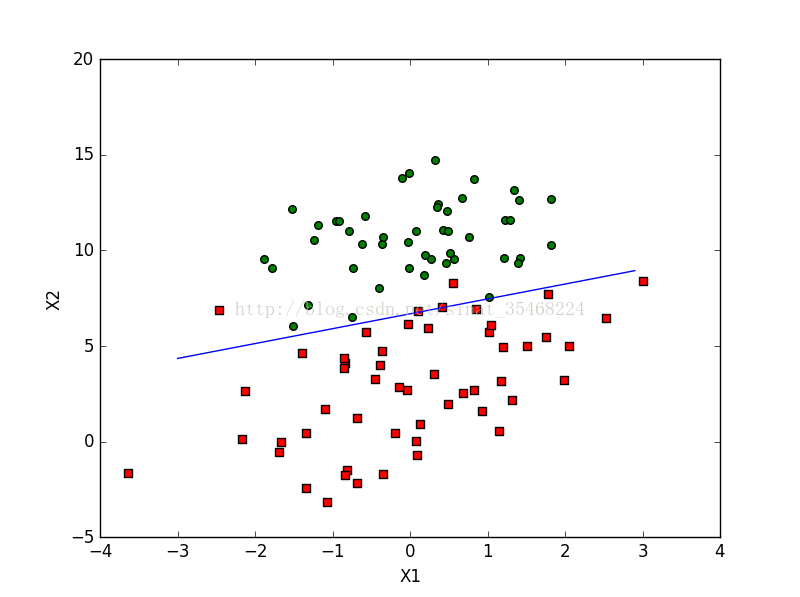
结论：

1. 速度：梯度下降法明显快很多，具体时间未测，大体差一个数量级

2. 本例模型拟合结果：未使用任何工具，单从直观感受，梯度下降误差更少

Reference：

文中模型和数据参考《机器学习》、《机器学习实战》、《统计学习方法》