分治——最近点对问题

利用分治方法的经典问题——最近点对问题（Closest pair of points problem）

问题描述

n个点在公共空间中，求出所有点对的欧几里得距离最小的点对。

问题分析

• 该题直观的解决方法便是Brute Force(暴力求解)。时间复杂度为$O（n^2）$。

minDist = infinity
for i = 1 to length(P) - 1
 for j = i + 1 to length(P)
  let p = P[i], q = P[j]
  if dist(p, q) < minDist:
   minDist = dist(p, q)
   closestPair = (p, q)
return closestPair

• 利用分治思想进行求解。首先分析题目，符合分治法的适用条件，规模越小容易求解，同时具有最优子结构。

分治法求解

• 分解
  • 对所有的点按照x坐标（或者y）从小到大排序（排序方法时间复杂度$O(nlogn)$）。
  • 根据下标进行分割，使得点集分为两个集合。
• 解决
  • 递归的寻找两个集合中的最近点对。
  • 取两个集合最近点对中的最小值$min(di{s}_{left}，di{s}_{right})$。
• 合并
  • 最近距离不一定存在于两个集合中，可能一个点在集合A，一个点在集合B，而这两点间距离小于dis。

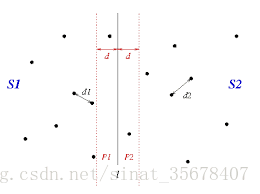
这其中如何合并是关键。根据递归的方法可以计算出划分的两个子集中所有点对的最小距离$di{s}_{left}，di{s}_{right}$，再比较两者取最小值，即$dis=min(di{s}_{left}，di{s}_{right})$。那么一个点在集合A，一个在集合B中的情况，可以针对此情况，用之前分解的标准值，即按照x坐标（或者y）从小到大排序后的中间点的x坐标作为mid，划分一个$[mid-dis,mid+dis]$区域，如果存在最小距离点对，必定存在这个区域中。

之后只需要根据$[mid-dis,mid]$左边区域的点来遍历右边区域$[mid,mid+dis]$的点，即可找到是否存在小于dis距离的点对。
但是存在一个最坏情况，即通过左右两个区域计算得到的dis距离来划分的第三区域可能包含集合所有的点，这时候进行遍历查找，时间复杂度仍然和brute force方法相同，都为$O(n^2)$。因此需要对此进行深一步的考虑。
1985年Preparata和Shamos在给出该问题的一个分治算法并且还具体分析了在$[mid-dis,mid+dis]$区域中出现的情况，若（p,q）是Q的最近点对，p在带域左半部分，则q点必在下图所示的$\delta \ast 2\delta$长方形上，而在该长方形上，最多只能由右边点集的6个点。每个点对之间的距离不小于$\delta$。

此结论很好证明，通过在$\delta \ast 2\delta$上以$\frac{2\delta }{3}\ast \frac{\delta }{2}$划成6个小长方形

用反证法来证明，假设存在大于6个点，则必有一个或多个小长方形存在两个及以上点，而小长方形的最长距离是为对角线长度，为：$sqrt(\frac{2\delta }{3}\ast \frac{2\delta }{3}+\frac{\delta }{2}\ast \frac{\delta }{2})=\frac{5\delta }{6}<\delta$。最长距离都小于$\delta$，与之前的条件不符合，故最多有6个点。借此，可以将可能的线性时间缩小到常数级，大大提高了平均时间复杂度。
1998年，由周玉林、熊鹏荣、朱洪教授提出了平面最近点对的一个改进算法，针对Preparata-Shamos算法提出的6个点，又证明其实只需要4个点就可以确定最近点对距离，该证明提出2个定理，利用更加准确的半径画圈，证明了只要对左半域上的每个点p，检验右半域y坐标与p最近的至多4个点即可（上下个两个）。具体证明可以参考《求平面点集最近点对的一个改进算法》。
根据以上的优化，可以在合并时，通过检测与左半域点p的y坐标相邻的2个或者3个，即使用4点或者6点来检测，一般为了省事，只求与p点y坐标上界或者下界右半域连续的6个、4个点即可。

时间复杂度

在分解和合并时，可能存在按照x轴、y轴进行排序的预处理$O(nlogn)$，该问题在解决阶段只做提取的操作为$\Theta (n)$，递推式为：
$$T(n)=\{\begin{array}{ll}1& n<=3\\ 2T(\frac{n}{2})+O(n)& n>3\end{array}$$
计算后得到整体时间复杂度为：$O(nlogn)$

代码实现

struct point {
	double x;
	double y;
	point(double x, double y) :x(x), y(y) {}
	point() { return; }
};

bool cmp_x(const point & A, const point & B)  // 比较x坐标
{
	return A.x < B.x;
}

bool cmp_y(const point & A, const point & B)  // 比较y坐标
{
	return A.y < B.y;
}

double distance(const point & A, const point & B)
{
	return sqrt(pow(A.x - B.x, 2) + pow(A.y - B.y, 2));
}
/*
* function: 合并，同第三区域最近点距离比较
* param: points 点的集合
*        dis 左右两边集合的最近点距离
*        mid x坐标排序后，点集合中中间点的索引值
*/
double merge(vector<point> & points, double dis, int mid)
{
	vector<point> left, right;
	for (int i = 0; i < points.size(); ++i)  // 搜集左右两边符合条件的点
	{
		if (points[i].x - points[mid].x <= 0 && points[i].x - points[mid].x > -dis)
			left.push_back(points[i]);
		else if (points[i].x - points[mid].x > 0 && points[i].x - points[mid].x < dis)
			right.push_back(points[i]);
	}
	sort(right.begin(), right.end(), cmp_y);
	for (int i = 0, index; i < left.size(); ++i)  // 遍历左边的点集合，与右边符合条件的计算距离
	{
		for (index = 0; index < right.size() && left[i].y < right[index].y; ++index);
		for (int j = 0; j < 7 && index + j < right.size(); ++j)  // 遍历右边坐标上界的6个点
		{
			if (distance(left[i], right[j + index]) < dis)
				dis = distance(left[i], right[j + index]);
		}
	}
	return dis;
}


double closest(vector<point> & points)
{
	if (points.size() == 2) return distance(points[0], points[1]);  // 两个点
	if (points.size() == 3) return min(distance(points[0], points[1]), min(distance(points[0], points[2]), 
		distance(points[1], points[2])));  // 三个点
	int mid = (points.size() >> 1) - 1;
	double d1, d2, d;
	vector<point> left(mid + 1), right(points.size() - mid - 1);
	copy(points.begin(), points.begin() + mid + 1, left.begin());  // 左边区域点集合
	copy(points.begin() + mid + 1, points.end(), right.begin());  // 右边区域点集合
	d1 = closest(left);
	d2 = closest(right);
	d = min(d1, d2);
	return merge(points, d, mid);
}

int main()
{
	int count;
	printf("点个数：");
	scanf("%d", &count);
	vector<point> points;
	double x, y;
	for (int i = 0; i < count; ++i)
	{
		printf("第%d个点", i);
		scanf("%lf%lf", &x, &y);
		point p(x, y);
		points.push_back(p);
	}
	sort(points.begin(), points.end(), cmp_x);
	printf("最近点对值：%lf", closest(points));
	return 0;
}```