傅里叶变换基础

傅里叶变换基础

直观理解

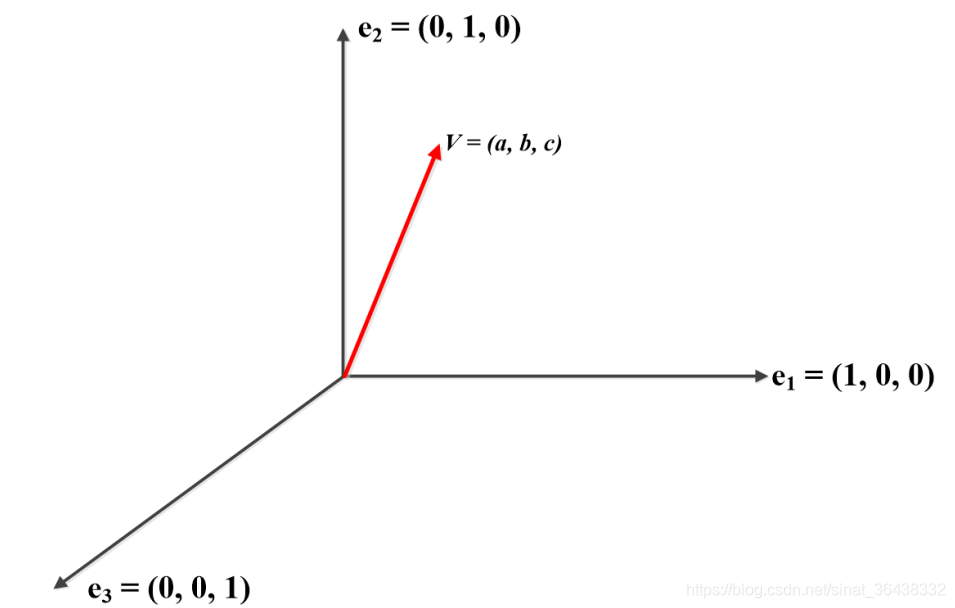
在如上图所示的三维坐标系中，向量v的坐标可以分解为向量v与三个基向量的内积：
$$a=\mathbf{v}\cdot {\mathbf{e}}_{1}b=\mathbf{v}\cdot {\mathbf{e}}_{2}c=\mathbf{v}\cdot {\mathbf{e}}_3$$
同时，向量v可以表示为三个基向量按照v的坐标的合成：
$$\mathbf{v}=a{\mathbf{e}}_1+b{\mathbf{e}}_2+c{\mathbf{e}}_3$$
因此，只要获得了坐标系的基向量，坐标系中任何向量分解与合成都可以利用基向量表示。基向量是一组线性无关的向量组，如上图的三个两两正交的向量。

直观上，傅里叶变换也是建立了一个坐标系，坐标系的基两两正交(这将在下面做出证明),任何一个信号都可以用这个坐标系中的基来进行分解与合成：

$e^{j\omega t}$即为这个坐标系下的基，不同ω下$e^{j\omega t}$两两正交(这将在下面做出证明)，与上面两个公式类似，信号可以按照下面公式进行分解与合成：

分解：
$$X(\omega )={\int }_{-\infty }^{+\infty }x(t)e^{j\omega t}dt={\int }_{-\infty }^{+\infty }x(t)e^{-j\omega t}dt$$
注意由于$e^{j\omega t}$是复指数，计算内积时应取共轭。

合成：
$$x(t)={\int }_{-\infty }^{+\infty }X(\omega )e^{j\omega t}d\omega$$

基本指数信号

我们分别约定ω和Ω分别代表连续时间域和离散时间域的频率。$e^{j\omega t}$和$e^{j\Omega t}$分别是连续时间域和离散时间域的指数信号，它们有着优秀的性质：

连续域指数信号$e^{j\omega t}$的性质

1.这是一个周期信号，最小周期T=2π/ω.由于$e^{2\pi j}=1$,所以周期性很容易看出来：
$$e^{j\omega t}=e^{j\omega (t+kT)}=e^{j\omega \left(t+k\frac{2\pi }{\omega }\right)}$$
根据上面的公式也不难看出来，ω越大，信号震荡的速率越高。

2.当$|{\omega }_1|$≠$|{\omega }_2|$时，$e^{j{\omega }_{1}t}$和$e^{j{\omega }_{2}t}$正交。这是一个很重要的性质，下面做一个简单的证明：

考虑到$e^{j\omega t}$是周期信号，我们只需要证明他们在一个相同的周期内正交。假设T是这两个信号最小周期T1、T2的最小公倍数(其中，$T_1=2\pi /{\omega }_1$,$T_2=2\pi /{\omega }_2$).
$$T=k_1{T}_1=k_1\frac{2\pi }{{\omega }_1}\text{ and }T=k_2{T}_2=k_2\frac{2\pi }{{\omega }_2}\left(k_1,k_2\in Z^{+}\right)$$
要证明这两个信号正交，只需证明它们的内积为0。需要注意的是这两个信号是复指数，因此计算内积时需要计算后一个信号的共轭：
$$\begin{array}{l}{\int }_0^T{e}^{j{\omega }_{1}t}{e}^{j{\omega }_{2}t}dt={\int }_0^T{e}^{j\left({\omega }_1-{\omega }_2\right)t}dt=\frac{1}{j\left({\omega }_1-{\omega }_2\right)}{e}^{j\left({\omega }_1-{\omega }_2\right)t}|\begin{array}{l}T\\ 0\end{array}\\ =\frac{1}{j\left({\omega }_1-{\omega }_2\right)}\left(e^{j\left(k_1-k_2\right)2\pi }-1\right)=0\end{array}$$
上面公式并不难，就不做详解了。

离散域指数信号$e^{j\Omega t}$的性质

1.并非对于所有的Ω来说，$e^{j\Omega t}$是周期信号。仅当Ω/2π是有理数(即Ω/2π=m/N)的时候，才是周期信号。这是因为当Ω/2π=m/N时，有：
$$e^{j\Omega n}=e^{j\Omega (n+N)}=e^{j(\Omega n+2\pi m)}$$
2.$e^{j\Omega t}$不是频率独立的(distinct)，这是因为$e^{j{\Omega }_{0}n}=e^{j({\Omega }_0\pm 2\pi k)n}$，所以${\Omega }_0$和$({\Omega }_0\pm 2\pi k)$对于信号的效果是一样的。

傅里叶变换的公式表示

通过上面的直观理解，我们可以给出傅里叶变化的公式：

信号分解：
$$X(\omega )={\int }_{-\infty }^{+\infty }x(t)e^{-j\omega t}dt$$
信号合成：
$$x(t)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }X(\omega )e^{j\omega t}d\omega$$
如果我们对信号的周期f更感兴趣，可以根据$f=2\pi /\omega$来用周期f代替频率ω：

信号分解：
$$X(f)={\int }_{-\infty }^{+\infty }x(t)e^{-j2\pi ft}dt$$
信号合成：
$$x(t)={\int }_{-\infty }^{+\infty }X(f)e^{j2\pi ft}df$$
一个信号存在傅里叶变换需要满足 狄利克雷条件，它是一个充分不必要条件：

1. 信号x(t)绝对可积。
   $${\int }_{-\infty }^{+\infty }|x(t)|dt<\infty$$

2. 在任何间隔内，信号x(t)的极大值和极小值的数目应是有限个。

3. 在任何间隔内，信号x(t)连续或只有有限个第一类间断点。

参考

中国大学慕课：数字图像处理与英语，浙江大学

A. V. Oppenheim, A. S. Willsky and I. T. Young,Signals and Systems, Prentice-Hall, 1983