电信保温杯笔记——《统计学习方法（第二版）——李航》第9章 EM算法及其推广

论文

EM算法：《Maximum Likelihood from Incomplete Data Via the EM Algorithm》
GEM算法：《A view of the EM algorithm that justifies incremental, sparse, and other variants》

介绍

电信保温杯笔记——《统计学习方法（第二版）——李航》
本文是对原书的精读，会有大量原书的截图，同时对书上不详尽的地方进行细致解读与改写。

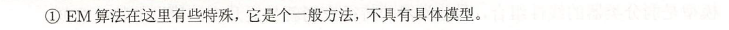
EM算法

原理：定义一个 $Q(\theta ,{\theta }^{(i)})$ 函数，求 $Q(\theta ,{\theta }^{(i)})$ 最大值时的 $\theta$，同时又令它为 ${\theta }^{(i+1)}$，并将 ${\theta }^{(i+1)}$ 带入 $Q$ 函数，再求 $Q(\theta ,{\theta }^{(i+1)})$ 最大值时的 $\theta$，经过多次迭代后，可得到 $P(y|\theta )$。

电信保温杯笔记——《统计学习方法（第二版）——李航》第4章 朴素贝叶斯法中的数学基础里，有最大后验概率估计和极大似然估计的解释。

下面例子中，$A,B,C,\pi ,p,q$ 就是隐藏变量，正反面就是观测值。每一个观测值只源于模型 B，C，而模型B，C 发生的只取决于A。

例子

步骤

$$\begin{array}{rl}Q(\theta ,{\theta }^{(i)})& =E_Z[\log P(Y,Z|\theta )|Y,{\theta }^{(i)}]\\ & =\sum _{Z}P(Z|Y,{\theta }^{(i)})\log P(Y,Z|\theta )(9.9)\end{array}$$

推导

$${\lambda }_j=P(Z|Y,{\theta }^{(i)}),y_j=\frac{P(Y|Z,\theta )P(Z|\theta )}{P(Z|Y,{\theta }^{(i)})}$$
$$\begin{array}{rl}L(\theta )-L({\theta }^{(i)})& =\log \left(\sum _{Z}P(Z|Y,{\theta }^{(i)})\frac{P(Y|Z,\theta )P(Z|\theta )}{P(Z|Y,{\theta }^{(i)})}\right)-\log P(Y|{\theta }^{(i)})\\ & \ge \sum _{Z}P(Z|Y,{\theta }^{(i)})\log \frac{P(Y|Z,\theta )P(Z|\theta )}{P(Z|Y,{\theta }^{(i)})}-\log P(Y|{\theta }^{(i)})\\ & =\sum _{Z}P(Z|Y,{\theta }^{(i)})\log \frac{P(Y|Z,\theta )P(Z|\theta )}{P(Z|Y,{\theta }^{(i)})}-\sum _{Z}P(Z|Y,{\theta }^{(i)})\log P(Y|{\theta }^{(i)})\\ & =\sum _{Z}P(Z|Y,{\theta }^{(i)})\log \frac{P(Y|Z,\theta )P(Z|\theta )}{P(Z|Y,{\theta }^{(i)})P(Y|{\theta }^{(i)})}\end{array}$$

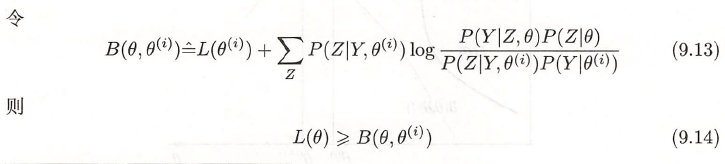
$$\begin{array}{rl}Q(\theta ,{\theta }^{(i)})& =E_Z[\log P(Y,Z|\theta )|Y,{\theta }^{(i)}]\\ & =\sum _{Z}P(Z|Y,{\theta }^{(i)})\log P(Y,Z|\theta )(9.9)\end{array}$$

收敛性

感觉这一部分可以不用看，直接看GEM算法。

GEM算法

高斯混合模型

${\alpha }_k,{\sigma }_k$ 决定每个高斯模型的高矮肥瘦。

使用EM算法估计高斯混合模型的参数

1. 明确隐变量,写出完全数据的对数似然函数

$$\begin{array}{rl}P(y,\gamma |\theta )& =\prod _{j=1}^{N}P(y_j,{\gamma }_{j1},{\gamma }_{j2},\cdots ,{\gamma }_{jK}|\theta )\\ & =\prod _{j=1}^N\prod _{k=1}^K[{\alpha }_k{\varphi }_k(y_j|{\theta }_k){]}^{{\gamma }_{jk}}\\ & =\prod _{k=1}^K\prod _{j=1}^N{\alpha }_k^{{\gamma }_{jk}}[{\varphi }_k(y_j|{\theta }_k){]}^{{\gamma }_{jk}}\\ & =\prod _{k=1}^K{\alpha }_k^{\sum _{j=1}^N{\gamma }_{jk}}\prod _{j=1}^N[{\varphi }_k(y_j|{\theta }_k){]}^{{\gamma }_{jk}}\end{array}$$
那么,完全数据的对数似然函数为

$$\begin{array}{rl}\log P(y,\gamma |\theta )& =\log \left[\prod _{k=1}^K{\alpha }_k^{\sum _{j=1}^N{\gamma }_{jk}}\prod _{j=1}^N[{\varphi }_k(y_j|{\theta }_k){]}^{{\gamma }_{jk}}\right]\\ & =\sum _{k=1}^K\left\{\sum _{j=1}^N{\gamma }_{jk}\log {\alpha }_k+\sum _{j=1}^N{\gamma }_{jk}\left[\log \left(\frac{1}{\sqrt{2\pi }}\right)-\log {\sigma }_k-\frac{1}{2{\sigma }_k^2}(y_j-{\mu }_k{)}^2)\right]\right\}\end{array}$$

2. EM算法的E步:确定Q函数

$$\begin{array}{rl}Q(\theta ,{\theta }^{(i)})& =E_Z[\log P(Y,Z|\theta )|Y,{\theta }^{(i)}]\\ & =\sum _{Z}P(Z|Y,{\theta }^{(i)})\log P(Y,Z|\theta )(9.9)\end{array}$$
$$Z=\gamma$$
$$\begin{array}{rl}Q(\theta ,{\theta }^{(i)})& =E[\log P(y,\gamma |\theta )|y,{\theta }^{(i)}]\\ & =E\left\{\sum _{k=1}^K\left\{\sum _{j=1}^N{\gamma }_{jk}\log {\alpha }_k+\sum _{j=1}^N{\gamma }_{jk}\left[\log \left(\frac{1}{\sqrt{2\pi }}\right)-\log {\sigma }_k-\frac{1}{2{\sigma }_k^2}(y_j-{\mu }_k{)}^2)\right]\right\}\right\}\\ & =\sum _{k=1}^K\left\{\log {\alpha }_k\sum _{j=1}^N(E{\gamma }_{jk})+\sum _{j=1}^N(E{\gamma }_{jk})\left[\log \left(\frac{1}{\sqrt{2\pi }}\right)-\log {\sigma }_k-\frac{1}{2{\sigma }_k^2}(y_j-{\mu }_k{)}^2)\right]\right\}(9.28)\end{array}$$

这里需要计算 $E({\gamma }_{jk}|y,{\theta }^{(i)})$，记为 ${\hat{\gamma }}_{jk}$。
$$\begin{array}{rl}{\hat{\gamma }}_{jk}& =E({\gamma }_{jk}|y,{\theta }^{(i)})=P({\gamma }_{jk}=1|y,{\theta }^{(i)})\cdot 1+P({\gamma }_{jk}=0|y,{\theta }^{(i)})\cdot 0\\ & =P({\gamma }_{jk}=1|y,{\theta }^{(i)})\\ & =\frac{P({\gamma }_{jk}=1,y_j|{\theta }^{(i)})}{P(y_j|{\theta }^{(i)})}\\ & =\frac{P({\gamma }_{jk}=1,y_j|{\theta }^{(i)})}{\sum _{k=1}^{K}P({\gamma }_{jk}=1,y_j|{\theta }^{(i)})}\text{（分母为互斥事件）}\\ & =\frac{P({\gamma }_{jk}=1|{\theta }^{(i)})P(y_j|{\gamma }_{jk}=1,{\theta }^{(i)})}{\sum _{k=1}^{K}P({\gamma }_{jk}=1|{\theta }^{(i)})P(y_j|{\gamma }_{jk}=1,{\theta }^{(i)})}\\ & =\frac{{\alpha }_k^{(i)}\varphi (y_j|{\theta }_k^{(i)})}{\sum _{k=1}^K{\alpha }_k^{(i)}\varphi (y_j|{\theta }_k^{(i)})},j=1,2,\cdots ,N;k=1,2,\cdots ,K\end{array}$$
令
$$n_k=\sum _{j=1}^N{\gamma }_{jk}=\sum _{j=1}^{N}E{\gamma }_{jk}$$

3. 确定EM算法的M步

${\theta }_k=({\alpha }_k,{\mu }_k,{\sigma }_k)$

$$\begin{array}{rl}\frac{\partial Q(\theta ,{\theta }^{(i)})}{\partial {\mu }_k}& =\frac{\partial \left\{\sum _{k=1}^K\left\{n_k\log {\alpha }_k+\sum _{j=1}^N{\hat{\gamma }}_{jk}\left[\log \left(\frac{1}{\sqrt{2\pi }}\right)-\log {\sigma }_k-\frac{1}{2{\sigma }_k^2}(y_j-{\mu }_k{)}^2)\right]\right\}\right\}}{\partial {\mu }_k}\\ & =\sum _{j=1}^N{\hat{\gamma }}_{jk}\left(-\frac{1}{2{\sigma }_k^2}\cdot 2({\mu }_k-y_j)\right)\\ & =-\frac{1}{{\sigma }_k^2}\sum _{j=1}^N{\hat{\gamma }}_{jk}({\mu }_k-y_j)\\ & =\frac{1}{{\sigma }_k^2}\sum _{j=1}^N{\hat{\gamma }}_{jk}(y_j-{\mu }_k)\\ & =\frac{1}{{\sigma }_k^2}(\sum _{j=1}^N{\hat{\gamma }}_{jk}{y}_j-{\mu }_k\sum _{j=1}^N{\hat{\gamma }}_{jk})\\ & =0\end{array}$$
$${\hat{\mu }}_k={\mu }_k^{(i+1)}=\frac{\sum _{j=1}^N{\hat{\gamma }}_{jk}{y}_j}{\sum _{j=1}^N{\hat{\gamma }}_{jk}},k=1,2,\cdots ,K$$
$$\begin{array}{rl}\frac{\partial Q(\theta ,{\theta }^{(i)})}{\partial {\sigma }_k^2}& =\frac{\partial \left\{\sum _{k=1}^K\left\{n_k\log {\alpha }_k+\sum _{j=1}^N{\hat{\gamma }}_{jk}\left[\log \left(\frac{1}{\sqrt{2\pi }}\right)-\log {\sigma }_k-\frac{1}{2{\sigma }_k^2}(y_j-{\mu }_k{)}^2)\right]\right\}\right\}}{\partial {\sigma }_k^2}\\ & =\frac{\partial \left\{\sum _{k=1}^K\left\{n_k\log {\alpha }_k+\sum _{j=1}^N{\hat{\gamma }}_{jk}\left[\log \left(\frac{1}{\sqrt{2\pi }}\right)-\frac{1}{2}\log {\sigma }_k^2-\frac{1}{2{\sigma }_k^2}(y_j-{\mu }_k{)}^2)\right]\right\}\right\}}{\partial {\sigma }_k^2}\\ & =\sum _{j=1}^N{\hat{\gamma }}_{jk}\left(-\frac{1}{2{\sigma }_k^2}+\frac{1}{2{\sigma }_k^4}\cdot ({\mu }_k-y_j{)}^2\right)\\ & =-\frac{1}{2{\sigma }^4}\sum _{j=1}^N{\hat{\gamma }}_{jk}\left({\sigma }_k^2-({\mu }_k-y_j{)}^2\right)\\ & =-\frac{1}{2{\sigma }^4}\left({\sigma }_k^2\sum _{j=1}^N{\hat{\gamma }}_{jk}-\sum _{j=1}^N{\hat{\gamma }}_{jk}({\mu }_k-y_j{)}^2\right)\\ & =0\end{array}$$
$${\hat{\sigma }}_k^2={\sigma }_k^{2(i+1)}=\frac{\sum _{j=1}^N{\hat{\gamma }}_{jk}({\mu }_k-y_j{)}^2}{\sum _{j=1}^N{\hat{\gamma }}_{jk}},k=1,2,\cdots ,K$$

使用拉格朗日函数：
$$\begin{array}{rl}\frac{\partial \left\{Q(\theta ,{\theta }^{(i)})+\lambda (1-\sum _{k=1}^K{\alpha }_k)\right\}}{\partial {\alpha }_k}& =\frac{\partial \left\{\sum _{k=1}^K\left\{n_k\log {\alpha }_k+\sum _{j=1}^N{\hat{\gamma }}_{jk}\left[\log \left(\frac{1}{\sqrt{2\pi }}\right)-\log {\sigma }_k-\frac{1}{2{\sigma }_k^2}(y_j-{\mu }_k{)}^2)\right]\right\}+\lambda (1-\sum _{k=1}^K{\alpha }_k)\right\}}{\partial {\alpha }_k}\\ & =n_k\frac{1}{{\alpha }_k}-\lambda \\ & =0\end{array}$$
$$\begin{array}{rl}\frac{\partial \left\{Q(\theta ,{\theta }^{(i)})+\lambda (1-\sum _{k=1}^K{\alpha }_k)\right\}}{\partial \lambda }& =\frac{\partial \left\{\sum _{k=1}^K\left\{n_k\log {\alpha }_k+\sum _{j=1}^N{\hat{\gamma }}_{jk}\left[\log \left(\frac{1}{\sqrt{2\pi }}\right)-\log {\sigma }_k-\frac{1}{2{\sigma }_k^2}(y_j-{\mu }_k{)}^2)\right]\right\}+\lambda (1-\sum _{k=1}^K{\alpha }_k)\right\}}{\partial \lambda }\\ & =1-\sum _{k=1}^K{\alpha }_k\\ & =0\end{array}$$

$${\hat{\alpha }}_k={\alpha }_k^{(i+1)}=\frac{n_k}{\lambda }=\frac{n_k}{\sum _{k=1}^K{n}_k}=\frac{n_k}{N}=\frac{\sum _{j=1}^N{\hat{\gamma }}_{jk}}{N},k=1,2,\cdots ,K$$

步骤

EM算法的推广

F函数的极大-极大算法

GEM算法

GEM算法1

GEM算法2

GEM算法3

本章概要

备注

EM算法的推广这部分还没看，日后用到再回来细看。

相关视频

相关的笔记

hktxt /Learn-Statistical-Learning-Method

相关代码

Dod-o /Statistical-Learning-Method_Code
关于def loadData(mu0, sigma0, mu1, sigma1, alpha0, alpha1):
以概率 ${\alpha }_k$ 使第 $k$ 个高斯模型生成数据 $y_j$。并不像之前几个模型那样使用图像数据集。

关于def calcGauss(dataSetArr, mu, sigmod):
计算

pytorch

tensorflow

keras

pytorch API:

tensorflow API