Chapter 3 Classification （mnist数据集）

设置

from __future__ import division,print_function,unicode_literals
import numpy as np
np.random.seed(42)

%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12

import os
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "classification"
def save_fig(fig_id,tight_layout = True):
    path = os.path.join(PROJECT_ROOT_DIR,"images",CHAPTER_ID,fig_id + ".png")
    print("Saving figure",fig_id)
    if tight_layout:
        plt.tight_layout()
    plt.saving(path,format = 'png',dpi = 300)

import warnings
warnings.filterwarnings(action = "ignore",message = "^internal gelsd")

获取数据

from sklearn.datasets import fetch_mldata
mnist = fetch_mldata('MNIST original')
minst

输出错误 

警告:自从Scikit-Learn 0.20以来，fetch_mldata()就被弃用了。您应该使用fetch_openml()。但是，它返回未排序的MNIST数据集，而fetch_mldata()返回按目标排序的数据集(训练集和测试集分别排序)。一般来说，这是好的，但如果你想要得到与之前完全相同的结果，需要对数据集进行排序。（按照标签值进行排序0，1，……，8，9）

def sort_by_target(mnist):
    reorder_train = np.array(sorted([(target,i) for i,target in enumerate(mnist.target[:60000])]))[:,1]
    recoder_test = np.array(sorted([(target,i) for i,target in enumerate(mnist.target[60000:])]))[:,1]
    mnist.data[:60000] = mnist.data[recoder_train]
    mnist.target[:60000] = mnist.target[recoder_train]
    mnist.data[60000:] = mnist.data[recoder_test + 60000]
    mnist.target[60000:] = mnist.target[recoder_test + 60000]
try:
    from sklearn.datasets import fetch_openml
    mnist = fetch_openml('mnist_784',version = 1,cache = True)
    mnist.target = mnist.target.astype(np.int8)
    sort_by_target(mnist)
except:
    from sklearn.datasets import fetch_mldata
    mnist = fetch_mldata('MNIST original')

mnist["data"],mnist["target"]

mnist.data.shape

MNIST一共有70000条数据，每条数据有784个特征（每张图片都是28 x 28像素的）。

X,y = mnist["data"],mnist["target"]
X.shape,y.shape

  

随便看一下其中一条数据中的数字

%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
some_digit = X[36000]
some_digit_image = some_digit.reshape(28,28)
plt.imshow(some_digit_image,cmap = matplotlib.cm.binary,interpolation = "nearest")
plt.axis("off")
save_fig("some_digit_plot")
plt.show()

y[36000]

更加直观的感受一下数据集

def plot_digit(data):
    image = data.reshape(28,28)
    plt.imshow(image,cmap = matplotlib.cm.binary,interpolation = "nearest")
    plt.axis("off")

def plot_digits(instances,images_per_row = 10,**options):
    size = 28
    images_per_row = min(len(instances),image_per_row)
    images = [instance.reshape(size,size) for instance in instances]
    n_rows = (len(instances) - 1) // images_per_row + 1
    row_images = []
    n_empty = n_rows * images_per_row - len(instances)
    images.append(np.zeros((size,size * n_empty)))
    for row in range(n_rows):
        rimages = images[row * images_per_row : (row + 1) * images_per_row]
        row_images.append(np.concatenate(rimages,axis = 1))
    image = np.concatenate(row_images,axis = 0)
    plt.imshow(image,cmap = matplotlib.cm.binary, **options)
    plt.axis("off")

plt.figure(figuresize = (9,9))
example_images = np.r_[X[:12000:600],X[13000:30600:600],X[30600:60000:590]]
plot_digits(example_images,images_per_row = 10)
save_fig("more_digits_plot")
plt.show()

MNIST已经把测试集做好了。前面60000个当作训练集，后面10000个当测试集。

X_train,X_test,y_rain,y_test = X[:60000],X[60000:],y[:60000],y[60000:]
import numpy as np
shuffle_index = np.random.permutation(60000)
X_train,y_train = X_train[shuffle_index],y_train[shuffle_index]

MNIST的数据是按数字大小顺序排列的，所以先要打乱它的顺序，这样可以保证交叉验证在每一次都是相似的。

训练一个二分类器

先不做一个多类器，我们不去识别里面的手写数字是0~9中的某一个数。目前做一个最简单的，判断它是否是5，即将数据分成两个类别：“5”和“非5”。(# 这是一个逻辑数组，5：True, 非5：False)

y_train_5 = (y_train == 5)
y_test_5 = (y_test == 5)

from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(max_iter = 5,rabdom_state = 42)
sgd_clf.fit(X_train,y_train_5)

收敛警告:在收敛之前达到的最大迭代次数。考虑增加max_iter来改善配合。

from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(max_iter = 5,tol = -np.infty,rabdom_state = 42)
sgd_clf.fit(X_train,y_train_5)

sgd_clf.predict([some_digit])

从输出的结果True可以看出来，这个模型预测正确了，确实是个5，看起来还不错。

对性能的评估

下面来整体评估一下这个分类的性能。上面只是让模型预测了一个数字，并不能代表什么，说不定是那个模型运气好，猜中了。接下来得整体看一下它的准确率，这样子才有说服力。

1.使用交叉验证测量准确性

from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf,X_train,y_train_5,cv = 3,scoring = "accuracy")  

注： StratfiedKFold 类实现了分层采样，生成的折包含了各类相应比例的样例。在每一次迭代，上述代码生成分类器的一个克隆，在克隆的模型上训练，在测试折上进行预测 。

from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone
skfolds = StratifiedKFold(n_splits = 3,random_state = 42)
for train_index,test_index in skfolds.split(X_train,y_train_5):
    clone_clf = clone(sgd_clf)
    X_train_folds = X_train[train_index]
    y_train_folds = (y_train_5[train_index])
    X_test_fold = X_train[test_index]
    y_train_fold = (y_train_5[test_index])
    clone_clf.fit(X_train_folds,y_train_folds)
    y_pred = clone_clf.predict(X_test_fold)
    n_correct = sum(y_pred == y_test_fold)
    print(n_correct / len(y_pred))  

再来看下一个非常简单的分类器去分类，看看它在“非5”这个类上的表现。这个分类器就是，不管青红皂白，都认为这个数字不是5，即将它归为非5。

from sklearn.base import BaseEstimator
class Never5Classifier(BaseEstimator):
    def fit(self,X,y = None):
        pass
    def predict(self,X):
        return np.zeros((len(X),1), dtype = bool)

never_5_clf = Never5Classifier()
cross_val_score(never_5_clf,X_train,y_train_5,cv = 3,scoring = "accuracy")  

因为只有10%的样本是5，其它都是非5，所以只要一直猜这个图像不是5，当然有90%的精度，这叫数据不平衡。所以精度并不是一个好的性能度量指标，特别是在我们数据不平衡的时候。

2.混淆矩阵

对一般分类器来说，比较好的性能评估指标是混淆矩阵。大体思路是：输出类别A被分成类别B的次数。

为了计算混淆矩阵，首先你需要有一系列的预测值，这样才能将预测值与真实值做比较。你或许想在测试集上做预测。

cross_val_predict与cross_val_score一样都是K折交叉验证，前者返回基于每个测试折做出的预测值，后者返回的是评估分数。

from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf,X_train,y_train_5,cv = 3)

from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5,y_train_pred)

混淆矩阵中的每一行表示一个实际的类，而每一列表一个预测的类。该矩阵的第一行认为"非5"中的53417张被正确地归类为非5（这被称为真反例，true negatives）,而其余1162被错误归类为5（这被称为假正例，false positives），第二行认为"5"中的1350张被错误地归类为非5（这被称为假反例，false negatives），4071正确分类为"5"类（真正例，true positive）。一个完美的分类器将只有真反例和真正例，所混淆矩阵的非零值仅在其主对角线（左上至右下）。

y_train_perfect_predictions = y_train_5
confusion_matrix(y_train_5,y_train_perfect_pedictions)

混淆矩阵可以提供很多信息。有时候你会想要更加简明的指标。一个有趣的指标是正例预测的精度，也叫做分类器的准确率(precision)。

其中TP是真正例的数目，FP是假正例的数目。

准确率一般会伴随另一个指标一起使用，这个指标叫做召回率（recall），也叫做敏感度（sensitivity）或者真正例率（true positive rate, TPR）。这是正例被分类器正确探测出的比率。

FN是假反例的数目。

from sklearn.metrics import precision_score,recall_score
precision_socre(y_train_5,y_train_pred)

4344 / (4344 + 1307)

recall_socre(y_train_5,y_train_pred)

4344 / (4344 + 1077)

通常结合准确率和召回率会更加方便，这个指标叫做F1值，特别是当你需要一个简单的方法去比较两个分类器的优劣的时时候。F1值是准确率和召回率的调和平均。

计算F1值，简单调用f1_score()即可。

from sklearn.metrics import f1_score
f1_score(y_train_5,y_train_pred) 

4344 / (4344 + (1077 + 1307) / 2)

F1支持那些有着相近准确率和召回率的分类（意思是只有当准确率和召回率一样大时，F1值才会大）。但并不是所有时候，我们都关心F1值，有时候我们只关心准确率（precision），或者有时候我们只关心召回率（recall）。

再次理解一下准确率的含义：如果一个分类器每次几乎都能把所要分的类别准确地分类出来，那么无疑，这个分类器的准确率是高的；什么时候准确率低呢，就是它把所要分的类预测错了。比如，要预测这张手写图片的数字是否是5，如果那张图真的是5，而我们的分类器预测它是5，那么它预测对了。

什么是召回率？当将一张是5的图片预测成不是5，说明这个分类器还是比较严格的，那它有较低的召回率。

总的来说，准确率低的原因就产将那些看起来像5（只是像，实际并不是5）的预测成了5；而召回率低的原因是把那些看起来不像5（实际上是5，只是可能那个5写得比较丑）预测成不是5。

在这里，举两个例子，比如公司想找个人当总经理，有一群人来应聘它。我们这时候的目标是，找到的这个人肯定是能够当总经理的，就算有的人看起来像是能当总经理，但是为了确保万无一失，我们要找一个看起来非常非常像能够当总经理的人。这个时候我们当然有着很高的准确率，因为我们找的人几乎肯定是能够当总经理的，但是此时，我们会犯另一个错误，就是有些人确实有能力当总经理，只是我们没有看出来（人不可貌像），所以我们拒绝他，因此我们有低的召回率，这在统计学上被称为犯了第一类错误，即弃真。这样做是合理的，因为即使弃真，但我们保真了。

另一种情况是，比如警察在一群人中想找出几个犯罪的人，这个时候我们就不能要超高的准确率了，因为有可能把真正的犯人放走。找犯人的原则一般是，只要他看起来像个犯人，都应该审查一下，即使最后真像大白后，他真的不是一个犯人。我们平时听到的宁可错杀一千，不可放走一个说的就是这个道理，因此这有着比较低的准确率，但是有高的召回率，这在统计学上被称为犯了第二类错误，即取伪。 

（1）准确率与召回率之间的折衷

Scikit-Learn 不让你直接设置阈值，但是它给你提供了设置决策分数的方法，这个决策分数可以用来产生预测。它不是调用分类器的predict()方法，而是调用decision_function()方法。这个方法返回每一个样例的分数值，然后基于这个分数值，使用你想要的任何阈值做出预测。

y_scores = sgd_clf.decision_function([some_digit])
y_scores

threshold = 0
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred

threshold = 200000
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred

这证明了提高阈值会降调召回率。这个图片实际就是数字 5，当阈值等于 0 的时候，分类器可以探测到这是一个 5，当阈值提高到 20000 的时候，分类器将不能探测到这是数字 5。

那么，你应该如何使用哪个阈值呢？首先，你需要再次使用cross_val_predict()得到每一个样例的分数值，但是这一次指定返回一个决策分数，而不是预测值。

y_scores = cross_val_predict(sgd_clf,X_train,y_train_5,cv = 3,method = "decision_function")

注意:在Scikit-Learn 0.19.0中有一个问题(修复于0.19.1中)，当使用method="decision_function"时，cross_val_predict()的结果在二进制分类的情况下是不正确的，如上面的代码所示。结果的数组有一个额外的充满0的第一个维度。如果你用的是0.19.0，我们需要增加这个小技巧来解决这个问题:

y_scores.shape

#在Scikit-Learn 0.19.0中，破解关于第9589期的问题
if y_scores.ndim == 2:
    y_scores = y_scores[:,1]

现在有了这些分数值。对于任何可能的阈值，使用precision_recall_curve(),你都可以计算准确率和召回率:

from sklearn.metrics import precision_recall_curve
precisions,recalls,thresholds = precision_recall_curve(y_train_5,y_scores)

最后，可以使用 Matplotlib 画出准确率和召回率，这里把准确率和召回率当作是阈值的一个函数。

def plot_precision_recall_vs_threshold(precisions,recalls,thresholds):
    plt.plot(thresholds,precisions[:-1],"b--",label = "Precision",linewidth = 2)
    plt.plot(thresholds,recalls[:-1],"g-",label = "Recall",linewidth = 2)
    plt.xlabel("Threshold",fontsize = 16)
    plt.legend(loc = "upper left",fontsize = 16)
    plt.ylim([0,1])

plt.figure(figsize = (8,4))
plot_precision_recall_vs_threshold(precisions,recalls,thresholds)
plt.xlim([-700000,700000])
save_fig("precision_recall_vs_threshold_plot")
plt.show()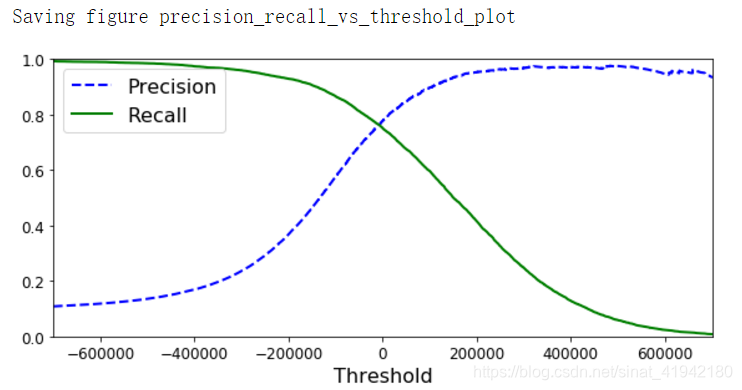

笔记：你也许会好奇为什么准确率曲线比召回率曲线更加起伏不平。原因是准确率有时候会降低，尽管当你提高阈值的时候，通常来说准确率会随之提高。另一方面，当阈值提高时候，召回率只会降低。这也就说明了为什么召回率的曲线更加平滑。

(y_train_pred == (y_scores > 0)).all()

假设你决定达到 90% 的准确率。你查阅第一幅图（放大一些），在 70000 附近找到一个阈值。为了作出预测（目前为止只在训练集上预测），你可以运行以下代码，而不是运行分类器的predict()方法。并检查这些预测的准确率和召回率：

y_train_pred_90 = (y_scores > 70000)
precision_score(y_train_5,y_train_pred_90)
recall_score(y_train_5,y_train_pred_90)

,  

很棒！你拥有了一个（近似） 90% 准确率的分类器。它相当容易去创建一个任意准确率的分类器，只要将阈值设置得足够高。但是，一个高准确率的分类器不是非常有用，如果它的召回率太低！

如果有人说“让我们达到 99% 的准确率”，你应该问“相应的召回率是多少？”

 另一个选出好的准确率/召回率折衷的方法是直接画出准确率对召回率的曲线。

def plot_precision_vs_recall(precisions,recalls):
    plt.plot(recalls,precisions,"b-",linewidth = 2)
    plt.xlabel("Recall",fontsize = 16)
    plt.ylabel("Precision",fontsize = 16)
    plt.axis([0,1,0,1])

plt.figure(figsize = (8,6))
plot_precision_vs_recall(precisions,recalls)
save_fig("precision_vs_recall_plot")
plt.show()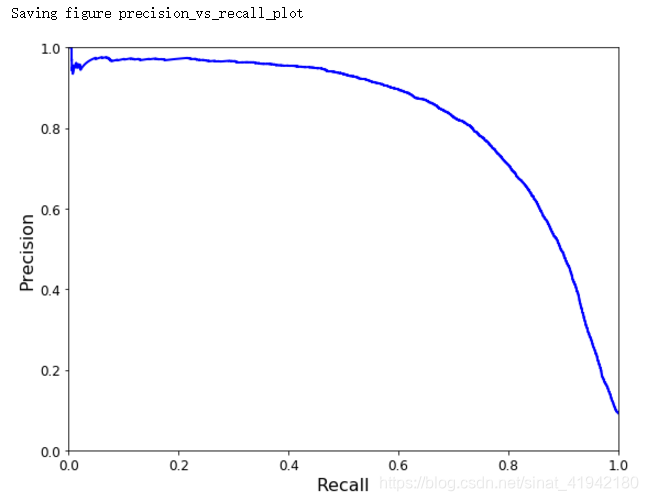

可以看到，在召回率在 80% 左右的时候，准确率急剧下降。你可能会想选择在急剧下降之前选择出一个准确率/召回率折衷点。比如说，在召回率 60% 左右的点。当然，这取决于你的项目需求。

（2）ROC曲线

ROC曲线是另一个二分类器常用的工具。它非常类似于准确率/召回率曲线，但不是画出准确率对召回率的曲线，ROC 曲线是真正例率（true positive rate，另一个名字叫做召回率）对假正例率（false positive rate, FPR）的曲线。FPR 是反例被错误分成正例的比率。它等于 1 减去真反例率（true negative rate， TNR）。TNR是反例被正确分类的比率。TNR也叫做特异性。所以 ROC 曲线画出召回率对（1 减特异性）的曲线。

为了画出 ROC 曲线，首先需要计算各种不同阈值下的 TPR、FPR，使用roc_curve()函数：

from sklearn.metrics import roc_curves
fpr,tpr,thresholds = roc_curve(y_train_5,y_scores)

然后使用 matplotlib，画出 FPR 对 TPR 的曲线。

def plot_roc_curve(fpr,tpr,label = None):
    plt.plot(fpr,tpr,linewidth = 2,label = label)
    plt.plot([0,1],[0,1],'k--')
    plt.axis([0,1,0,1])
    plt.xlabel('False Positive Rate',fontsize = 16)
    plt.ylabel('True Positive Rate',fontsize = 16)

plt.figure(figsize = (8,6))
plt_roc_curve(fpr,tpr)
save_fig("roc_curve_plot")
plt.show()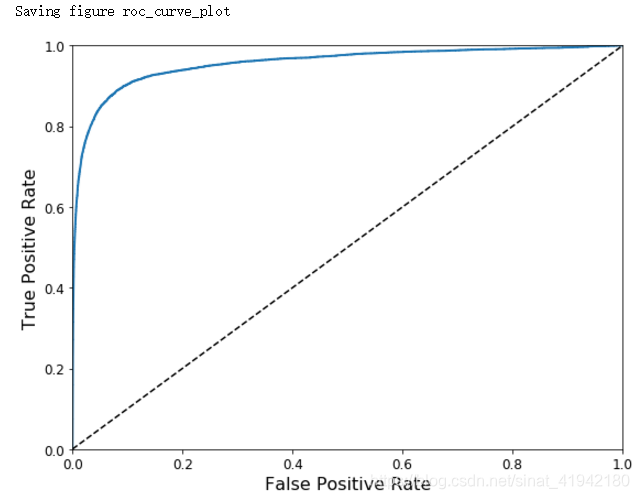

这里同样存在折衷的问题：召回率（TPR）越高，分类器就会产生越多的假正例（FPR）。图中的点线是一个完全随机的分类器生成的 ROC 曲线；一个好的分类器的 ROC 曲线应该尽可能远离这条线（即向左上角方向靠拢）。

一个比较分类器优劣的方法是：测量ROC曲线下的面积（AUC，area under the curve）。一个完美的分类器的 ROC AUC 等于 1，而一个纯随机分类器的 ROC AUC 等于 0.5。Scikit-Learn 提供了一个函数来计算 ROC AUC：

from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5,y_scores)

因为 ROC 曲线跟准确率/召回率曲线（或者叫 PR）很类似，你或许会好奇如何决定使用哪一个曲线呢？一个笨拙的规则是，当正例很少，或者当你关注假正例多于假反例的时候，优先使用 PR 曲线。其他情况使用 ROC 曲线。

训练一个RandomForestClassifier，然后拿它的的ROC曲线和ROC AUC数值去跟SGDClassifier的比较。首先你需要得到训练集每个样例的数值。但是由于随机森林分类器的工作方式，RandomForestClassifier不提供decision_function()方法。相反，它提供了predict_proba()方法。Skikit-Learn分类器通常二者中的一个。predict_proba()方法返回一个数组，数组的每一行代表一个样例，每一列代表一个类。数组当中的值的意思是：给定一个样例属于给定类的概率。比如，70%的概率这幅图是数字 5。

from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(n_estimator = 10,random_state = 42)
y_probas_forest = cross_val_predict(forest_clf,X_train,y_train_5,cv = 3,method = "predict_proba")

但是要画 ROC 曲线，你需要的是样例的分数，而不是概率。一个简单的解决方法是使用正例的概率当作样例的分数。

y_scores_forest = y_probs_forest[:,1]
fpr_forest,tpr_forest,threshold_forest = roc_curve(y_train_5,y_scores_forest)

现在你即将得到 ROC 曲线。将前面一个分类器的 ROC 曲线一并画出来是很有用的，可以清楚地进行比较。

plt.figure(figsize = (8,6))
plt.plot(fpr,tpr,"b:",linewidth = 2,label = "SGD")
plt_roc_curve(fpr_forest,tpr_forest,"Random Forest")
plt.legend(loc = "lower right",fontsize = 16)
save_fig("roc_curve_comparison_plot")
plt.show()

可知，RandomForestClassifier的 ROC 曲线比SGDClassifier的好得多：它更靠近左上角。所以，它的 ROC AUC 也会更大。

roc_auc_score(y_train_5, y_scores_forest)

y_train_pred_forest = cross_val_predict(forest_clf,X_train,y_train_5,cv = 3)
precision_score(y_train_5,y_train_pred_forest)​
recall_score(y_train_5,y_train_pred_forest)

, 

现在知道如何训练一个二分类器，选择合适的标准，使用交叉验证去评估分类器，选择满足需要的准确率/召回率折衷方案，和比较不同模型的 ROC 曲线和 ROC AUC 数值。下面将检测更多的数字，而不仅仅是一个数字 5。

多类分类

一些算法（比如随机森林分类器或者朴素贝叶斯分类器）可以直接处理多类分类问题。其他一些算法（比如 SVM 分类器或者线性分类器）则是严格的二分类器。然后，有许多策略可以让你用二分类器去执行多类分类。

举例子，创建一个可以将图片分成 10 类（从 0 到 9）的系统的一个方法是：训练10个二分类器，每一个对应一个数字（探测器 0，探测器 1，探测器 2，以此类推）。然后当你想对某张图片进行分类的时候，让每一个分类器对这个图片进行分类，选出决策分数最高的那个分类器。这叫做“一对所有”（OvA）策略”（也被叫做“一对其他”）。

另一个策略是对每一对数字都训练一个二分类器：一个分类器用来处理数字 0 和数字 1，一个用来处理数字 0 和数字 2，一个用来处理数字 1 和 2，以此类推。这叫做“一对一”（OvO）策略。如果有 N 个类。你需要训练N*(N-1)/2个分类器。对于 MNIST 问题，需要训练 45 个二分类器！当你想对一张图片进行分类，你必须将这张图片跑在全部45个二分类器上。然后看哪个类胜出。OvO 策略的主要优点是：每个分类器只需要在训练集的部分数据上面进行训练。这部分数据是它所需要区分的那两个类对应的数据。

一些算法（比如 SVM 分类器）在训练集的大小上很难扩展，所以对于这些算法，OvO 是比较好的，因为它可以在小的数据集上面可以更多地训练。但是，对于大部分的二分类器来说，OvA 是更好的选择。

Scikit-Learn 可以探测出你想使用一个二分类器去完成多分类的任务，它会自动地执行 OvA（除了 SVM 分类器，它使用 OvO）。试一下SGDClassifier.

sgd_clf.fit(X_train,y_train)
sgd_clf.predict([some_digit])

很容易。上面的代码在训练集上训练了一个SGDClassifier。在幕后，Scikit-Learn 实际上训练了 10 个二分类器，每个分类器都产到一张图片的决策数值，选择数值最高的那个类。为了证明这是真实的，调用decision_function()方法。不是返回每个样例的一个数值，而是返回 10 个数值，一个数值对应于一个类。

some_digit_scores = sgd_clf.decision_function([some_digit])
some_digit_scores

np.argmax(some_digit_scores)

最高数值是对应于的位置索引值为5 

sgd_clf.classes_
sgd_clf.classes_[5]

 ,

一个分类器被训练好了之后，它会保存目标类别列表到它的属性classes_ 中去，按照值排序。在本例子当中，在classes_ 数组当中的每个类的索引方便地匹配了类本身，比如，索引为 5 的类恰好是类别 5 本身。但通常不会这么幸运。

如果想强制 Scikit-Learn 使用 OvO 策略或者 OvA 策略，可以使用OneVsOneClassifier类或者OneVsRestClassifier类。创建一个样例，传递一个二分类器给它的构造函数。举例子，下面的代码会创建一个多类分类器，使用 OvO 策略，基于SGDClassifier。

from sklearn.multiclass import OneVsOneClassifier
ovo_clf = OneVsOneClassifier(SGDClassifier(max_iter = 5,tol = -np.infty,random_state = 42))
ovo_clf.fit(X_train,y_train)
ovo_clf.predict([some_digit])

len(ovo_clf.estimators_)

训练一个RandomForestClassifier同样简单：

forest_clf.fit(X_train,y_train)
forest_clf.predict([some_digit])

这次 Scikit-Learn 没有必要去运行 OvO 或者 OvA，因为随机森林分类器能够直接将一个样例分到多个类别。可以调用predict_proba()，得到样例对应的类别的概率值的列表：

forest_clf.predict_proba([some_digit])

可以看到这个分类器相当确信它的预测：在数组的索引 5 上的 0.8，意味着这个模型以 80% 的概率估算这张图片代表数字 5。它也认为这个图片可能是数字 0 或者数字 3，分别都是 10% 的几率。

用cross_val_score()来评估SGDClassifier的精度。

cross_val_score(sgd_clf,X_train,y_train,cv = 3,scoring = "accuracy")

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))
cross_val_score(sgd_clf,X_train_scaled,y_train,cv = 3,scoring = "accuracy")

误差分析

假设已经找到一个不错的模型，找到方法去改善它。一个方式是分析模型产生的误差的类型。

首先，你可以检查混淆矩阵。你需要使用cross_val_predict()做出预测，然后调用confusion_matrix()函数，像你早前做的那样。

y_train_pred = cross_val_predict(sgd_clf,X_train_scaled,y_train,cv = 3)
conf_mx = confusion_matrix(y_train,y_train_pred)
conf_mx

这里是一对数字。使用 Matplotlib 的matshow()函数，将混淆矩阵以图像的方式呈现，将会更加方便。

fig = plt.figure(figsize = (8,8))
ax = fig.add_subplot(111)
cax =ax.matshow(conf_mx)
fig.colorbar(cax)

 

plt.matshow(conf_mx,cmap = plt.cm.gray)
save_fig("confusion_matrix_plot",tight_layout = False)
plt.show()

这个混淆矩阵看起来相当好，因为大多数的图片在主对角线上。在主对角线上意味着被分类正确。数字 5 对应的格子看起来比其他数字要暗淡许多。这可能是数据集当中数字 5 的图片比较少，又或者是分类器对于数字 5 的表现不如其他数字那么好。你可以验证两种情况。

让我们关注仅包含误差数据的图像呈现。首先你需要将混淆矩阵的每一个值除以相应类别的图片的总数目。这样子，你可以比较错误率，而不是绝对的错误数（这对大的类别不公平）。

row_sums = conf_mx.sum(axis = 1,keepdims = True)
norm_conf_mx = conf_mx / row_sums

用 0 来填充对角线。这样子就只保留了被错误分类的数据,画出这个结果。

np.fill_diagonal(norm_conf_mx,0)
fig = plt.figure(figsize = (8,8))
ax = fig.add_subplot(111)
cax =ax.matshow(norm_conf_mx)
fig.colorbar(cax)
saving_fig("confusion_matrix_errors_plot",tight_layout = False)
plt.show()

 

np.fill_diagonal(norm_conf_mx,0)
plt.matshow(norm_conf_mx,cmap = plt.cm.gray)
save_fig("confusion_matrix_errors_plot",tight_layout = False)
plt.show()

现在可以清楚看出分类器制造出来的各类误差。记住：行代表实际类别，列代表预测的类别。第 8、9 列相当亮，这告诉你许多图片被误分成数字 8 或者数字 9。相似的，第 8、9 行也相当亮，告诉你数字 8、数字 9 经常被误以为是其他数字。相反，一些行相当黑，比如第一行：这意味着大部分的数字 1 被正确分类（一些被误分类为数字 8 ）。留意到误差图不是严格对称的。举例子，比起将数字 8 误分类为数字 5 的数量，有更多的数字 5 被误分类为数字 8。

分析独特的误差，是获得关于分类器是如何工作及其为什么失败的一个好途径。但是这相对难和耗时。举例子，可以画出数字 3 和 5 的例子

cl_a,cl_b = 3,5
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]
plt.figure(figsize = (8,8))
plt.subplot(221);plot_digits(X_aa[:25],images_per_row = 5)
plt.subplot(222);plot_digits(X_ab[:25],images_per_row = 5)
plt.subplot(223);plot_digits(X_ba[:25],images_per_row = 5)
plt.subplot(224);plot_digits(X_bb[:25],images_per_row = 5)
save_fig("error_analysis_digit_plot")
plt.show()

左边两个5*5的块将数字识别为 3，右边的将数字识别为 5。一些被分类器错误分类的数字（比如左下角和右上角的块）是书写地相当差，甚至让人类分类都会觉得很困难（比如第 8 行第 1 列的数字 5，看起来非常像数字 3 ）。但是，大部分被误分类的数字，在我们看来都是显而易见的错误。很难明白为什么分类器会分错。原因是我们使用的简单的SGDClassifier，这是一个线性模型。它所做的全部工作就是分配一个类权重给每一个像素，然后当它看到一张新的图片，它就将加权的像素强度相加，每个类得到一个新的值。所以，因为 3 和 5 只有一小部分的像素有差异，这个模型很容易混淆它们。

3 和 5 之间的主要差异是连接顶部的线和底部的线的细线的位置。如果你画一个 3，连接处稍微向左偏移，分类器很可能将它分类成 5。反之亦然。换一个说法，这个分类器对于图片的位移和旋转相当敏感。所以，减轻 3/5 混淆的一个方法是对图片进行预处理，确保它们都很好地中心化和不过度旋转。这同样很可能帮助减轻其他类型的错误。

多标签分类

到目前为止，所有的样例都总是被分配到仅一个类。有些情况下，你也许想让你的分类器给一个样例输出多个类别。比如说，思考一个人脸识别器。如果对于同一张图片，它识别出几个人，它应该做什么？当然它应该给每一个它识别出的人贴上一个标签。比方说，这个分类器被训练成识别三个人脸，Alice，Bob，Charlie；然后当它被输入一张含有 Alice 和 Bob 的图片，它应该输出[1, 0, 1]（意思是：Alice 是，Bob 不是，Charlie 是）。这种输出多个二值标签的分类系统被叫做多标签分类系统。

目前我们不打算深入脸部识别。我们可以先看一个简单点的例子，仅仅是为了阐明的目的。

from sklearn.neighbors import KNeighborsClassifier
y_train_large = (y_train >= 7)
y_train_odd = (y_train % 2 == 1)
y_multilabel = np.c_[y_train_large,y_train_odd]
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train,y_multilabel)

这段代码创造了一个y_multilabel数组，里面包含两个目标标签。第一个标签指出这个数字是否为大数字（7，8 或者 9），第二个标签指出这个数字是否是奇数。接下来几行代码会创建一个KNeighborsClassifier样例（它支持多标签分类，但不是所有分类器都可以），然后使用多目标数组来训练它。现在可以生成一个预测，然后它输出两个标签：

knn_clf.predict([some_digit])

数字 5 不是大数（False），同时是一个奇数（True）。

有许多方法去评估一个多标签分类器，和选择正确的量度标准，这取决于你的项目。举个例子，一个方法是对每个个体标签去量度 F1 值（或者前面讨论过的其他任意的二分类器的量度标准），然后计算平均值。下面的代码计算全部标签的平均 F1 值：

警告:以下单元可能需要很长时间(可能需要几个小时，这取决于您的硬件)。

y_train_knn_pred = cross_val_predict(knn_clf,X_train,y_multilabel,cv = 3,n_jobs = 1)

f1_score(y_multilabel,y_train_knn_pred,average = "macro")

这里假设所有标签有着同等的重要性，但可能不是这样。特别是，如果你的 Alice 的照片比 Bob 或者 Charlie 更多的时候，也许你想让分类器在 Alice 的照片上具有更大的权重。一个简单的选项是：给每一个标签的权重等于它的支持度（比如，那个标签的样例的数目）。为了做到这点，简单地在上面代码中设置average="weighted"。

多输出分类

即将讨论”多输出-多类分类”（或者简称为多输出分类）。它是多标签分类的简单泛化，在这里每一个标签可以是多类别的（比如说，它可以有多于两个可能值）。

为了说明这点，建立一个系统，可以去除图片当中的噪音。它将一张混有噪音的图片作为输入，期待它输出一张干净的数字图片，用一个像素强度的数组表示，就像 MNIST 图片那样。注意到这个分类器的输出是多标签的（一个像素一个标签）和每个标签可以有多个值（像素强度取值范围从 0 到 255）。所以它是一个多输出分类系统的例子。

分类与回归之间的界限是模糊的，比如这个例子。按理说，预测一个像素的强度更类似于一个回归任务，而不是一个分类任务。而且，多输出系统不限于分类任务。你甚至可以让你一个系统给每一个样例都输出多个标签，包括类标签和值标签。

从 MNIST 的图片创建训练集和测试集开始，然后给图片的像素强度添加噪声，这里是用 NumPy 的randint()函数。目标图像是原始图像。

noise = np.random.randint(0,100,(len(X_train),784))
X_train_mod = X_train + noise
noise = np.random.randint(0,100,(len(X_test),784))
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test

看一下测试集当中的一张图片：

some_index = 5500
plt.subplot(121);plot_digit(X_test_mod[some_index])
plt.subplot(122);plot_digit(y_test_mod[some_index])
save_fig("noisy_digit_example_plot")
plt.show()

 

左边的加噪声的输入图片。右边是干净的目标图片。现在训练分类器，让它清洁这张图片：

knn_clf.fit(X_train_mod,y_train_mod)
clean_digit = knn.clf.predict([X_test_mod[some_index]])
plot_digit(clean_digit)
save_fig("clean_digit_example_plot")

 

看起来足够接近目标图片。现在总结我们的分类之旅。希望你现在应该知道如何选择好的量度标准，挑选出合适的准确率/召回率的折衷方案，比较分类器，更概括地说，就是为不同的任务建立起好的分类系统。

额外分类器

（1）Dummy（随机）分类器

from sklearn.dummy import DummyClassifier
dmy_clf = DummyClassifier()
y_probas_dmy = cross_val_predict(dmy_clf,X_train,y_train_5,cv = 3,method = "predict_proba")
y_scores_dmy = y_probas_dmy[:,1]
fprr,tprr,thresholdsr = roc_curve(y_train_5,y_scores_dmy)
plot_roc_curve(fprr,tprr)

（2）KNN分类器

from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier(n_jobs = -1,weights = 'distance',n_neighbors = 4)
knn_clf.fit(X_train,y_train)

y_knn_pred = knn_clf.predict(X_test)
from sklearn.metrics import accuracy_score
accuracy_score(y_test,y_knn_pred)

from scipy.ndimage.interpolation import shift
def shift_digit(digit_array,dx,dy,new = 0):
    return shift(digit_array.reshape(28,28),[dx,dy].cval = new).reshape(784)
plot_digit(shift_digit(some_digit,5,1,new = 100))

一个简单的数据偏移完成，接下来对整个训练集进行扩充

X_train_expanded = [X_train]
y_train_expanded = [y_train]
for dx,dy in ((1,0),(-1,0),(0,1),(0,-1)):
    shifted_images = np.apply_along_axis(shift_digit,axis = 1,arr = X_train,dx= dx,dy = dy)
    X_train_expanded.append(shifted_images)
    y_train_expanded.append(y_train)
X_train_expanded = np.concatenate(X_train_expanded)
y_train_expanded = np.concatenate(y_train_expanded)
X_train_expanded.shape, y_train_expanded.shape    

数据增加大了30万之多，有了更多的数据，接下来进行训练、预测，计算精度

knn_clf.fit(X_train_expanded,y_train_expanded) 

y_knn_expanded_pred = knn_clf.predict(X_test) 
accuracy_score(y_test,y_knn_expanded_pred)

 

ambiguous_digit = X_test[2589]
knn_clf.predict_proba([ambiguous_digit])

plot_digit(ambiguous_digit)

习题答案

1.MNIST分类准确率达97%以上

尝试在 MNIST 数据集上建立一个分类器，使它在测试集上的精度超过 97%。提示：KNeighborsClassifier非常适合这个任务。只需要找出一个好的超参数值（试一下对权重和超参数n_neighbors进行网格搜索）。

from sklearn.model_selection import GridSearchCV
params_grid = [{'weights': ["uniform","diatance"],
                'n_neighbors': [3,4,5]}]
knn_clf = KNeighborsClassifier()
grid_search = GridSearchCV(knn_clf,params_grid,cv = 5,verbose = 3,n_jobs = 1)
grid_search.fit(X_train,y_train)

grid_search.best_params_

grid_search.best_score_

from sklearn.metrics import accuracy_score
y_pred = grid_search.predict(X_test)
accuracy_score(y_test,y_pred)

2.数据增强

另一种表达方式：

 

from scipy.ndimage.interpolation import shift
def shift_image(image,dx,dy):
    image = image.reshape(28,28)
    shifted_image = shift(image,[dy,dx],cval = 0,mode = "constant")
    return shifted_image.reshape([-1])
image = X_train[1000]
shifted_image_down = shift_image(image,0,5)
shifted_image_left = shift_image(image,-5,0)

plt.figure(figsize = (12,3))
plt.subplot(131)
plt.title("Original",fontsize = 14)
plt.imshow(image.reshape(28,28),interpolation = "nearest",cmap = "Greys")
plt.subplot(132)
plt.title("Shifted down",fontsize = 14)
plt.imshow(shifted_image_down.reshape(28,28),interpolation = "nearest",cmap = "Greys")
plt.subplot(133)
plt.title("Shifted left",fontsize = 14)
plt.imshow(shifted_image_left.reshape(28,28),interpolation = "nearest",cmap = "Greys")
plt.show()

 

X_train_augmented = [image for inage in X_train]
y_train_augmented = [label for label in y_train]
for dx,dy in ((1,0),(-1,0),(0,1),(0,-1)):
    for image,label in zip(X_train,y_train):    
        X_train_augmented.append(shifted_image(image,dx,dy))
        y_train_augmented.append(label)
X_train_augmented = np.array(X_train_augmented)
y_train_augmented = np.array(y_train_augmented)

shuffle_idx = np.random.permutation(len(X_train_augmented))
X_train_augmented = X_train_augmented[shuffle_idx]
y_train_augmented = y_train_augmented[shuffle_idx]

knn_clf = KNeighborsClassifier(**grid_search.best_params_)
knn_clf.fit(X_train_augmented,y_train_augmented)

y_pred = knn_clf.predict(X_test)
accuracy_score(y_test,y_pred)

 

此时准确率已达到97%以上。