深度学习——神经网络之DNN全连接神经网络、BP算法原理

深度学习——神经网络之DNN全连接神经网络、BP算法原理

1、啥是人工神经网络

神经网路模型是深度学习中一个非常经典的模型，后面的卷积神经网络CNN，递推神经网络RNN都是围绕神经网络展开的，先看一下神经网络经典的定义：

Kohonen说：“神经网络是由具有适应性的简单单元组成的广泛并行互连网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应”

懵逼不，是不是听起来很高大上，我开始也想不明白两者有毛关系。

---

2、神经网络的应用

神经网络类型的算法在AI中运用的是非常广泛的，比如：

• 语音识别，声纹识别
• 图像应用

大规模(大数据量)图片识别(聚类/分类)
基于图片的搜索服务
目标检测

• NLP(自然语言)，知识图谱(基于知识图谱的问答什么的)
• 游戏、机器人、推荐系统等
• 数据挖掘(聚类、分类、回归等问题)

---

3、神经网络的组成

3.1、神经元

  先来看一张图：

  上面就是一个神经元，这个神经元对应x1,x2,x3,+1,三个输入，一个输出

输入：x1,x2,x3,和截距 +1
输出：函数 h_w,b(x),其中w,b是参数

  神经元对三个输入做了一个线性变化，若果只有普通的线性变换，就是一个普通的感知器（感知器的内容会在机器学习部分单独介绍）。
  神经元对传入数据做简单的线性组合之后还会进过一个激活函数输出。

  就是说，神经元接收传入的信号（开始输入的，或者上一层神经元输出的），每个输入都带有一个权重W，神经元把这些信号加在一起，得到一个总的输入值，将总的输入值与神经元的阈值b进行对比，然后在通过一个激活函数，处理得到最终的输出，这个输出再作为下一层神经元的输入，迭代这个步骤，得到最后的输出。
  其实一个神经元做的就是一个分类的任务，每一个神经元加上激活函数，映射到一个更高维的空间中

3.2、激活函数

  上边的 f 被称为激活函数，常用激活函数

• tanh（逻辑回归函数）
  绿色图像
  值域：(-1,1)
  
  

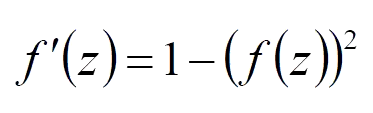
• sigmoid（双曲正切函数）
  红色图像
  值域：(0,1)
  
  

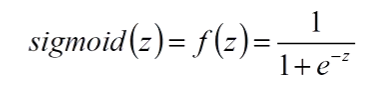
• relu函数
  值域：[0,+∞]
  

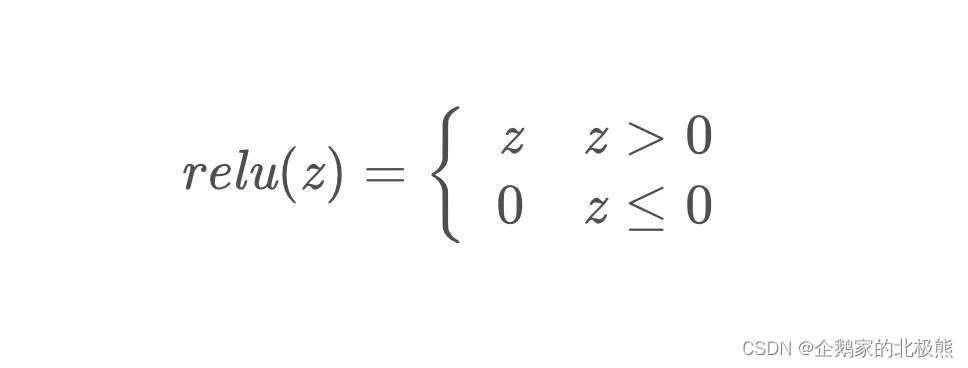
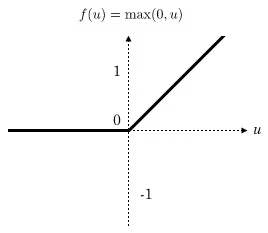
  加一个激活函数的目的是，如果我们不加激活函数，无论经过多少层的神经元处理，最后的到的都是一个线性的映射，然而现实的问题是很复杂的，不具有线性相关，那么这个时候单纯的线性银蛇就不能解决线性不可分的问题（非线性问题），经过激活函数，做非线性映射，就可以解决更复杂的非线性问题。

---

3、神经网络之感知器

  当激活函数的返回值是两个固定值的时候，可以称为此时的神经网络为感知器

  因为感知器的返回值只有两种情况，所以感知器只能解决二类线性可分的问题，感知器比较适合应用到模式分类问题中

---

4、神经网络之线性神经网络

  线性神经网络是一种简单的神经网络，可以包含多个神经元;激活函数是一个线性函数，可以返回多个值，常用的激活函数为sigmoid函数和tanh函数
  线性神经网络和感知器一样，只适合线性可分类问题;但是效果比感知器要好，而且可以做多分类问题

---

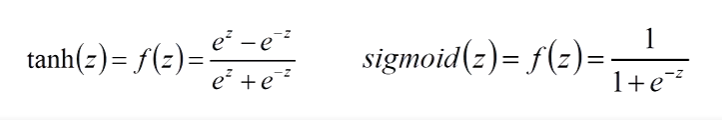
5、神经网络之深度神经网络

  增多中间层(隐层)的神经网络就叫做深度神经网络(DNN);可以认为深度学习是神经网络的一个发展，除了输入层，输出层，剩下的就都是隐含层了。

  当层数超过3层时，就可以说是一个深度神经网络，在神经网络中的传递方向，可以看做是一个前馈传递，比如上图中的输出层的每一个输入，全部链接到第二次层的一个神经元，然后加上一个激活函数，作为下一层神经元的输出。每个神经元前馈传递到下一层的参数W也就是权重都是不一样的。看一下下边这张图，更加清晰：

解释：
  输入层的每一个x作为第一个隐含层第一个神经元的输入，输入的时候每一个x*w求和做一个线性变换，加上一个偏置项b，在通过激活函数，作为第二层隐含层第一个神经元的输入。第一层的隐含层的每一个神经圆的输出最为他的输入，但是这个时候w就不再是原来的了，或者说每一个神经元，记住是每一个神经元都有一组w，我们的目标就是通过训练，不断地更新每一个神经元的w，使得模型预测达到最好的效果。

  假设，我们对一个77的图片进行识别，那么这个时候，如果用全连接网络进行预测，那就把每一张图片的像素点作为一个特征x，将所有的像素点拉平，就是49的输入，如果我们第二层依然有49个神经元，那么输入层与第一个隐含层之间就应该有4949个w。
  至于有多少个隐含层，每个隐含层有多少的神经元，那就是你自己设计的事情了。

---

6、神经网络直观理解之非线性可分

  看下边这个例子：

这里的 w_ji 是一种通用的表示方法

j 表：示当前神经元所在编号
i 表：示上一层对应的神经元的编号

  这里的W_j表示上一层和当前神经元 j 连接的所有w，比如：
w₂ = [w₂₀，w₂₁，w₂₂]
  现在计算 z₁的输出结果：

然后经过激活函数，最后结果为0。

  然后我们要进行预测吗，所以我们要设计一个目标值y，计算得到的h(x)与真实值进行比较，计算误差（均方函数等）迭代更新W。使得h(x)更接近真实值。

---

7、神经网络之BP算法

  上面我们计算出了预测值与真实值的误差，我们的目的是得到一组使得模型预测效果好的参数w，我们肯定是希望这个误差越小越好，通过一些算法，迭代更新w，使得下一次训练的效果更好。这个反向更新w的算法就是BP算法。
  实质上是通过误差，进行反向传播，一直到输入层，将误差分摊给各个层的神经元，进行更新，这个地方有必要看一下机器学习中极大似然函数和梯度下降算法，我也说不太清楚，借着往下看吧，总之就记住是通过损失函数来更新w一层一层的更新，相当于每一个神经元的传播都是机器学习中的线性回归求解最优参数的问题。嗯，就这么理解吧。

  输出层误差：

  隐含层误差

  输入层误差：

  公式不明白是吧，没事，就是对上面叙述内容转换成数学公式是矩阵的计算你只要明白算法的原理就行，矩阵计算可以试一试嘛查一查。。

  误差E有了，那么为了使误差越来越小，可以采用随机梯度下降的方式进行w和v的求解，即求得w和v使得误差E最小

  梯度下降算法自行补吧，在机器学习模块

---

8、BP算法例子

8.1 前馈传播过程

  以这个例子为例;

这里我们定义:
net表示：只进行了线性变换，没有进行激活函数
out表示：经过激活函数的输出结果
小下标表示：对应的神经元
w表示权值
b表示偏置项

1、第一层（隐含层）的计算：

• 计算每一个神经元的线性变换结果net，这里以h₁为例：

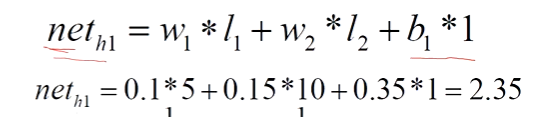
• 将每一个神经元线性变换后的结果带入激活函数得出每一个神经元对应的out，依然以h₁为例
  这里激活函数我们用sigmoid函数
  
  同理计算两外两个得到：
  

2、第二层（输出层）的计算
第二层的输入结果是第一层的out

• 经过激活函数之前net
  
  
• 经过激活函数之后out

3、计算误差
计算误差，这里我们采用均方差
真实值我们定义为：0.01和0.09

8.2、反向传播

知道了误差就要进行反向传播来更新w
我们以o₁的反向传播为例;

我们要更新的就是W7，W9，W11，b2，我们首先来更新W7，就是对W7求偏导数，这个时候可以看成符合函数的求导过程，高数的知识自己撸吧。

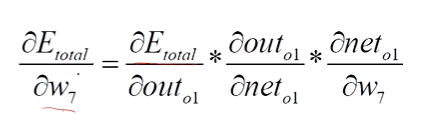
1、E对out₀₁求偏导数

2、out₀₁对net_o1求偏导数

sigmoid求导公式：

3、net对w7求偏导数


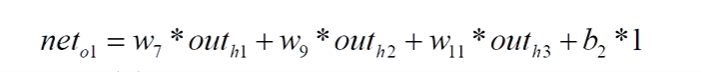
最终：

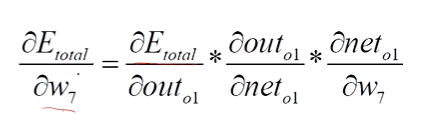
  同理我们计算其他的w偏导数
这是求的w1偏导数：

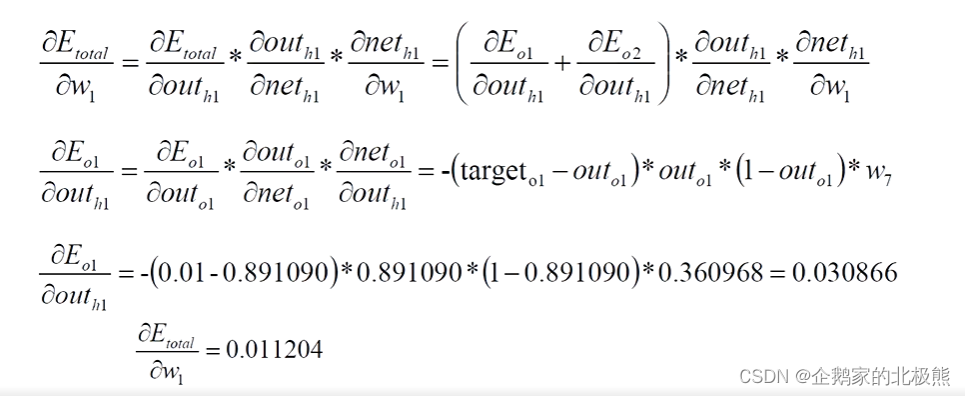
  这里你要注意，W1对两个输出都有关，所以有这步这块不明白查看一下高数部分积和差倒数计算规则：

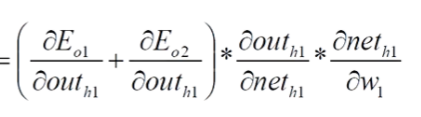
8.3、梯度更新

  梯度更新公式就是梯度下降算法的梯度更新：
原值-学习率（步长）* 梯度，这里我们以w1为例：

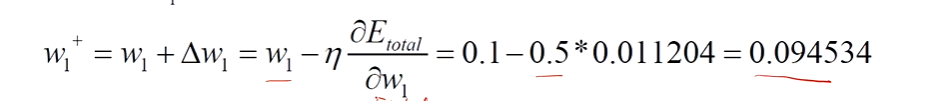
这里的学习率可以固定，也可以随着训练的过程衰减。
经过一轮的更新：

  全部的参数都更新以后，是一次的更新，得到新的W，再进行新数据的训练。
  上面我们只有一个样本，一个样本经过模型的时候我们更新一次W，但是我们不可能只有一个样本，也就是说，所有样本都进来一次算是一次训练但是我们如果每个样本进来都更新一次，像上面一样，那速度可就太慢了，怎么处理？

这里我们就采用随机梯度下降
就是每一次对小批次样本进行训练，然后随机更新一次W

9、BP算法的代码实现

# 课程内容：BP算法例子（不包含截距项）
# 开发时间： 14:37
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
class BPNet:

    def __init__(self,inputnum,hid1num,outputnum,epoch):
        self.w_lay1 = np.random.random((inputnum,hid1num))#第一层权值矩阵
        self.w_lay2 = np.random.random((hid1num,outputnum))#第二层权值矩阵
        self.lr = 0.1#学习率
        self.epoch = epoch#迭代次数
    #前馈计算
    def forward(self,x):
        """
        上一层的输出作为下一层的输入
        """
        #对输入进行线性变换
        neth = np.dot(x,self.w_lay1)
        # sigmoid激活
        self.outh = self.sigmoid(neth)
        #下一层线性变换
        neto = np.dot(self.outh,self.w_lay2)
        #激活
        self.outo = self.sigmoid(neto)
    #计算误差
    def loss(self,y):
        return (sum(self.outo - y)**2)/2

    #反向传播
    def backward(self,x,y):
        self.w_lay2_d = np.dot(self.outh.T,(self.outo - y) * self.outo * (1 - self.outo))
        self.w_lay1_d = np.dot(x.T,(self.outo-y) * self.outo * (1 - self.outo) * self.w_lay2.T * self.outh * (1 - self.outh))

    #更新梯度（权值）
    def cal_gred(self):
        self.w_lay1 -= self.lr * self.w_lay1_d
        self.w_lay2 -= self.lr * self.w_lay2_d
    #训练
    def train(self,x,y):
        count = 1
        error = []
        while count  <= self.epoch:
            #前向计算
            self.forward(x)
            error.append(self.loss(y))
            #反向传播
            self.backward(x,y)
            #梯度更新
            self.cal_gred()
            count += 1
        self.draw_loss(error)
    #测试
    def predict(self,x):
        #前向计算
        y_hat = self.forward(x)
        return y_hat

    #绘制损失线性图
    def draw_loss(self,error):
        x_ = range(0,self.epoch)
        plt.plot(x_,error)
        plt.show()
    #sigmoid激活函数(静态方法方法)
    @staticmethod
    def sigmoid(z):
        #公式：1/(1+exp(-z))
        return 1/(1+np.exp(-z))



if __name__ == '__main__':
    np.random.seed(200)
    data = pd.read_excel('BPnet_data.xlsx')
    train_x = np.array(data.iloc[:,:-1])
    train_y = np.array(data.iloc[:,-1:])
    bpnet = BPNet(3,4,1,20)
    bpnet.train(train_x,train_y)
    print(bpnet.predict(train_x))

输出：
可以看到，效果还是很好的，只有一层隐含层的强狂下，到了第5次左右训练迭代，错误率就几乎为0了。

如果梯度下降不明白，在机器学习模块有相关的讲解，数学的知识就自己补充吧，有一本书叫《程序员的数学》够用。