各种遍历序列确定二叉树分析与总结

遍历序列确定二叉树：
一个遍历序列不可能确定唯一的一个二叉树。

先序和中序遍历序列，确定二叉树

已知同一个二叉树的先序和中序遍历序列，能确定吗？
主要看中序遍历序列划分左右子树，一直分下去。
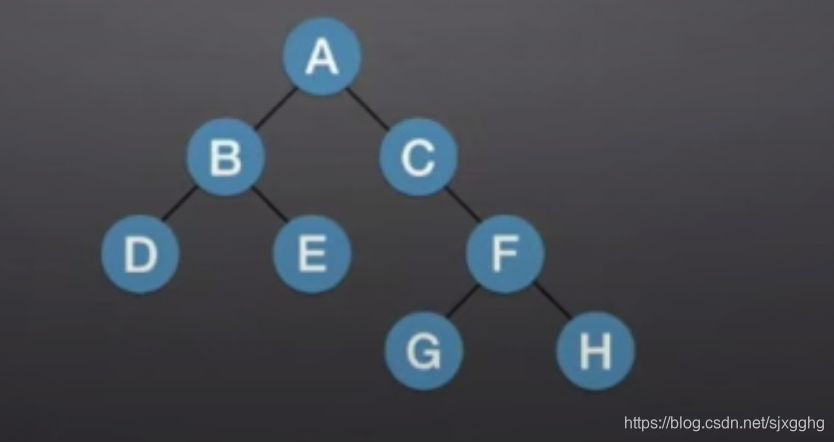
先序：ABDECFGH（根左右）
中序：DBEACGFH（左根右）

先序看到A，A在中序的中间，所以A既有左子树又有右子树。
A的左子树为DBE，A的右子树为CGFH

对DBE分析：
先序BDE，中序DBE，
先序看到B，B在中序中间，所有B既有左子树又有右子树。
所以B的左孩子是D,B的右孩子是E。

对CGFH分析：
先序CFGH，后序CGFH
先序看到C，中序看到C在最左边，所以C没有左孩子。

根左 右 -> 根右
左 根右 -> 根右
这种判断方式是我个人这么在干，
根不能删掉，当我们删掉左了之后，发现先序和后序都是根右结构，推出没有左孩子

若先序为 CFGH，后序为GHFC
根左右 -> 根左
左根右 ->左根
我们把FGH看成一个整体，发现我们删掉右，发现前序是根左，后序是左根符合题意，推出没有右孩子。

…

代码：
这的i是我们通过for循环来得到的下标i的值
确定左边一半：

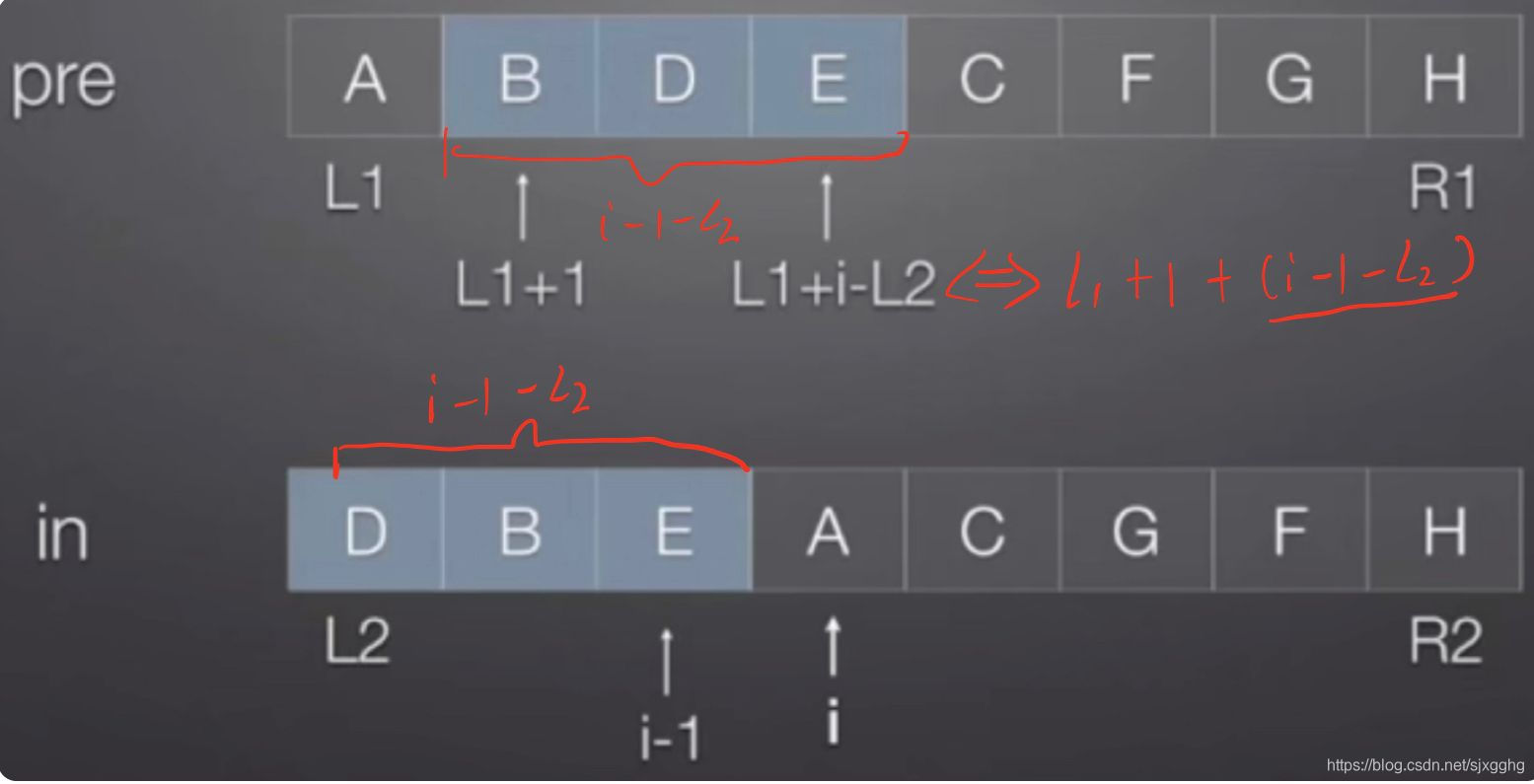
确定右边一半：

BTNode *CreatBT(char pre[],char in[],int L1,int R1,int L2,int R2)
{
    //pre[]元素的下标范围为L1~R1
    // in[]元素的下标范围为L2~R2
    if(L1 > R1)
        return NULL;
    BTNode *s = (BTNode *)malloc(sizeof(BTNode));
    s->lChild = s->rChild = NULL;
    s->data = pre[L1];

    int i;
    //此时中序遍历序列被划分成了2部分
    for(int i = L2;i < R2; ++i)
        if(in[i] == pre[L1])
            break;
    s->lChild = CreatBT(pre,in,L1+1,L1+i-L2,L2,i-1);
    s->rChild = CreatBT(pre,in,L1+i-L2+1,R1,i+1,R2);
    return s;
}

后序和中序遍历序列，确定二叉树

思路分析：
1.后序序列的最后一个是根（这个是突破口）
2.然后再根据中序序列划分左右子树
这个序列的难点是：
后序：GHFC
中序：CGFH
用我们前面提到的方法：
（根不删）
左 右根
左 根右
我们发现把左删除后，恰好是上面的结构，推出C没有右孩子。

BTNode *CreatBT(char post[],char in[],int L1,int R1,int L2,int R2)
{
    //pre[]元素的下标范围为L1~R1
    // in[]元素的下标范围为L2~R2
    if(L1 > R1)
        return NULL;
    BTNode *s = (BTNode *)malloc(sizeof(BTNode));
    s->lChild = s->rChild = NULL;
    s->data = post[R1];

    int i;
    //此时中序遍历序列被划分成了2部分
    for(int i = L2;i < R2; ++i)
        if(in[i] == post[R2])//R2,最后一个
            break;
    s->lChild = CreatBT(post,in,L1,L1+i-L2-1,L2,i-1);
    s->rChild = CreatBT(pre,in,L1+i-L2,R1,i+1,R2);
    return s;
}

层次遍历序列和中序遍历序列，确定二叉树

（不是正规解法，只是我这么在写）
中序：左根右
 层次看到A，A是二叉树的根。看到A在中序的中间，DBE,CGFH分别是A的左右子树。
 然后根据层次遍历推出，既然A有左右子树，那么B一定是A的左孩子，C一定是A的右孩子。
层次：ABC DE FGH
中序：DBEACGFH
由于B在DE中间，把DE再划掉。
我们分析C的左边是A，（中序遍历结构是左根右）我们发现A的左边是A的父结点，推出A没有左孩子。
层次还剩下FGH，把C看作根结点，由于GFH在中序遍历C的右边，所以GFH全部属于C的子树。
然后就剩下3个结点，可以轻松推出来了。

int search(char arr[],char key,int L,int R)
{
    //key待查找的关键字
    int idx;
    for(idx = L;idx <= R; ++idx)
    {
        if(arr[idx] == key)
            return idx;
    }
    return -1;
}

void getSubLevel(char subLevel[],char level[],char in[],int n,int L,int R)
{
    //从level中获取子序列
    //n代表level的长度;L,R是in[]中当前需要取得元素范围
    int k = 0;
    for(int i=0;i<n;++i)
        //拿level[i]到in[]里面查找，找到了就插入subLevel[]中
        if(search(in,level[i],L,R) != -1)
            subLevel[k++] = level[i];
}

//在level处理的数据范围不是连续的
BTNode *CreateBT3(char level[],char in[],int n,int L,int R)
{
    if(L>R)
        return NULL;
    BTNode *s = (BTNode *)malloc(sizeof(BTNode));
    s->lChild = s->rChild = NULL;
    s->data = level[0];

    int i = search(in,level[0],L,R);
    int LN = i-L;char LLevel[LN];
    int RN = R-i;char RLevel[RN];
    getSubLevel(LLevel,level,in,n,L,i-1);
    getSubLevel(RLevel,level,in ,n,i+1,R);
    s->lChild = CreateBT3(LLevel,in,LN,L,i-1);
    s->rChild = CreateBT3(RLevel,in,RN,i+1,R);
}

先序和后序遍历，不能确定二叉树

先序：根左右
后序：左右根
只能确定根，不能确定左右子树。