最近各学科上都要用到微分方程的知识,发现自己微分方程差不多忘光了,而且由于书没有带回家,所以就想写个博客留着自己复习用。
先说一阶常微分方程:
有以下几种:
1.可分离变量型微分方程;
2.一阶齐次线性微分方程;
3.一阶非齐次线性微分方程;
4.伯努利方程;
他们彼此之间的联系是比较明显的,且看我对他们解法的总结。
可分离变量型微分方程:
一阶齐次线性微分方程(本质上是可分离变量的微分方程)
一阶非齐次线性微分方程
这里需要用到所谓的常数变易法:即是把一阶非齐次线性微分方程右边不为0的项变为0,这样就可以按一阶齐次线性微分方程解得此时的y,再把y的表达式中的任意常数变为关于x的方程(c(x)),再将此时y的表达式代回微分方程,反求出关于x的方程(c(x));
伯努利方程
接下来是高阶微分方程:
其实也就是可降阶微分方程和二阶微分方程;
可降阶微分方程:
二阶微分方程分为:
二阶常系数齐次线性微分方程;
二阶常系数非齐次线性微分方程;
关于证明可以看看b站上的这篇:二阶常系数齐次线性微分方程通解 - 哔哩哔哩 (bilibili.com)
https://www.bilibili.com/read/cv2769623讲的挺清楚的,而且有很惊喜的比喻。

那么,关于微分方程的通解就到此告一段落了。
第一次写博客,希望自己能坚持下去,我觉得写博客是一种很好的学习方式,写一篇博客没有想象中那么容易的。







 这篇博客主要回顾了一阶常微分方程的四种类型:可分离变量、齐次线性、非齐次线性和伯努利方程,以及高阶微分方程中的可降阶和二阶线性微分方程。通过常数变易法解决非齐次线性方程,并推荐了一个讲解二阶齐次线性微分方程的视频资源。作者认为写博客是有效的学习方式。
这篇博客主要回顾了一阶常微分方程的四种类型:可分离变量、齐次线性、非齐次线性和伯努利方程,以及高阶微分方程中的可降阶和二阶线性微分方程。通过常数变易法解决非齐次线性方程,并推荐了一个讲解二阶齐次线性微分方程的视频资源。作者认为写博客是有效的学习方式。






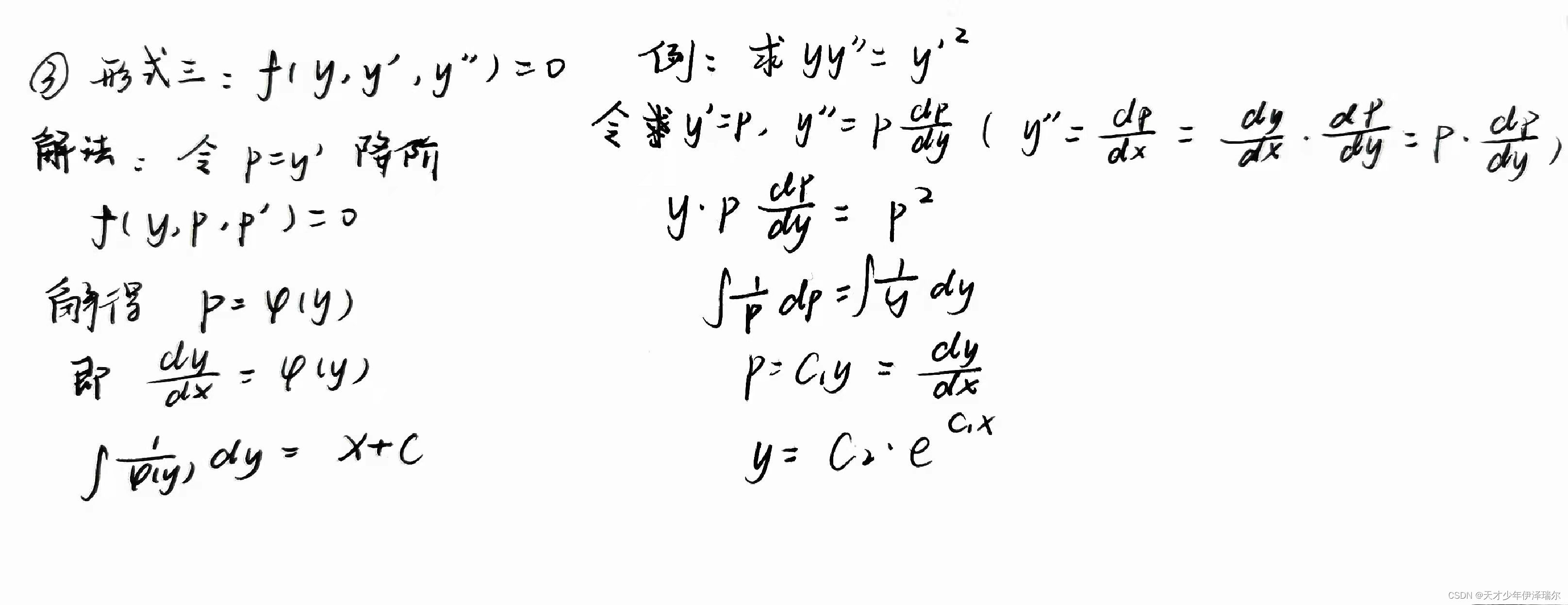


















 308
308

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








