找出数组中每个数右边第一个比它大的元素--时间复杂度o(n)单调栈解法

题目：给定一个整型数组，数组元素随机无序的，要求打印出所有元素右边第一个大于该元素的值。

如数组A=[1,5,3,6,4,8,9,10] 输出[5, 6, 6, 8, 8, 9, 10, -1]

如数组A=[8, 2, 5, 4, 3, 9, 7, 2, 5] 输出[9, 5, 9, 9, 9, -1, -1, 5, -1]

1、暴力遍历

我们很容易想到复杂度为O(n^2)的解法，遍历数组中的每一个后面所有元素，找到第一个大于它的，输出即可。代码实现如下：

public int[] findMaxRight(int[] array) { 
        if(array == null) {
            return array;
        }
        int size = array.length;
        int[] result = new int[size];
        for(int i = 0; i < size-1; i++) {
            for(int j = i+1; j < size; j++) {
                if(array[j] > array[i]) {
                    result[i] = array[j];
                    break;
                }
            }
        }
        result[size-1] = -1;//最后一个元素右边没有元素，所以肯定为-1
        return result;
    }

2、借助栈，时间复杂度O(n)

如果要求时间复杂度为O(n)呢，能不能遍历一次数组中元素，就可以找到右边第一个大于它的元素呢，当然是可行的，不过要借助数据结构栈。

具体思路是：我们用栈来保存未找到右边第一个比它大的元素的索引（保存索引是因为后面需要靠索引来给新数组赋值），初始时，栈里放的是第一个元素的索引0值。

步骤如下：

（1）初始化栈，里面为第一个元素索引0值；

（2）遍历到下一个元素A[i]

1) 如果栈不为空且当前遍历的元素值A[i]大于栈顶的元素值A[stack.peek()]，说明当前元素正好是栈顶元素右边第一个比它大的元素，将栈顶元素弹出，result[stack.pop()]=A[i]

继续遍历的元素值A[i]是否大于新栈顶元素值A[stack.peek()]，如果大于，说明A[i]也是比A[stack.peek()]右边第一个比它大的元素，将栈顶元素弹出，result[stack.pop()]=A[i]，一直循环，直到不满足条件1），即栈顶为空或是当前遍历的元素值小于栈顶元素索引处的值。

2) 如果栈为空，说明前面的元素都找到了比它右边大的元素，则直接将当前元素的索引放入栈中；

3）如果当前遍历的元素值A[i]小于栈顶元素索引的值A[stack.peek()]，说明还未找到栈顶元素中右边第一个比它大的元素，直接将当前遍历的元素的索引入栈即可stack.push(i);

将i++，重复步骤（2）

（3）直到遍历完所有元素，如果栈不为空，说明栈中保存的全是未找到右边第一个比它大的数组索引，我们依次将这些栈元素出栈，并赋值result[stack.pop()]=-1即可。

以A=[8, 2, 5, 4, 3, 9, 7, 2, 5] 举例

1) 初始栈顶元素数组的第一个索引0，栈顶A[stack.peek()]=A[0]=8

2) 遍历到下一个元素值为2，它比栈顶A[stack.peek()]=A[0]=8元素值小，即上面第(2)步中的第3）种情况，直接将该元素的索引入栈，栈中元素是1, 0, 栈顶A[stack.peek()]=A[1]=2

3) 遍历到下一个元素值为5，它比栈顶A[stack.peek()]=A[1]=2元素值大，即上面第(2)步中的第1）种情况，将栈顶元素出栈，并且赋值result[stack.pop()]=result[1]=5，现在栈中还剩下 0, 栈顶A[stack.peek()]=A[0]=8

接着判断当前遍历的元素值5是否在大于栈顶A[stack.peek()]=A[0]=8，发现小于栈顶元素，即上面第(2)步中的第3）种情况，直接将该元素的索引入栈，栈中元素是2, 0, 栈顶A[stack.peek()]=A[2]=5

4) 遍历到下一个元素值为4，它比栈顶A[stack.peek()]=A[2]=5元素值小，直接将该元素的索引入栈，栈中元素是3，2, 0, 栈顶A[stack.peek()]=A[3]=4

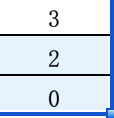
5) 遍历到下一个元素值为3，它比栈顶A[stack.peek()]=A[3]=4元素值小，直接将该元素的索引入栈，栈中元素是4，3，2, 0, 栈顶A[stack.peek()]=A[4]=3

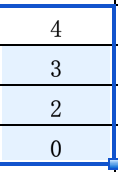
6) 遍历到下一个元素值为9，它比栈顶A[stack.peek()]=A[4]=3元素值大，将栈顶元素出栈，并且赋值result[stack.pop()]=result[4]=9，现在栈中还剩下3, 2, 0, ....重复这个步骤，最终都因为9比栈顶元素大，栈中元素出栈，最终result[3]=9, result[2]=9, result[0]=9， 直到栈中元素都出栈了，栈为空，变成上面的(2) 3) 情况，直接将当前元素索引值存入栈。即栈顶A[stack.peek()]=A[5]=9

7) 遍历到下一个元素值为7，它比栈顶A[stack.peek()]=A[5]=9元素值小，直接将该元素的索引入栈，栈中元素是6,5, 栈顶A[stack.peek()]=A[6]=7

8) 遍历到下一个元素值为2，它比栈顶A[stack.peek()]=A[6]=7元素值小，直接将该元素的索引入栈，栈中元素是7, 6,5, 栈顶A[stack.peek()]=A[7]=2

9) 遍历到下一个元素值为5，它比栈顶A[stack.peek()]=A[7]=2元素值大，将栈顶元素出栈，并且赋值result[stack.pop()]=result[7]=5，现在栈中还剩下6, 5， 栈顶元素A[stack.peek()]=A[6]=7比当前处理的元素值5大，所以将当前元素的索引值入栈，栈中变成8, 6, 5

由于元素遍历完了，栈中还保存的元素代表该索引处找不到右边第一个比它大的元素值了，所以挨个将栈中元素出栈，并赋值result[8]=-1, result[6]=-1, result[5]=-1

输出[9, 5, 9, 9, 9, -1, -1, 5, -1]

可以看到只需要遍历一次，就把数组中每个右边比它大的元素输出了。

具体代码实现如下：

public int[] findMaxRightWithStack(int[] array) {
        if(array == null) {
            return array;
        }
        int size = array.length;
        int[] result = new int[size];
        Stack<Integer> stack = new Stack<>();
        stack.push(0);
        int index = 1;
        while(index < size) {
            if(!stack.isEmpty() && array[index] > array[stack.peek()]) {
                result[stack.pop()] = array[index];
            } else {
                stack.push(index);
                index++;
            }
        }
        if(!stack.isEmpty()) {
            result[stack.pop()] = -1;
        }
        return result;
    }

总结：

第二种方是以空间换时间，用到了数据结构栈，用到了单调栈思想，单调栈可以用来解决一类问题，单调栈是指：栈内元素保持一定单调性（单调递增或单调递减）的栈。这里的单调递增或递减是指的从栈顶到栈底单调递增或递减。既然是栈，就满足后进先出的特点。与之相对应的是单调队列。

具体可参考这篇文章：单调栈原理及应用 详解 附各种类型的题目练习

利用单调栈解决此问题，尤其在数据量特别大的时候，第二种方法带来的时间上的优势会非常明显。