面试题------全排列的非递归和递归实现(含重复元素)

  全排列算法难度适中，既可以递归实现，又能用非递归的实现，可以考察解决问题的基本能力。在校园招聘的笔试和面试中经常出现。

1.排列问题描述

  有$n$个元素，分别编号为$1、2、3...、n$。排列问题就是要生成这$n$个元素的全排列。假定这$n$个元素已按编号次序由小到大存放着数组$A$中，可以认为数组中存放的就是元素的编号。

例如，123的全排列有123、132、213、231、312、321这六种。
例如，abc 的全排列有abc、acb、bca、dac、 cab、cba这六种。

2.算法的分析 和 设计

  只有找到生成元素全排列的规律，才能找到递归关系。分析递归关系，找到递归出口和递归关系式，最终才能设计出递归的函数实现。
递归算法设计如下：
【1】将规模为$n$的全排列问题转化为规模为$n-1$的全排列问题。

基本思想就是：任意选一个数（一般从小到大或者从左到右）打头，对后面的n-1个数进行全排列。

例如：（A、B、C、D）的全排列为

• A后面跟（B、C、D）的全排列
• B后面跟（A、C、D）的全排列
• C后面跟（A、B、D）的全排列
• D后面跟（A、B、C）的全排列

【2】将规模为$n-1$的全排列问题转化为规模为$n-2$的全排列问题。实现方法类似【1】。
【3】将规模为$n-2$的全排列问题转化为规模为$n-3$的全排列问题。实现方法类似【1】。

  以此类推….
  最终，问题的规模一级一级降至$1,1$个元素的全排列就是它本身，这也就是递归出口。

3.递归算法描述和C实现

  假定全排列算法为：void permutation(char *A,int k,int n)。生成数组$A[n]$后面$k$个元素的全排列。

  当$k==1$时，是递归出口，仅对最后一个元素全排列，最后一个元素的全排列就是它本身，此时仅需打印整个数组$A[n]$。

  当$1<k<=n$时，按照上述的分析，应减小算法的规模，调用permutation(A, k-1, n)，生成后面$k-1$个元素的全排列。然后需要将数组$A[n-k]$元素和数组$A[n-k,n-1]$中的元素逐一互换，互换后执行permutation(A, k-1, n)。

#include <stdio.h>
#include <string.h>

int cnt=0;//计数器

void swap(char *a,char *b)
{
    char tmp;
    tmp=*a;
    *a=*b;
    *b=tmp;
}

void permutation(char *A,int k,int n)
{
    int i;
    if(k==1)//递归出口，此时打印整个数组。
    {
        cnt++;
        printf("第%2d种排列：",cnt);
        for(i=0;i<n;i++)
            printf("%c   ",A[i]);
        printf("\n");
    }
    else
    {
        for(int j=n-k;j<n;j++)
        {
            swap(&A[n-k],&A[j]);
            permutation(A,k-1,n);
            swap(&A[n-k],&A[j]);
        }
    }
}

int main()
{
    char ch[] = "ABCD";
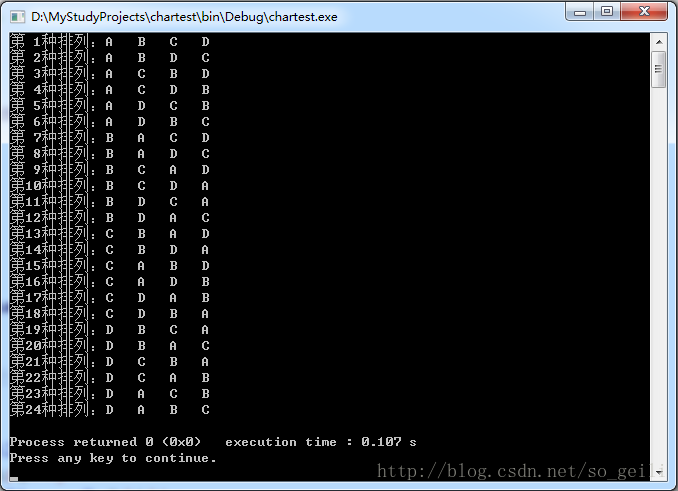
    permutation(ch,strlen(ch),strlen(ch));

    return 0;
}

执行结果如下：

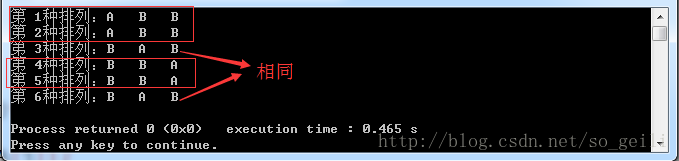
这样的方法没有考虑到重复元素的情况，如生成”ABB”全排列时：

======================

4.带重复元素的全排列的递归实现

  由于上述的全排列，在递归时就是从第一个元素起分别与它后面的元素逐一交换（没考虑重复元素）。所以当带重复元素时，这种方法就行不通了。

  例如：对122全排列时，第一个元素1与第二个元素2交换得到212；然后第一个元素1与第三个元素2交换，同样得到212，这种情况应该避免发生。所以在第一个元素与第三个元素交换之前，一定要检查第三个元素之前是否出现过，如果没有出现则执行交换；如果出现过则不进行交换。

  所以在全排列算法中，在递归实现时，应从第一个元素起分别与它后面的非重复元素交换。在编程实现时，在交换第i个元素与第j个元素之前，要求数组的$[i+1,j)$区间中的元素没有与第j个元素重复。下面给出完整代码：

#include <stdio.h>
#include <string.h>

typedef char bool;
#define false 0
#define true  1

int cnt=0;//计数器

void swap(char *a,char *b)
{
    char tmp;
    tmp=*a;
    *a=*b;
    *b=tmp;
}
//检查[from,to)之间的元素和第to号元素是否相同
bool isRepeat(char *A,int from,int to)
{
    bool flag=false;//初始为false，代表不重复元素
    for(int i=from;i<to;i++)
    {
        if(A[to]==A[i])
        {
            flag=true;
            return flag;
        }
    }
    return flag;
}

void permutation(char *A,int k,int n)
{
    int i;
    if(k==1)//递归出口，此时打印整个数组。
    {
        cnt++;
        printf("第%2d种排列：",cnt);
        for(i=0;i<n;i++)
            printf("%c   ",A[i]);
        printf("\n");
    }
    else
    {
        for(int j=n-k;j<n;j++)
        {
            if(!isRepeat(A,n-k,j))
            {
                swap(&A[n-k],&A[j]);
                permutation(A,k-1,n);
                swap(&A[n-k],&A[j]);
            }
        }
    }
}

int main()
{
    char ch[] = "122";
    permutation(ch,strlen(ch),strlen(ch));
    return 0;
}

执行结果如下：

======================

5.全排列的非递归实现（字典序）

非递归实现，也就是通常所说的字典序全排列算法。

首先，必须要理解字典序（dictionary order）。
第一种理解方式，按照纸质版字典的方式理解。第二种按照C语言中strcmp()函数的比较原理理解字典序。

例如：“abc”<“abcd”<“abde”<“afab”。

其次，如何求某一个排列紧邻着的后一个字典序。

设P是1～n的一个全排列:$P$=$p_1p_2......p_n$=$p1p2......p_{j-1}p_jp_{j+1} ......p_{k-1}p_kp_{k+1}......p_n$，求该排列的紧邻着的后一个字典序的步骤如下：

1. 从排列的右端开始，找出第一个比右边数字小的数字的序号$j$，即 $j=\max ( i |p_i<p_{i+1})$
2. 在$p_j$的右边的数字中，找出所有比$p_j$大的数中最小的数字$p_k$
3. 对换$p_j$和$p_k$
4. 再将$p_{j+1}......p_{k-1}p_kp_{k+1}...p_n$倒转得到排列p’=$p_1.....p_jp_n.....p_{k+1}p_kp_{k-1}.....p_{j+1}$，这就是排列p的下一个排列。

例如：p=839647521是数字1～9的一个排列。下面生成下一个排列的步骤如下：

1. 自右至左找出排列中第一个比右边数字小的数字4
2. 在该数字后的数字中找出比4大的数中最小的一个5
3. 将5与4交换，得到839657421
4. 将7421反转，得到839651247。这就是排列p的下一个排列。

以上这4步，可以归纳为：一找、二找、三交换、四翻转。和C++的 STL库中的next_permutation()函数（$\#include <algorithm>$）原理相同。

C代码实现如下：

#include <stdio.h>
#include <string.h>

typedef char bool;
#define false 0
#define true  1

int cnt=0;//计数器

void swap(char *a,char *b) {
    char tmp;
    tmp=*a;
    *a=*b;
    *b=tmp;
}
//冒泡升序排序
void BubbleSort(int arr[],int length) {
    int tmp;
    int i,j;
    for(i=length-1; i>0; i--) {
        for(j=0; j<i; j++) {
            if(arr[j] > arr[j+1]) {
                tmp=arr[j];
                arr[j]=arr[j+1];
                arr[j+1]=tmp;
            }
        }
    }
}

void PrintArray(int arr[],int length) {  //打印数组，用于查看排序效果
    printf("第%2d种排列为：[",++cnt);
    for(int i=0; i<length; i++) {
        if(i==length-1)
            printf("%d]\n",arr[i]);
        else
            printf("%d ,",arr[i]);
    }
}
void reverse(int arr[],int from, int to) {//反转[from,to]
    while(from < to) {
        char tmp = arr[from];
        arr[from]= arr[to];
        arr[to] = tmp;
        from ++;
        to --;
    }
}

bool Next_Permutation(int A[], int n) {
    int i,j,m;
    for(i = n-2; i >= 0; i--) { //一、找：
        if(A[i+1] > A[i])
            break;
    }
    if(i < 0)
        return false;//找不到，返回false
    m = i;
    i++;
    for( j=n-1; j>i; j--) {     //二、找
        if(A[j] >= A[m])
            break;
    }
    swap(&A[j],&A[m]);          //三、交换
    reverse(A,m+1,n-1);         //四、反转
    return true;
}

void Full_Permutation(int A[],int n) {
    if(A==NULL || n<=0) return; //健壮性检测
    BubbleSort(A,n);            //冒泡排序（升序）
    do {
        PrintArray(A,n);
    } while(Next_Permutation(A,n));//检测是否还有下一个字典序排列
}

int main() {
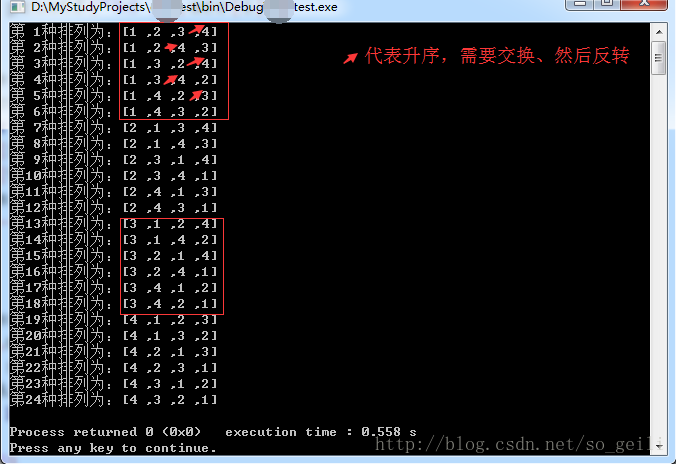
    int arr[]= {3,2,4,1};
    Full_Permutation(arr,sizeof(arr)/sizeof(int));
    return 0;
}

执行的结果为：

当测试数据中，含有重复元素时，仍然可以得到正确的全排列：

======================

6.递归算法时间复杂度分析

  全排列的递推关系式是：

$$T{(n)}= \begin{cases} O(1)， & 当 n=1\\ n T(n-1)，&当n>=2 \end{cases}$$

   所以不难算出，递归方式的全排列算法时间复杂度为$O(n!)$。

  注意：因为全排列一共有$n!$种，所以无论是递归实现，还是非递归实现，时间复杂度都是$O(n!)$。如果要对全排列进行输出，那么输出的时间要$O(n*n!)$。