线性代数感悟之8 生成空间和空间的基

引言

最近在看 liuyubobobo 的  线性代数 课，感觉很妙，有些感悟记录一下~~~

生成空间的定义

二维空间中的任何向量，都可以表示为u和v的线性组合，

我们说u和v可以生成整个二维空间。

N个向量是否可以生成整个空间？

这个过程其实是证明n维空间中n个向量可以表示其他任何向量u。

这个过程和证明线性相关的过程是一致的。注意这里的u表示任意的向量！

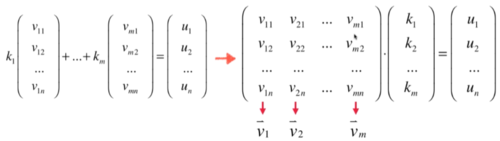
ps：整个过程使用列视角。

变化成这种形式之后，应该形成条件反射：

• 1 左边的v矩阵是系数矩阵，
• 2 k矩阵对应的是x未知数组成的矩阵，
• 3 u就是等式右边的结果组成的矩阵。
• 4 将v矩阵和u矩阵组成增广矩阵，当v变成单位矩阵的时候，u就变成了k的值

小结：

        证明N个向量是否可以生成整个空间？就是证明：n维空间中n个向量可以表示其他任何向量u。这就是其实就是证明：n维空间中n个向量是否和其他的任何向量线性相关。

那就是证明，这个矩阵是否有解：

又因为u是任意的向量，所以要考虑所有的情况（u不一定为零，不存在无数解的情况），这么就是求这个系数矩阵有唯一解，或者无解，如果有解就能生成空间，如果无解就是不能生成空间。 

那我们的环里又多了一环：

空间的基 

接下来，我们再看空间的基的概念（这里的基就是基础基本的意思）

如一组向量可以生成整个n为空间，且线性无关，这组向量一定有n个，则称这组向量为这个n维空间的一组基。

假设，m: 向量的个数，n：空间的维度

生成空间 的条件：m>=n

线性无关 的条件：m<=n

空间的基必须满足这两个条件。所以m必须等于n。

线性无关就是线性相关的否命题。

 这个是证明这个齐次方程组只有唯一的0解（也就是k全为0），这是证明线性无关的方法。

 最终你就会发现，证明Ax=0有唯一0解，和证明Ax=b有唯一解是一样的。

也就是说，如果n维空间的n个向量线性无关（Ax=0有唯一0解），那么就一定可以生成n维空间，那么就一定可以表示任意的向量，也就是Ax=b有唯一解！最后你发现只要A可逆，这些结论就都是成立的，由此可见可逆的重要性！

什么样的n个向量无法生成空间？

那么现在反过来思考，什么样的n个向量无法生成n维空间？也就是说，列向量由这n个向量组成的矩阵不可逆。那么什么样的矩阵不可逆呢？答案似乎已经呼之欲出了。

首先思考，什么样的n个向量无法生成n维空间？拿二维空间举类，任意两个不共线的向量都可以生成二维空间，反之，如果两个向量共线，则无法生成二维空间。这是直观的去看就能明白的。

如果v和u共线当然是无法生成空间的。

 如果二维空间中两条向量共线，也就是得到如下矩阵（注意这里使用列视角），这样得到的矩阵是无解的。

因为这样进行高斯消元下面一行 乘以x/y，下面一行就成了0行。明显无解了！

也就是说这样的矩阵是不可逆的。

扩展到四维空间：

1 0 3 0
0 1 5 0
0 0 0 0
0 0 0 1

比如这个矩阵，其中 1 2 3 列的向量不共线，但是共面，对于一个四维空间来说，它不是四维空间的一组基，也一定不可逆。

（感谢bobo老师的答疑）

矩阵不可逆的条件-慕课网 (imooc.com)

 123共面（共面也就是在一个二维空间里面），这里就说明123线性相关了，这就不满足空间的基的定义了，也就是说，这个矩阵不可逆。

那么从共线或者共面这个角度，也可以观察到矩阵是否可逆了。

回头再看这个例子：

u和v是二维空间的一组基，(2 ，2)，是系数K，(12，8) 是结果向量。

(2 ，2) 其实就是u和v这组基构建的空间中的值。而(12，8) 是对应的是标准正交基下的向量值。