原文链接: http://ufldl.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92
Softmax回归模型是logistic回归模型在多分类问题上的推广,在多分类问题中,类标签  可以取两个以上的值。由于 logistic 回归是针对二分类问题的,因此类标记
可以取两个以上的值。由于 logistic 回归是针对二分类问题的,因此类标记  。假设函数(hypothesis function) 如下:
。假设函数(hypothesis function) 如下:

我们将训练模型参数  ,使其能够最小化代价函数 :
,使其能够最小化代价函数 :

在 softmax回归中,类标  可以取
可以取  个不同的值。因此,对于训练集
个不同的值。因此,对于训练集  ,有
,有  。对于给定的测试输入
。对于给定的测试输入  ,我们想用假设函数针对每一个类别j估算出概率值
,我们想用假设函数针对每一个类别j估算出概率值  。也就是估计
。也就是估计  的每一种分类结果出现的概率。因此,假设函数
的每一种分类结果出现的概率。因此,假设函数 将要输出一个
将要输出一个  维的向量(向量元素的和为1)来表示这
维的向量(向量元素的和为1)来表示这  个估计的概率值,形式如下:
个估计的概率值,形式如下:

其中  是模型的参数。
是模型的参数。  这一项对概率分布进行归一化,确保所有概率之和为 1 。
这一项对概率分布进行归一化,确保所有概率之和为 1 。
softmax回归对应的代价函数公式(4)所示,其中 是指示函数。对于值为真的表达式,指数函数取值为1,反之为0。
是指示函数。对于值为真的表达式,指数函数取值为1,反之为0。
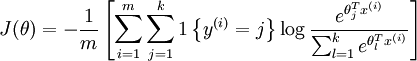
由于softmax回归模型是Logistic回归模型的一般形式,因此Logistic回归模型的代价函数也可以表示成这种形式:
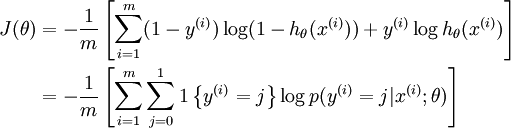
可以看到,Softmax代价函数与logistic 代价函数在形式上非常类似,只是在Softmax损失函数中对类标记的  个可能值进行了累加。
个可能值进行了累加。
对于  的最小化问题使用迭代的优化算法(例如梯度下降法,或 L-BFGS)。经过求导,得到梯度公式如下:
的最小化问题使用迭代的优化算法(例如梯度下降法,或 L-BFGS)。经过求导,得到梯度公式如下:
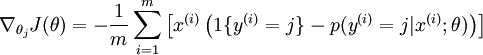
有了上面的偏导数公式以后,就可以将它代入到梯度下降法等算法中,来最小化  。 例如,在梯度下降法的标准实现中,每一次迭代需要进行如下更新:
。 例如,在梯度下降法的标准实现中,每一次迭代需要进行如下更新:
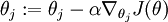 (
(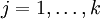 ) (7)
) (7)
在实际应用中,为了使算法实现更简单清楚,往往保留所有参数 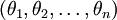 ,而不任意地将某一参数设置为 0。但此时需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。
,而不任意地将某一参数设置为 0。但此时需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。
通过添加一个权重衰减项 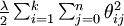 来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
-
![\begin{align}
J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }} \right]
+ \frac{\lambda}{2} \sum_{i=1}^k \sum_{j=0}^n \theta_{ij}^2
\end{align}](http://ufldl.stanford.edu/wiki/images/math/4/7/1/471592d82c7f51526bb3876c6b0f868d.png) (8)
(8)
有了这个权重衰减项以后 ( ),代价函数就变成了严格的凸函数,这样就可以保证得到唯一的解了。 此时的 Hessian矩阵变为可逆矩阵,并且因为
),代价函数就变成了严格的凸函数,这样就可以保证得到唯一的解了。 此时的 Hessian矩阵变为可逆矩阵,并且因为 是凸函数,梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。
是凸函数,梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。
为了使用优化算法,我们需要求得这个新函数  的导数,如下:
的导数,如下:
-
![\begin{align}
\nabla_{\theta_j} J(\theta) = - \frac{1}{m} \sum_{i=1}^{m}{ \left[ x^{(i)} ( 1\{ y^{(i)} = j\} - p(y^{(i)} = j | x^{(i)}; \theta) ) \right] } + \lambda \theta_j
\end{align}](https://i-blog.csdnimg.cn/blog_migrate/03807fc9155633938f50c35399539f5f.png) (9)
(9)
通过最小化 ,我们就能实现一个可用的 softmax 回归模型。
,我们就能实现一个可用的 softmax 回归模型。
























 2045
2045

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








