问题
从数字 1,2,3, ⋯ ,79,80 中任取 5 个互不相同的数,把这 5 个数相加之后,末位数字是 0,1,2, ⋯ ,8,或 9 的概率分别是多少?
乌克兰基辅大学(国立基辅塔拉斯-谢甫琴科国立大学)的一位统计和精算方向的谢甫琴科教授(2017年8月18日,哇,这个姓跟学校名字里的姓一模一样)给出了一种计算量很小的解法,可以通过一些既有的代数式子的系数,跟组合数之间的关系,经过一系列的对应关系和转化,求出相应的数字对应的频率数。所用代数式系数求组合数的方法,有点类似二项式系数跟组合数之间联系的方法,但是代数式比二项式复杂、不太常见、而且用到了多个关系式。不过这个得数学专业大学水平的才看得不吃力吧。 看别人给出的答案赏心悦目的同时,又有一种深深的自己智商零落尘土之后又被碾作泥的感觉。
分析
如果是有重复的放回,也就是允许 5 个取出的数有重复的情形,那么这就是一个等概率问题了。此时,从 1 到 80 的 80 个数中随机取 5 个,跟”从 1 到 10 的 10 个数字钟取 5 个,所得加和末位数字是 0,1, ⋯ ,9 的概率”,两个问题实际上是等价的。
对无放回的情况,先看一共有多少种组合Binomial[80,5]:
如果是等概率的,那么,10 个末位数字,每个平均分到的居然不是整数次,所以,显然不是这么算的了。
暴力解法
我发现自己求解这类问题喜欢用暴力解法,主要还是跟这类解法比较“直来直去”不是很消耗脑细胞有关。——偶尔会觉得其实是自己笨啊。
如果考场上不带计算器、不准用软件工具、没有网络和搜索引擎、各大资源网站服务器统统down机,所有电子资源统统无法访问,我这岂不是交白卷了?然而幸亏这只是如果。所以可以使用暴力手段。
首先,假设电脑的CPU主频够高,内存够大,这个问题的规模可以在普通电脑上直接计算。如果是老爷机、配置差,建议还是算了吧。
其次,我们用Mathematica计算这个问题。专门写一篇博客,主要是通过解决这个问题,又练习了下几个自己平时不太常用的函数的用法。记录一下,备查之用。
第一步,把所有的可能的 24,040,016 种组合全部列出来!就是这么霸气。但是,为了效率考虑,一定要在语句之后加上“;”,否则,在Notebook里面显示这么大量的数据,大内存的电脑估计一般也吃不消;
alist=Subsets[Range[80],{5}];这样就得到了全部的可能,然后把其中的每5个一组数字分别相加,得到一个 求和结果的数列:
slist=Total/@alist;因为只考虑末位数字,还得想办法把末位数字提取出来,生成一个新的数列:
nlist= (Last@IntegerDigits@#)&/@slist;然后我们要考察 0,1,2, ⋯ ,8,9 中每个末位数字出现的频率:
flist=Tally@nlist这样得到的结果就是包含每个数字及其出现的频率的数据列表了。
{{5, 2404008}, {6, 2404000}, {7, 2404000}, {8, 2404000}, {9, 2404000},
{0, 2404008}, {1, 2404000}, {2, 2404000}, {3, 2404000}, {4, 2404000}}
结果发现,出现 0 和 5 的概率居然稍微大于出现其它数字的概率。
结果
不过,为什么末位数字是 0 或 5 的概率大于其它数字?如何给自己一个合理的解释?? 为什么是 0 和 5,而不是其它数字?? 有没有什么定性、直观的解释呢?
观察一下,如果是从 1~80 中任取 4 个互不相同的数相加,所得到的和末位数字分别是 0~9 的频率分布又是怎样的呢?
计算就容易了,一共有多少种取法:
是不是刚好除以 10 每种数字尾数出现频率为 158158 次呢?
alist = Subsets[Range[80], {4}];
slist = Total /@ alist;
nlist = (Last@IntegerDigits@#) & /@ slist;
Tally@nlist得到:
{{0, 158236}, {1, 158080}, {2, 158236}, {3, 158080}, {4, 158236},
{5, 158080}, {6, 158236}, {7, 158080}, {8, 158236}, {9, 158080}}
同样是偶数或同为奇数时,出现的频率相同;出现偶数尾数的频率稍微大于出现奇数的频率。——看上去不科学。找不到简单直觉和定性的解释?
如果是从自1到99的自然数中任取7个,求和之后看末位数字分别是0,1,2,…,7,8,9的频数, 降低了计算量之后的暴力解法是这样的:
FullSimplify[Coefficient[((Total@(z^-# Product[(1+u z^n),{n,1,99}]/.z->(Exp[k I Pi/5]/.{k->Range[10]})))//ExpandAll//Collect[#, u] &), u^7]/10]&/@(Range[10]-1)结果是,0,1,2,…,7,8,9的频数:
0-> 1488705004,
1->1488701310,
2-> 1488704995,
3->1488701310,
4-> 1488704995,
5-> 1488701320,
6-> 1488704995,
7->1488701310,
8-> 1488704995,
9->1488701310
其它
推导一个复数运算,其实也还是练习组合使用一些相关的小工具和函数命令的技巧,
得到结果是(实际上如果坚持解析计算、反而只是把结果越变越复杂;而把待定的常数符号都变成特定的数值,这个过程才会是越来越简单的;——所以,每次看到问问题把数值问题以符号形式问的,都只能无奈;能够对自己的问题背景有了解、对解决问题所要达到的目标明确、对解决问题可能涉及的工具和解决到的深度有了解、对问题的描述足够独立清晰并提供背景相关的必要关键词而无须他人追问、常常只需要一些对解决方法或工具方面的简单提示,这样的提问者在国内论坛上比较少见):
虚部的分子
-\left({C_a}{C_c}{C_o}\omega\left(-{C_a}{C_c}\left({C_b}^2{R_b}^2\omega^2+1\right)\left({R_i}{R_s}\left({R_i}{C_i}^2+{C_s}^2{R_s}\right)\omega^2+{R_i}+{R_s}\right)-{C_a}{C_o}\left({C_b}^2{R_b}^2\omega^2+1\right)\left({R_i}{R_s}\left({R_i}{C_i}^2+{C_s}^2{R_s}\right)\omega^2+{R_i}+{R_s}\right)+{C_c}{C_o}\left({C_b}^2{C_i}{C_s}({C_i}{C_s}+{C_a}({C_i}+{C_s})){R_b}^2{R_c}{R_i}^2{R_s}^2\omega^6+\left({C_b}^2{C_i}({C_a}+{C_i}){R_b}^2{R_c}{R_i}^2-{C_a}{C_b}{C_i}^2{R_b}^2{R_s}{R_i}^2+{C_s}\left({C_b}^2({C_a}+{C_s}){R_c}{R_b}^2-{C_a}{C_b}{C_s}{R_i}{R_b}^2+{C_i}({C_i}{C_s}+{C_a}({C_i}+{C_s}))({R_b}+{R_c}){R_i}^2\right){R_s}^2\right)\omega^4+\left({C_b}^2{R_c}{R_b}^2-{C_a}{C_b}({R_i}+{R_s}){R_b}^2+({R_b}+{R_c})\left({C_i}({C_a}+{C_i}){R_i}^2+{C_s}({C_a}+{C_s}){R_s}^2\right)\right)\omega^2+{R_b}+{R_c}\right)\right)\right)实部的分子:
{C_c}{C_o}\left({C_a}^2\left({C_o}\left({C_b}^2{R_b}^2\omega^2+1\right)\left({C_i}\left({C_s}({C_i}+{C_s}){R_s}^2\omega^2+1\right){R_i}^2+{C_s}{R_s}^2\right)+{C_c}\left({C_o}\left({C_b}{R_b}^2{R_i}{R_s}\left({C_b}{R_c}{R_i}{C_i}^2+{C_b}{C_s}^2{R_c}{R_s}+({C_i}+{C_s})({C_i}{C_s}+{C_b}({C_i}+{C_s})){R_i}{R_s}\right)\omega^4+\left({C_b}^2({R_i}+{R_s})({R_c}+{R_i}+{R_s}){R_b}^2+{C_b}\left({C_i}{R_i}^2+{C_s}{R_s}^2\right){R_b}^2+{R_i}{R_s}\left(({R_b}+{R_c}){R_i}{C_i}^2+{C_s}^2({R_b}+{R_c}){R_s}+({C_i}+{C_s})^2{R_i}{R_s}\right)\right)\omega^2+({R_i}+{R_s})({R_b}+{R_c}+{R_i}+{R_s})\right)+\left({C_b}^2{R_b}^2\omega^2+1\right)\left({C_i}\left({C_s}({C_i}+{C_s}){R_s}^2\omega^2+1\right){R_i}^2+{C_s}{R_s}^2\right)\right)\right)\omega^2+{C_c}{C_o}\left({C_b}^2{R_b}^2\omega^2+1\right)\left({C_i}^2{R_i}^2\omega^2+1\right)\left({C_s}^2{R_s}^2\omega^2+1\right)+{C_a}\left({C_o}\left({C_b}^2{R_b}^2\omega^2+1\right)\left({C_i}^2{R_i}^2\omega^2+1\right)\left({C_s}^2{R_s}^2\omega^2+1\right)+{C_c}\left({C_b}{C_i}{C_s}(2{C_b}{C_o}{C_s}+{C_i}{C_o}{C_s}+{C_b}{C_i}(2{C_o}+{C_s})){R_b}^2{R_i}^2{R_s}^2\omega^6+\left({C_b}{C_i}({C_i}{C_o}+{C_b}({C_i}+2{C_o})){R_b}^2{R_i}^2+{C_s}\left({C_b}(2{C_b}{C_o}+({C_b}+{C_o}){C_s}){R_b}^2+{C_i}(2{C_o}{C_s}+{C_i}(2{C_o}+{C_s})){R_i}^2\right){R_s}^2\right)\omega^4+\left({C_b}^2{R_b}^2+{C_b}{C_o}{R_b}^2+{C_i}({C_i}+2{C_o}){R_i}^2+{C_s}(2{C_o}+{C_s}){R_s}^2\right)\omega^2+1\right)\right)\right)它们的分母:
{\left(\left(\left(\left({C_i}^2{C_s}^2({R_b}+{R_c})^2{R_i}^2{R_s}^2\omega^4+\left(2{C_i}{C_s}{R_i}^2{R_s}^2+{C_s}^2({R_b}+{R_c}+{R_i})^2{R_s}^2+{C_i}^2{R_i}^2({R_b}+{R_c}+{R_s})^2\right)\omega^2+({R_b}+{R_c}+{R_i}+{R_s})^2\right){C_o}^2+2{C_b}{R_b}^2\left({C_i}{C_s}({C_o}{C_s}+{C_i}({C_o}+{C_s})){R_i}^2{R_s}^2\omega^4+\left({C_i}({C_i}+{C_o}){R_i}^2+{C_s}({C_o}+{C_s}){R_s}^2\right)\omega^2+1\right){C_o}+2\left({C_i}\left({C_s}({C_i}+{C_s}){R_s}^2\omega^2+1\right){R_i}^2+{C_s}{R_s}^2\right){C_o}+{C_s}^2{R_s}^2+{C_i}^2{R_i}^2\left({C_s}^2{R_s}^2\omega^2+1\right)+{C_b}^2{R_b}^2\left({C_o}^2\left({C_i}^2{C_s}^2{R_c}^2{R_i}^2{R_s}^2\omega^4+\left(2{C_i}{C_s}{R_i}^2{R_s}^2+{C_s}^2({R_c}+{R_i})^2{R_s}^2+{C_i}^2{R_i}^2({R_c}+{R_s})^2\right)\omega^2+({R_c}+{R_i}+{R_s})^2\right)\omega^2+2{C_o}\left({C_i}\left({C_s}({C_i}+{C_s}){R_s}^2\omega^2+1\right){R_i}^2+{C_s}{R_s}^2\right)\omega^2+\left({C_i}^2{R_i}^2\omega^2+1\right)\left({C_s}^2{R_s}^2\omega^2+1\right)\right)\right)\omega^2+1\right){C_c}^2+2{C_o}\left({C_i}{C_s}({C_o}{C_s}+{C_i}({C_o}+{C_s})){R_i}^2{R_s}^2\omega^4+\left({C_i}({C_i}+{C_o}){R_i}^2+{C_s}({C_o}+{C_s}){R_s}^2\right)\omega^2+{C_b}{C_o}{R_b}^2\left({C_i}^2{R_i}^2\omega^2+1\right)\left({C_s}^2{R_s}^2\omega^2+1\right)\omega^2+{C_b}^2{R_b}^2\left({C_i}{C_s}({C_o}{C_s}+{C_i}({C_o}+{C_s})){R_i}^2{R_s}^2\omega^4+\left({C_i}({C_i}+{C_o}){R_i}^2+{C_s}({C_o}+{C_s}){R_s}^2\right)\omega^2+1\right)\omega^2+1\right){C_c}+{C_o}^2\left({C_b}^2{R_b}^2\omega^2+1\right)\left({C_i}^2{R_i}^2\omega^2+1\right)\left({C_s}^2{R_s}^2\omega^2+1\right)\right){C_a}^2+2{C_c}{C_o}\left({C_o}\left({C_b}^2{R_b}^2\omega^2+1\right)\left({C_i}^2{R_i}^2\omega^2+1\right)\left({C_s}^2{R_s}^2\omega^2+1\right)+{C_c}\left({C_b}{C_i}{C_s}({C_b}{C_i}{C_o}+{C_i}{C_s}{C_o}+{C_b}({C_i}+{C_o}){C_s}){R_b}^2{R_i}^2{R_s}^2\omega^6+\left({C_b}{C_i}({C_i}{C_o}+{C_b}({C_i}+{C_o})){R_b}^2{R_i}^2+{C_s}\left({C_b}({C_o}{C_s}+{C_b}({C_o}+{C_s})){R_b}^2+{C_i}({C_o}{C_s}+{C_i}({C_o}+{C_s})){R_i}^2\right){R_s}^2\right)\omega^4+\left({C_b}^2{R_b}^2+{C_b}{C_o}{R_b}^2+{C_i}({C_i}+{C_o}){R_i}^2+{C_s}({C_o}+{C_s}){R_s}^2\right)\omega^2+1\right)\right){C_a}+{C_c}^2{C_o}^2\left({C_b}^2{R_b}^2\omega^2+1\right)\left({C_i}^2{R_i}^2\omega^2+1\right)\left({C_s}^2{R_s}^2\omega^2+1\right)}附录
好东西都是别人的。
The question is about the sum of a M -subset of
{1,2,…,N−2,N−1,N} , taken modulo 10 .Yes, there are some tricky ways to enumerate those.
Denote εk=eπki/5 , k=1,…,9 , 10 th roots of unity. Then
∑k=09εnk={10,0,10∣n,10∤n.(1)Note that
F(u,z)=z−m∏j=1N(1+uzj)=∑j,nA(j,n)ujzn−m,
where A(j,n) is the number of j -subsets with sumn , and m∈0,1,2,⋯,7,8,9 is the last digit desired.
Therefore, the number of M -subsets with sum equal to0 modulo 10 is equal, thanks to (1) , to
[uM]110∑k=09F(u,εk),
(the coefficient before uM ).Let N=80 , If εk is a primitive root (i.e. k=1,3,7,9 ), then (noting that ε10k=1 )
F(u,εk)=z−m(∏n=09(1+uεnk))8=z−m(1−(−u)10)8=z−m(1−u10)8,
since εnk , n=0,…,9 , are different 10 th roots of unity.If k=2,4,6,8 , then εk is a primitive 5 th root of unity, so, similarly,
F(u,εk)=z−m(1−(−u)5)16=z−m(1+u5)16.
Further,
F(u,ε5)=z−m(1−(−u)2)40=z−m(1−u2)40.
Finally,
F(u,ε0)=F(u,1)(1+u)80.Therefore, form (the last digit) m=0 and the number of M=5 -subsets with sum divisible by 10 is
[uM=5]110(4(1−u10)8+4(1+u5)16+(1−u2)40+(1+u)80)=25(161)+110(805)=2404008.The number of M=4 -subsets:
[uM=4]110(4(1−u10)8+4(1+u5)16+(1−u2)40+(1+u)80)=110(402)+110(804)=158236.
If we were interested in the sum modulo some prime number, the computation would be much easier.











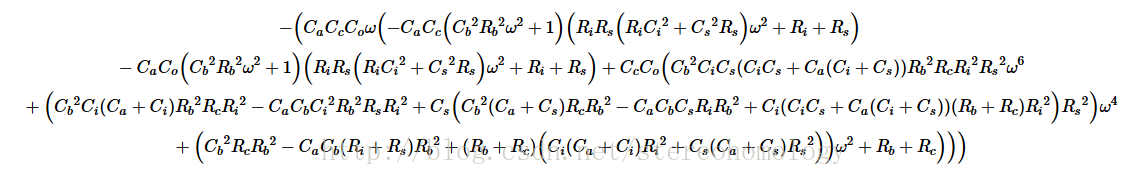
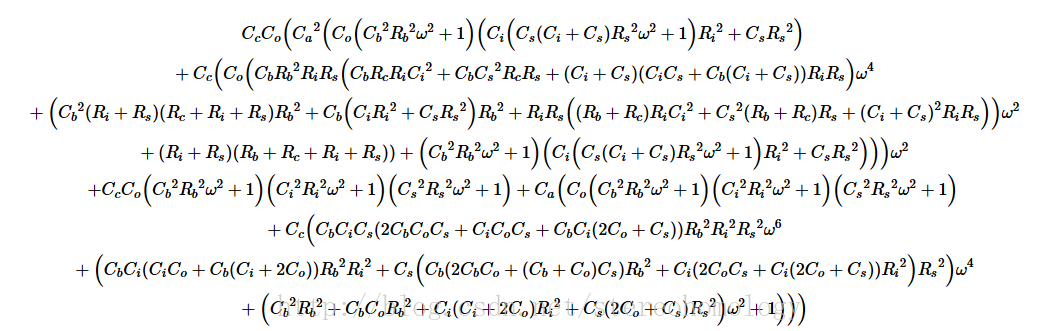
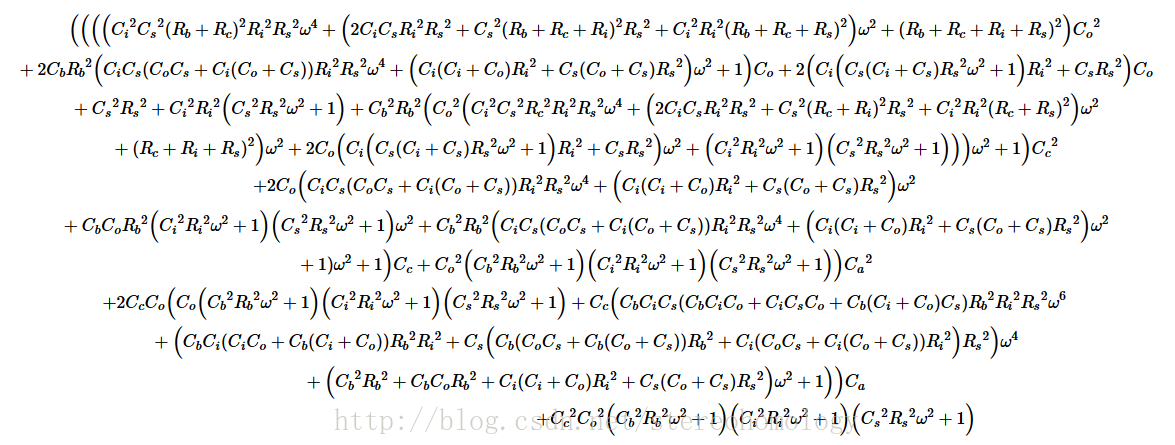














 421
421

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








