MCMC简介

一、重温贝叶斯公式

首先我们先复习一下贝叶斯公式：

$$P(\theta |x)=\frac{P(x|\theta )P(\theta )}{P(x)}$$

其中各项的说明如下：
$P(\theta |x)$：后验概率，给定观测数据$x$后，我们模型的参数$\theta$的概率，该项是我们最终想要获取的解；
$P(\theta )$ ：先验概率，在没有看到任何数据之前，我们对于模型参数$\theta$的猜想；
$P(x|\theta )$：似然，我们对数据分布的猜想；
$P(x)$：证据，也称为边缘似然，是我们遍历所有可能的$\theta$值后，得到的$x$观测值的概率的平均；

显然，对于大部分模型来说，$P(x)$是无法计算的，这也是贝叶斯公式在实际应用中存在的核心难点，即我们无法直接通过公式计算得到结果。
面对这种问题，一个很直观的想法是，那我们能否通过蒙特卡洛采样的方法来进行近似呢？很遗憾，直接对后验分布进行采样不仅同样需要通过贝叶斯公式来运算，而且还增加了一些逆向运算。
这个时候就只能搬出我们的救兵MCMC了。

二、MCMC的基本概念

MCMC的中文全称是马尔可夫链蒙特卡洛采样（Markov chain Monte Carlo），意为建立一个马尔可夫链来进行蒙特卡洛模拟 (constructing a Markov chain to do Monte Carlo approximation)。
其具体的做法是，构建一个可逆的马尔可夫链，并使得该链的状态转化概率与后验分布的概率分布一致。这样，在这个链上不断移动，我们就获得了想要的后验分布的随机样本。可逆的严格定义是：马尔可夫链必须满足细致平衡条件，即从状态$i$跳转到状态$j$的概率必须与从状态$j$跳转到状态$i$的概率相等。

以Metropolis-Hasting算法为例，简单介绍MCMC的工作流程：

1. 给参数$x_i$赋予一个初始值（随机数或经验值）。
2. 从某个简单对称的分布$Q(x_{i+1}|x_i)$中选一个新的值$x_{i+1}$，$Q$通常使用高斯分布或均匀分布。注：该步骤可理解为对状态$x_i$施加一个随机扰动。
3. 根据Metropolis-Hasting准则计算接受$x_{i+1}$的概率：$$p_{\alpha }(x_{i+1}|x_i)=min(1,\frac{p(x_{i+1})}{p(x_i)})$$
4. 从位于区间$[0,1]$内的均匀分布中随机取一个值，如果上一步骤中得到概率值大于该值，则接受新样本，否则仍保持原值。
5. 回到第2步重新迭代，直到我们有足够多的样本。

由上述流程可知，当$p(x_{i+1})>p(x_i)$时，算法一定会接受该样本，否则将以$\frac{p(x_{i+1})}{p(x_i)}$的概率接受该样本。显然，$p(x)$的计算是该算法的核心步骤，那对于一个实际的问题，$p(x)$要如何计算呢？

三、代码实现（Metropolis-Hasting 算法）

3.1 MCMC拟合数据分布

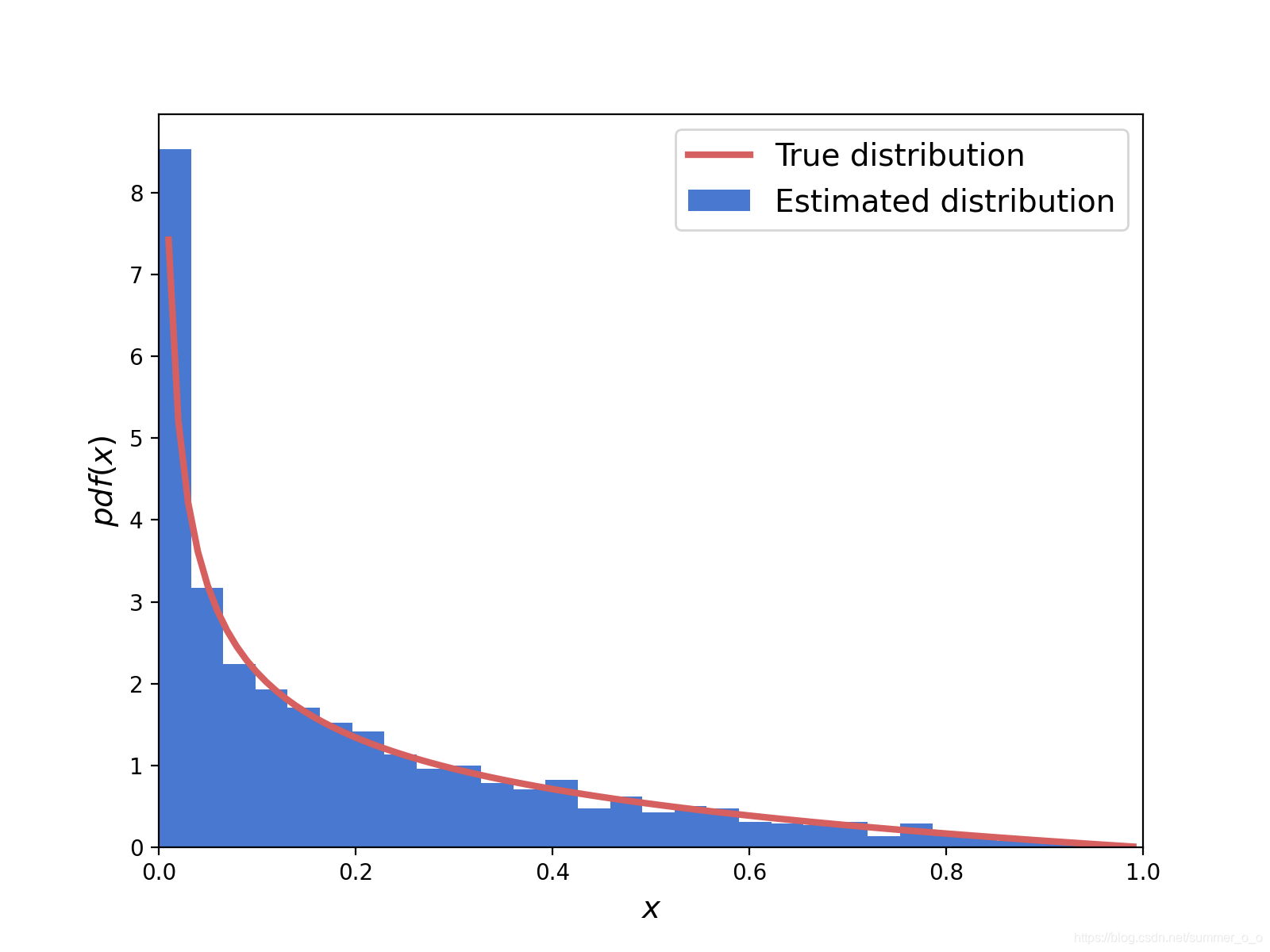
使用MCMC算法生成样本数据来拟合$Beta(0.5,2)$分布：

from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
palette = 'muted'
sns.set_palette(palette)
sns.set_color_codes(palette)


def metropolis1(func, steps=10000):
    samples = np.zeros(steps)
    old_x = func.mean()
    old_prob = func.pdf(old_x)

    for i in range(steps):
        new_x = old_x + np.random.normal(0, 0.5)
        new_prob = func.pdf(new_x)
        acceptance = new_prob/old_prob
        if acceptance >= np.random.random():
            samples[i] = new_x
            old_x = new_x
            old_prob = new_prob
        else:
            samples[i] = old_x
    return samples


np.random.seed(345)
func = stats.beta(0.5, 2)
samples = metropolis1(func=func)
x = np.linspace(0.01, .99, 100)
y = func.pdf(x)
plt.xlim(0, 1)
plt.plot(x, y, 'r-', lw=3, label='True distribution')
plt.hist(samples, bins=30, density=True, label='Estimated distribution')
plt.xlabel('$x$', fontsize=14)
plt.ylabel('$pdf(x)$', fontsize=14)
plt.legend(fontsize=14)
plt.show()

3.2 MCMC获取样本参数

假设x服从以下正态分布
$$\mu \sim Normal(0,1)$$ $$x|\mu \sim Normal(x;\mu ,1)$$

import numpy as np
from scipy.stats import norm


def sampler(data, samples=4, mu_init=.5, proposal_width=.5, mu_prior_mu=0, mu_prior_sd=1.):
    mu_current = mu_init
    posterior = [mu_current]
    for i in range(samples):
        # suggest new position
        mu_proposal = norm(mu_current, proposal_width).rvs()
        # Compute likelihood by multiplying probabilities of each data point
        likelihood_current = norm(mu_current, 1).pdf(data).prod()
        likelihood_proposal = norm(mu_proposal, 1).pdf(data).prod()
        # Compute prior probability of current and proposed mu
        prior_current = norm(mu_prior_mu, mu_prior_sd).pdf(mu_current)
        prior_proposal = norm(mu_prior_mu, mu_prior_sd).pdf(mu_proposal)
        p_current = likelihood_current * prior_current
        p_proposal = likelihood_proposal * prior_proposal
        # Accept proposal?
        p_accept = p_proposal / p_current
        # Usually would include prior probability, which we neglect here for simplicity
        accept = np.random.rand() < p_accept
        if accept:
            # Update position
            mu_current = mu_proposal
        posterior.append(mu_current)
    return np.array(posterior)

四、为什么MCMC是有效的？

让我们往回看一步，需要注意接受概率是整个事情有效的关键，通过先验与似然的乘积计算出的跳转概率与根据后验计算得到跳转概率是完全一致的：

$$\frac{P(\mu |x)}{P({\mu }_0|x)}=\frac{\frac{P(x|\mu )P(\mu )}{P(x)}}{\frac{P(x|{\mu }_0)P({\mu }_0)}{P(x)}}=\frac{P(x|\mu )P(\mu )}{P(x|{\mu }_0)P({\mu }_0)}$$

可以看到，我们无法计算的边缘项$P(x)$被约掉了，我们获得的跳转概率等同于通过后验计算得到，所以我们的参数会更多的在高概率密度的区域停留，而不是低概率密度的区域。