一、简介及作用
1、简介
- 正交实验法是一种设计实验的方法,目的是同时考虑多个因素对实验结果的影响,以确定各个因素之间的相互作用和最优的因素组合。
- 特点是通过有限次试验来获得全面和可靠的信息。它基于正交表,将多个因素的不同水平进行组合,保证各个因素之间相互独立,以避免因素间的干扰。通过改变不同因素的水平,可以观察和测量不同因素对实验结果的影响,进而确定最优的因素组合。
- 优势在于节省试验时间和成本,同时保证实验结果的可靠性和可重复性。它可以高效地确定影响因素,并找到最优的因素组合,以提高产品质量、优化工艺流程等。在品质管理、工程设计、产品开发等领域都有广泛的应用。
- 正交实验法是一种系统的、高效的实验设计方法,通过合理的样本选择和因素组合,可以同时考虑多个因素的影响,并确定最优的因素组合,以满足实验需求。
2、在测试中的作用
- 最大程度地覆盖测试场景:通过正交实验法,可以将多个因素的不同水平进行组合,从而生成一组最小的测试用例集合。这样可以确保测试覆盖面尽可能广泛,同时减少了测试用例的数量,节省了测试资源和时间。
- 发现不同因素间的相互影响:可以将不同因素进行独立组合,观察和测量不同因素对软件系统的影响。通过分析实验结果,可以确定不同因素之间的相互作用,从而帮助开发人员更好地理解和解决问题。
- 优化测试效果和资源利用:通过正交实验法,可以确定最优的因素组合,以提高软件系统的性能和质量。同时,正交实验法可以帮助测试人员在有限的资源条件下,更好地分配和利用测试资源,以获取最大的测试效果。
- 辅助决策和优化设计:正交实验法可以为软件系统的决策提供有力的支持。通过观察和分析正交实验的结果,可以确定不同因素对系统的影响程度,从而为系统的优化设计和决策提供指导。
由此可见,在测试用例设计期间,它帮助测试人员更好地设计测试用例,尽可能覆盖不同因素的组合,在确保覆盖的同时,减少测试用例的冗余,避免测试资源的浪费。
二、弱覆盖示例
1、测试场景示例
测试用例太多,怎么办?如何有效的控制测试用例的规模?
提到测试用例设计方法,我们一般优先会想到边界值法、等价类法、决策表法。这也都可以实现减少冗余用例这个用途,而且当输入数据之间存在关联性时,可以用决策表消除冗余。但 是,当输入域之间没有关联性的时候,该怎么做到控制这个规模。
如下的Web应用兼容性测试案例:
测试条件
- 操作系统:Windows,MacOS,Unix,Linux
- 浏览器:IE内核,FireFor内核,Chnome内核,Safari内核
- 分辨率:1920*1080,2560*1440,1600*900
这个测试的等价类全组合为:4*4*3=48,太多了,如何降低测试规模,并保证测试典型性?
我们现在能想到的方法是利用弱覆盖标准来设计等价类组合,
坐标轴演示
第一次覆盖:横轴为操作系统,有1、2、3、4四个值;纵轴为浏览器,有1、2、3、4四个值

- 现在就是覆盖到了8个组合条件(4+4=8)
- 这里用xy轴,暂时不引入第三个条件,因为引入第三个条件之后,就是三维空间了,不好控制。
- 弱覆盖标准下只需在这些数值交点上取相应组合就行,不重复的前提下最终得到4个组合,这四个组合再与另外一个条件进行第二次覆盖。当然可以随意取值,一个点就是两个变量,只要都覆盖到就可以
第二次覆盖:横轴为第一步取到的4种组合,分别设定为1、2、3、4;纵轴为分辨率,有1、2、 3三个值,弱覆盖标准下只需在这些数值交点上取相应组合就行;最终得到4个组合。覆盖7(4+3)个组合条件。这里x轴第四个重复了2k分辨率,不影响

最终的得到的组合:
- windows+IE内核+2560*1440
- MacOS+Chrome+1920*1080
- Unix+Firefor+1600*900
- Linux+Safari+2560*1440
但是,弱覆盖不能保证测试的结果安全性,所以以上这种方法并不可取。它没有覆盖到所有条件组合的关系,只覆盖到了原有的11个条件类,而没有覆盖到这11个类的组合。在等价类方面,为了确保测试用例的典型性,就要用到正交试验法。
三、正交表概念与使用
正交实验法也就是正交测试、正交表测试。起源于英国统计学专家R.A.Fisher,1920年提出正交实验法的基本思想。最终,日本的质量管理专家田口玄一,正式提出正交实验法,并将其广泛应用于工业试验。
正交测试的核心是正交表,L就表示正交表。由三个要素组成,公式: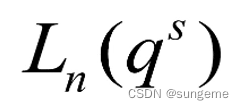
- 因素s: 输入条件 (因素)的个数(例如上个例子中,有三个条件,分别是操作系统,浏览器,分辨率)
- 水平q: 每个实验因素的取值个数、即每个因素的实验点的个数(也就是取值个数)
- 实验总个数n:表示测试用例的总个数,也就是这个正交表生产的测试用例的数目
上个例子的因素中,水平条件的只有操作系统和浏览器,都是4个条件,而分辨率只有3个条件,就可以使用混合水平正交表
图片中的公式表示的是等水平正交表,也就是每个因素的水平值相等。当因素的水平值不相等时我们应该使用混合水平正交表:
图解:

以上就是混合水平正交表的表达方式
但是混合表,一般来说在查表的时候,在系统里面查不到,很多情况下要借助等水平的正交表来做变换。首先要把n值(测试用例总数)算出来,因为查表的时候首先要知道n值是多少才能进行查表,要不然这个表不好查。
测试用例总数计算
- 如下这样一个等水平正交表,s=4、q=3、n=9
- 该例完全测试的用例总数是:条件1为3、条件2为3、条件3为3、条件4为3,总数 = 3*3*3*3=81
- 通过下列正交表简化,只剩下9个,并且已经设计好了每一个测试用例的等价类的组合方法

在这张表里可以看到,不同组合产生的用例结果为9,那9是怎么得来的
实际上,一个正交表的测试用例总数是有计算公式的:
ps:大写∑,下面的数字代表下界,即从哪里开始,上面的数字为上界,即在哪里结束。
等水平图解

最终公式就是L9(3^4)
混合水平图解
例如一开始的示例,操作系统和浏览器因素的q值(条件)分别都是4,而分辨率的q值(条件)是3
那么计算混合水平测试用例总数的方法就是:

最终也就是L9(4^2 * 3^1)
这9个用例既保证了测试用例的典型性,又保证了规模的大面积缩减,减少了大量冗余
四、正交表查询和处理
1、查询所需正交表
上例中,我们假设的输入条件s = L9的s值,取值个数q = L9的q值,这样可以在网络中找到L9的正交表设计(http://mathtt.com/consulting/odetable.pdf)
但是,并不是所有的正交表设计就刚好是可查询的正交表,比如上面的案例中,明显是一个混合水平正交实验,也无法查询到刚好使用的正交表
- 本例要进行正交实验,最少的实验次数 n = 1 +
(每个输入条件的取值个数-1),即:1+3+3+2=9,而上面的常用链接中,L9只有单水平的,显然不满足该例需求,因为输入条件个数和取值个数都不满足需求。
- 这时,就可以人为的进行q值的补充,使他们条件变宽,比如分辨率本来是3,其它两个都是4,那就可以认为的对分辨率加一个,使其变为4,就成为了n = 1+3+3+3 = 10 ,为:
。把范围扩大
- 因此,在参考中查询到 L16(
) ,该表的试验次数为16,显然大于该实验的最少需求9次,所以实验次数上满足需求,覆盖自己所需要的。
正交表:
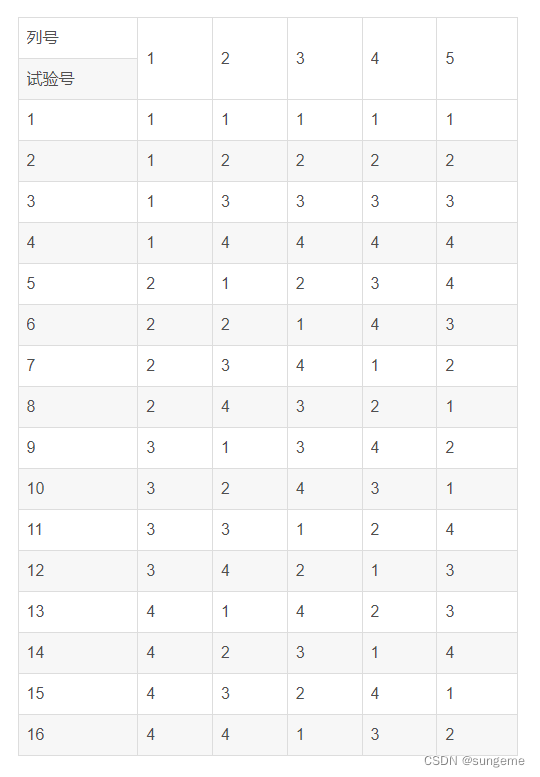
这样便覆盖了自己所需的范围,L9,三个类,每个类4个条件。因为是为了覆盖,选择了L16,虽然与自己算的L9相比会产生一定冗余,但是不会产生风险。在这张表中,只需要去掉第4、第5两列就行。问题是去掉了这两列,该表还是一个等水平正交表,并不是我们设计案例的混合水平正交实验,那该怎么办?
2、处理正交表
可以看案例的第3个输入条件(分辨率)只有3个取值,那就对该条件认为增加一个取值,如假设第4个取值也为1920*1080(因为这个分辨率是出现几率最高的,所以让它重复),这样这个实验就变成具有3个输入条件、每个条件4个取值的等水平正交实验了,这样就得到最终的、需要的正交表,如下:

但是第3列中的取值设了4,实际是没有4,分辨率只有三个取值,凭空设置一个分辨率也不现实,所以对于这一列中的4,自己可以任意取,转换为1\2\3都可以,不影响
以上就是通过人工进行一个处理,本来查不到的表,做了人工处理之后就可以得到想要的结果。实验次数是16次,比元素的全组合48次还是少了很多的,测试用例也很好的具备了典型性。
五、正交计算工具allpairs
1、下载

下载后解压至本地即可

2、使用
创建数据
可以先在Excel表格里面编辑需求条件:
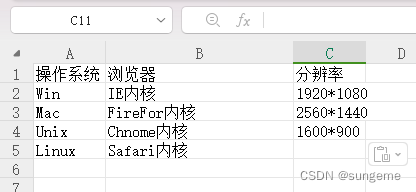
然后在allparis解压目录的根目录中创建一个txt文件:

把表格里面的内容复制粘贴到txt文件中:
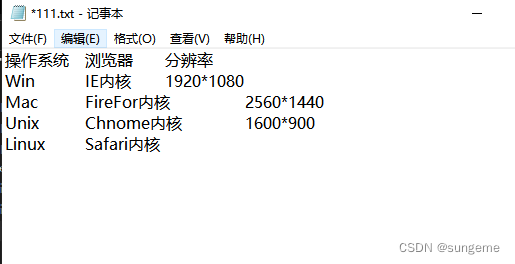
启动allpairs计算正交用例
allpairs.exe为命令执行程序,没有GUI界面,无法通过双击运行
上述步骤做好之后,在根目录中打开cmd
输入以下命令:
allpairs 111.txt > 222.txt
表示调用allpairs程序 将111.txt源数据 计算后输出到另外一个文件(222.txt)

如果没有报错,就代表生成成功了:
TEST CASES为生成的测试用例,下面是细节可以忽略。
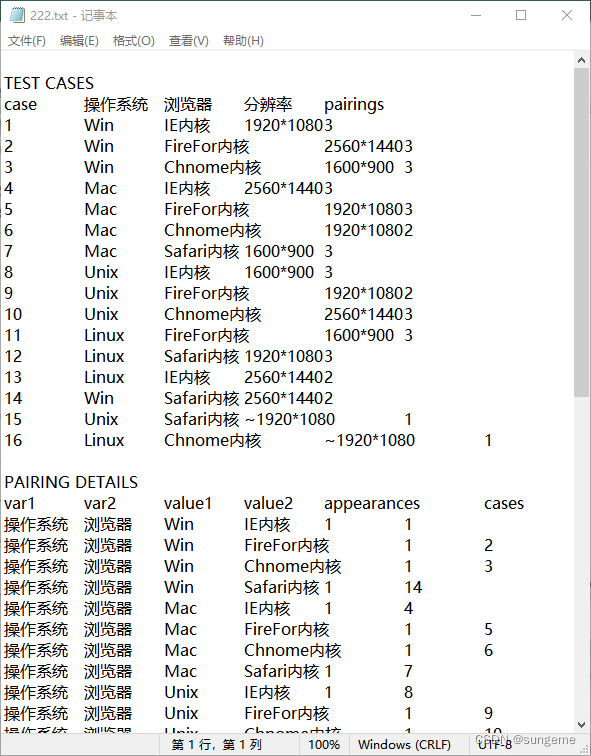
然后把TEST CASES中的内容复制到表格中:

ps:表格中可以看到~符号,这就是刚才自己计算的时候,假设的那一个值。这个值可以取任意,只要是分辨率条件里面有的值。
可以看到,刚刚自行查表,计算出来是16个,使用工具计算,也是16个。这样就得到测试用例
3、工具计算对比自行计算
也可以检查一下是否真的一致:
用序号代表取值:
- 操作系统:1、2、3、4
- 浏览器:1、2、3、4、
- 分辨率:1、2、3

结果:
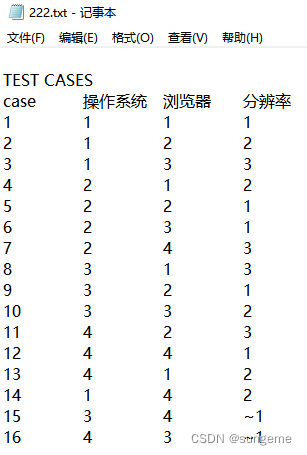
对比手动计算:
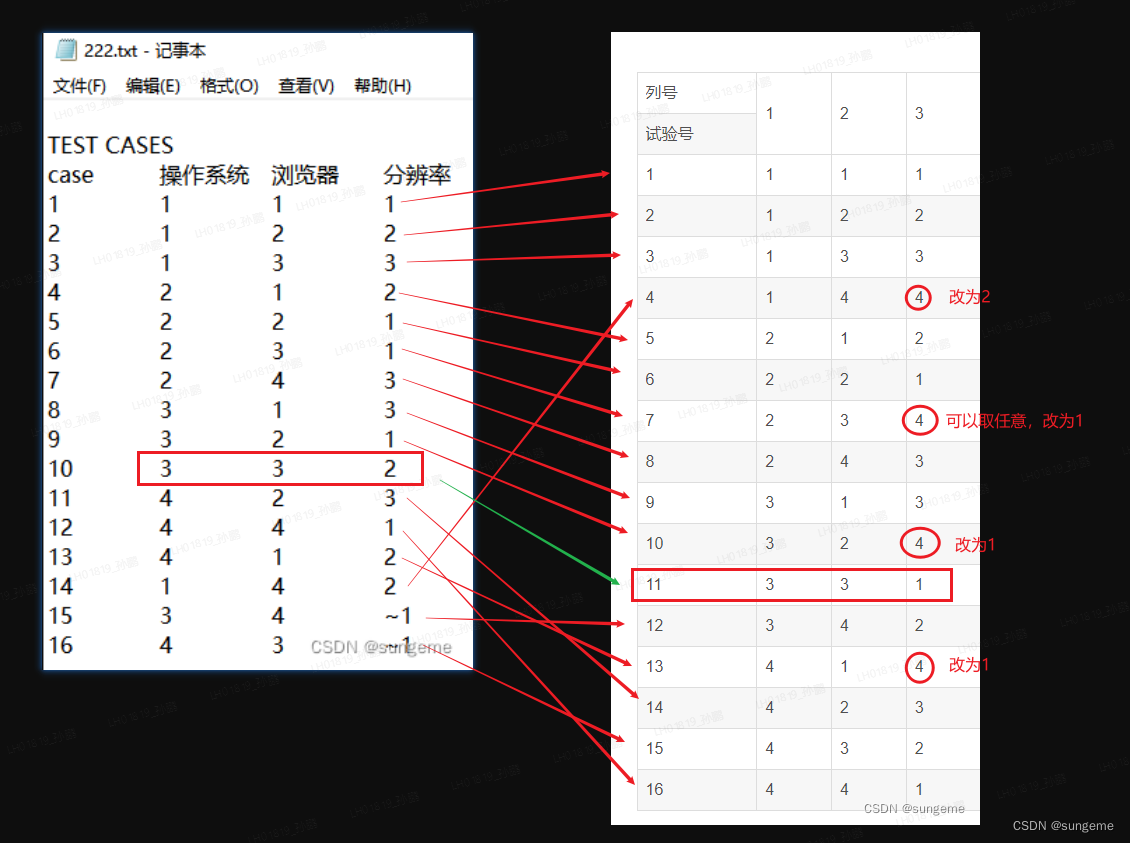
基本都是一致的,只有一个332和331不一致,因为根据统计学,2和1的出现频率可能是一致的,不过不影响。
证明通过查表和工具计算,得到的结果基本是一致的。就可以把111.txt和222.txt删掉了,保持原始包的干净,以备下次使用。



























 2250
2250

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








