算法基础3.1深度优先搜索(DFS)，宽度优先搜索(BFS)，树与图的存储，树与图的深度优先遍历，树与图的宽度优先遍历，拓扑排序

深搜dfs和宽搜bfs都可以对整个问题空间进行搜索，搜索的这个结构都是像一棵树一样，但是搜索的顺序是不一样的，深度优先搜索的话会尽可能往深了搜，当搜到叶结点的时候就会回溯，dfs可以看成是一个非常执着的人，他不管往哪条路走，一定会走到头，走不到头的时候是不可能回来的。一旦走到头了，注意回去的时候也不是说直接回到头，而是边回去边看能不能继续往前走。只有确定当前这个点所有的路都走不了的时候，才会往回退一步。宽度优先遍历bfs，比较像一个眼观六路，耳听八方的一个人，搜索的时候是一层一层搜的，也就是说可以同时看很多条路。它每一次只会扩展一层，不会离家太远，它是一层一层往外扩展的。只有周围这一层全部扩展完之后，才会去扩展下一层，这个是bfs的搜索的顺序。

来对比一下dfs和bfs，首先第一点是从使用的数据结构来看，dfs用的是栈stack。bfs，用的是队列quene。从使用的空间上来看，dfs往下搜的时候，只需要记住这一条路径上的所有点就可以了，因此它使用的空间是和我们高度成正比的，可以发现bfs每一次会把整个一层的所有结点都存下来。那么它所需要的空间是一个指数级别的，因此可以发现dfs在空间上是相比于bfs是有绝对优势的。就每一种方法都有好有坏，那再来看一下bfs的一个好处，它的好处就是由于bfs搜索的时候是一层一层往外扩展的，所以说他第一次搜到的点一定是最近的点，因此它有一个最短路的概念，如果要是每一条边的权重都是一，可以发现bfs第一次搜到的点一定是离我最近的一个点。但是dfs搜到的点不具有最短路的性质

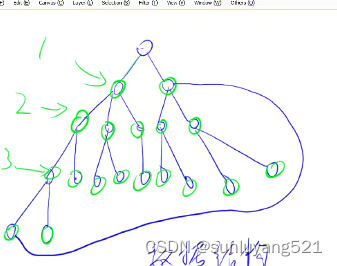
dfs来搜索这个点的距离就是三，bfs是可以搜到缩短距离为二。一个图的所有边的权重都是一的时候，bfs搜到的一定是最短路，因为扩展的时候是先把所有距离为一的点扩展进来，然后再把所有距离为二的点扩展进来，可以发现它是一层一层的，扩展的距离也是逐渐递增的。所以第一次扩展到的点一定是最近的点，这个是bfs一个很重要的特点，凡是涉及到什么最小步数，最短距离，问最少操作几次，基本上都是bfs。凡是算法的思路比较奇怪，或者是对空间要求比较高的，一般都用dfs来做。

DFS

dfs里面有两个很重要的概念，回溯和剪枝。刚开始学比较可能比较容易混淆，考虑dfs的时候，有一个很简单的方式，就是从搜索树的角度来考虑，每一个dfs都一定对应一条搜索树。

例题：

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式

共一行，包含一个整数 n。

输出格式

按字典序输出所有排列方案，每个方案占一行。

数据范围

1≤n≤7

输入样例：

3

输出样例：

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

dfs最重要的一个需要考虑的地方是顺序，dfs俗称暴搜，最重要的就是要把它的顺序想清楚，要用一个什么样的顺序，来把某一道题目的所有的方案全部遍历一遍。

全排列问题有很多种搜索顺序，这里用的搜索顺序是，假设一开始已经有n个空位了，比方说n=3，一开始有三个空位，顺序就是从第一位开始填，每一位就从前往后一位一位填，每一次填的时候，填的数字不能和前面一样就可以了，最开始的时候，三个都是空的，所以说最开始的状态就是三个空，那么那第一位一共有三种填法，分别对应三种不同的分支，第一个填法就是第一位填一，然后后面两位不填，第二种填法是第一位填二，后面两位不填，第三种填法是，第一位填三。第一位有三种不同填法，那就会走到不同的这个分支上，然后深搜会一层一层往下搜，第一层填完之后，会继续往下搜第二个位置，第二个位置其实也有三种方案，但是深搜的时候是不会把另外两个方向先画出来，直接一路走到黑，下一层，第一位已经确定是一，第二位枚举一下，首先第二位能填一吗？不可以，因为前面已经填过了。所以第二位只能填二，第三位空出来，这是第二层，然后深搜会一条道走到黑，是优先往下走的。是一个很执着的人，会优先往下走，那么还有一位空着的，所以说会继续往下走，它往下走的话，就只剩下第三位了，然后第三位就只剩下三可以填了，因此这个分支对应的方案就是123，然后把123输出就可以了。到123的时候，这个分支就已经无路可走了，那么这个执着的人就会往回退一步，可以发现，虽然有一位可以填，但是这一位只能填三，因此它只有这一条路可以走。所以说他现在也是没有路可以走了，那么他就继续再回溯一遍，再回到上一次的状态，注意它往回走的这个过程就叫回溯。然后走到这里之后，看一下这个分支是枚举的，第二位填二，然后这里可以发现还有第二条路可以走，就是第二位不光可以填二还可以填三。那么这个分支的话就是第二位填三的一个分支13，那么继续往下走就是132.同理，这条路就走完了，然后再回去，然后回去之后可以发现第二位的话只能填二或者三就已经无路可走了。那么这个人再回溯回到根结点，那就回到初始状态，初始状态第一位填一的这个分支，就已经走完了。所以说它就要枚举第一位填二的分支，以此类推，然后枚举第二位有两个分支，第一个分支，第二位可以填一，然后第三位是空，然后再往下走。那就是213，同理它第二位也可以填三，就231，然后走到三，看第二位也是有两种选法，第一个分支的话是31空，然后往下走的话就是312，第二个分支的话就是32空，然后往下走就是321。所以可以发现求全排列的这个过程是可以用dfs来做的，dfs搜索的顺序可以看成是一棵树。dfs其实就是递归，这个可以这么理解，不用把这个dfs和递归区分的太开，只要形式是这样的就可以被称为递归。

注意虽然看着像一棵树的形式，存的时候，每一次只会存当前这个路径，它只会存这一条路径，回溯的时候，它就没了，然后再往下走，它每次存的都是一条路径。其实不需要把整棵树存下来，而且也不需要真的把这个栈写出来，系统会做回溯的。就我们写的递归函数里面，系统是包含一个隐藏的栈来帮我们维护这个路径，咱们是不需要开额外的空间。

强调一点就是回溯的时候，比方说已经搜完这个分支了，当我们回溯的时候，回溯的时候一定要注意一点，就是恢复现场。就是从这个状态下去的时候什么样，回来的时候还得给人家恢复成什么样，就是用完的东西一定要放回去，这个是最重要的。因为往下搜的时候要看一下，就是往下搜的时候，其实不管从哪个点走到哪个分支，那走的时候这个分支看到的状态都是一样的，所以一定要记得恢复现场。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 10;
int n , path[N];  //path是用来存方案的
bool st[N]; // 需要知道当前这个位置上哪些数已经被用过了，=ture则被用过，状态数组

void dfs(int u ) // 第几个数字，一共几个数字
{
    if(u == n)// 递归到最后一个数字，叶节点
    {
        for (int i = 0; i < n; i ++ ) cout << path[i] << ' '; // 输出保存的结果
        puts(" ");   //输出空行
    }

    for (int i = 1; i <= n; i ++ )   //u<n的时候
        if (!st[i]) // 没有被用过的数
        {
            path[u] = i ;  //把i放到当前的位置上
            st[i] = true; // 记录i被用过
            dfs(u + 1);// 走到下一层
            st[i] = false;// 恢复现场
        }
}

int main()
{

    cin >> n;
    dfs(0);  //从0开始看
    return 0;

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/47087/
来源：AcWing

例题：n-皇后问题

n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

现在给定整数 n，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数 n。

输出格式

每个解决方案占 n行，每行输出一个长度为 n的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围

1≤n≤9

输入样例：

4

输出样例：

.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

第一种思路就是和搜索全排列的思路是一样的，n个皇后，每一行都要放一个皇后，而且只能放一个皇后，所以就可以从前往后看每一行，枚举每一行皇后放到哪一个位置，就是一个全排列的问题，这里一定要注意剪枝，可以按照完全按照上一个题的思路，先把n的全排列先全部生成出来，然后再判断这个方法是不是合法的，也可以边做边判断，假设当前这个位置要枚举某一个数的时候，假设枚举了一个四，就直接判断一下放在第三行的第四列放一个皇后之后有没有冲突？如果有冲突的话，就可以不用再往下走了。就可以看成是把这个树枝给剪掉了，这个过程就叫剪枝。

蓝色反对角线，绿色正对角线

代码分析：

对角线 dg[u+i]，反对角线udg[n−u+i]中的下标 u+i和 n−u+i 表示的是截距，上面分析中的(x,y)，相当于上面的(u,i)，反对角线 y=x+b, 截距 b=y−x，因为我们要把 b 当做数组下标来用，显然 b 不能是负的，所以我们加上 +n （实际上+n+4,+2n都行），来保证是结果是正的，即 y - x + n
而对角线 y=−x+b, 截距是 b=y+x，这里截距一定是正的，所以不需要加偏移量
核心目的：找一些合法的下标来表示dg或udg是否被标记过，所以如果你愿意，你取 udg[n+n−u+i]也可以，只要所有(u,i)对可以映射过去就行

作者：shwei
链接：https://www.acwing.com/solution/content/2820/
来源：AcWing

#include <iostream>
using namespace std;
const int N = 20;    //开两倍

// bool数组用来判断搜索的下一个位置是否可行
// col列，dg对角线，udg反对角线
// g[N][N]用来存路径

int n;
char g[N][N];
bool col[N], dg[N], udg[N];

void dfs(int u) {
    // u == n 表示已经搜了n行，故输出这条路径，找到一个方案
    if (u == n) {
        for (int i = 0; i < n; i ++ ) puts(g[i]);   // 等价于cout << g[i] << endl;
        puts("");  // 换行
        return;
    }

    // 枚举u这一行，搜索合法的列
    int x = u;
    for (int y = 0; y < n; y ++ )
        // 剪枝(对于不满足要求的点，不再继续往下搜索)  
        if (col[y] == false && dg[y - x + n] == false && udg[y + x] == false) {
            col[y] = dg[y - x + n] = udg[y + x] = true;//记录已经有皇后了
            g[x][y] = 'Q'; //放皇后
            dfs(x + 1);
            g[x][y] = '.';  // 恢复现场
            col[y] = dg[y - x + n] = udg[y + x] = false;
        }
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';

    dfs(0);

    return 0;
}   

作者：shwei
链接：https://www.acwing.com/solution/content/2820/
来源：AcWing

第二种方法：更为原始的枚举

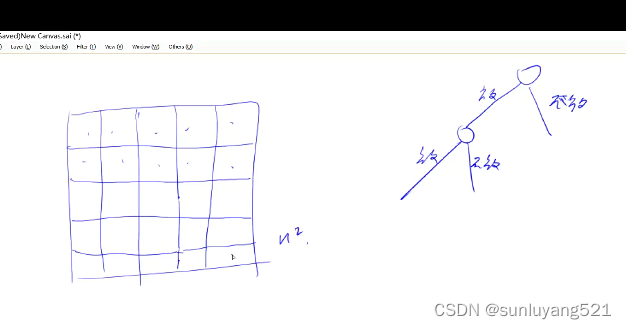
（DFS按每个元素枚举）时间复杂度O(2的n的平方的次方)
时间复杂度分析：每个位置都有两种情况，总共有 n2 个位置

// 不同搜索顺序 时间复杂度不同  所以搜索顺序很重要！
#include <iostream>
using namespace std;
const int N = 20;

int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N]; // 因为是一个个搜索，所以加了row

// s表示已经放上去的皇后个数
void dfs(int x, int y, int s)
{
    // 处理超出边界的情况
    if (y == n) y = 0, x ++ ;

    if (x == n) { // x==n说明已经枚举完n^2个位置了
        if (s == n) { // s==n说明成功放上去了n个皇后
            for (int i = 0; i < n; i ++ ) puts(g[i]);
            puts("");
        }
        return;
    }

    // 分支1：放皇后
    if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n])  //行，列，对角线，反对角线没有皇后

{
        g[x][y] = 'Q';
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
        dfs(x, y + 1, s + 1);
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;  //恢复现场
        g[x][y] = '.';
    }

    // 分支2：不放皇后
    dfs(x, y + 1, s);  //直接递归到下一个格子
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';

    dfs(0, 0, 0);

    return 0;
}

作者：shwei
链接：https://www.acwing.com/solution/content/2820/
来源：AcWing

BFS

宽搜最主要的一个优势就是可以搜到最短路，因为宽搜有一个很重要的性质，它是一圈一圈来往外搜索的，bfs先从窝边草开始吃，一层层往外吃。所以说宽搜里边搜到的所有点是一层一层来搜的，首先它先把所有距离为一的点全部搜到，这是第一层，然后第二层是把所有距离为二的点全部搜到。第三层就是把所有距离为三的点全部搜到。可以发现它搜索的时候啊。它搜到的点的距离，离当前的这个起点一定是越来越远的，因此第一次搜到的时候它的距离一定是最短的，因为如果要是以后再搜到的话，距离会更大，那就是第一次搜到的话，它的距离一定是最小的。这个有一个要求，就是这个图里边这个边的权重必须是一样的。

例题：走迷宫

给定一个 n×m 的二维整数数组，用来表示一个迷宫，数组中只包含 0或 1，其中 0表示可以走的路，1表示不可通过的墙壁。

最初，有一个人位于左上角 (1,1) 处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。

请问，该人从左上角移动至右下角 (n,m)处，至少需要移动多少次。

数据保证 (1,1)处和 (n,m)处的数字为 0，且一定至少存在一条通路。

输入格式

第一行包含两个整数 n和 m。

接下来 n行，每行包含 m 个整数（00 或 11），表示完整的二维数组迷宫。

输出格式

输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围

1≤n,m≤100

输入样例：

5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

输出样例：

8

广度优先遍历

思路：从起点开始，往前走第一步，记录下所有第一步能走到的点，然后从所有第一步能走到的点开始，往前走第二步，记录下所有第二步能走到的点，重复下去，直到走到终点。输出步数即可。

这就是广度优先遍历的思路

实现方式：广度优先遍历

用 g 存储地图，f存储起点到其他各个点的距离。
从起点开始广度优先遍历地图。
当地图遍历完，就求出了起点到各个点的距离，输出f[n][m]即可。

void bfs(int a, int b): 广度优遍历函数。输入的是起点坐标。
queue<PII> q;:用来存储每一步走到的点。
while(!q.empty())循环：循环依次取出同一步数能走到的点，再往前走一步。
int dx[4] = {0, 1, 0, -1}, dy[4] = {-1, 0, 1, 0};:一个点往下一步走得时候，可以往上下左右四方向走。

#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 110;
int g[N][N];//存储地图
int f[N][N];//存储每一个点到起点的距离
int n, m;
void bfs(int a, int b)//广度优先遍历
{
    queue<PII> q;
    q.push({a, b});
    //初始点的距离为 0.
    //可以不要这一句，因为f初始化的时候，各个点为0
    f[0][0] = 0;  //表示已经走过了
    while(!q.empty())  //队列不空
    {
        PII start = q.front();  //插入队头
        q.pop();  //弹出队头
        //这一句可以不要，因为入队的时候就置为了1
        g[start.first][start.second] = 1;

  int dx[4] = {0, 1, 0, -1}, dy[4] = {-1, 0, 1, 0};      
        for(int i = 0; i < 4; i++)//往四个方向走
        {
            //当前点能走到的点
            int x = start.first + dx[i], y = start.second + dy[i];
            //如果还没有走过
            if(g[x][y] == 0)
            {
                //走到这个点，并计算距离
                g[x][y] = 1;
                f[x][y] = f[start.first][start.second] + 1;//从当前点走过去，则距离等于当前点的距离+1.
                //这个点放入队列，用来走到和它相邻的点。
                q.push({x, y});
            }

        }
    }
    cout << f[n][m];  //输出右下点坐标
}

int main()
{
    memset(g, 1, sizeof(g));
    cin >> n >>m;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            cin >> g[i][j];
        }
    }
    bfs(1,1);

}

作者：Hasity
链接：https://www.acwing.com/solution/content/36520/
来源：AcWing

树和图的存储

一般来说树和图有两种存储方式，首先树是一种特殊的图，无环连通图。所以这里只讲图就可以了，图分成两种，分成有向图和无向图。有向图是说边是有方向的，a到b，无向图是说边是无方向的，如果给定ab这条边的话，意味着可以从a走到b。也可以从b走到a。

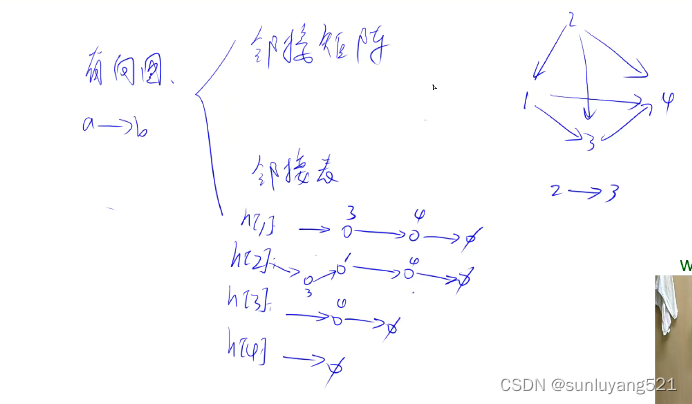
因此在算法题里面，如果说一个图是无向图，就建两条边就可以了，建一条a到b，再建一条b到a的就可以了。因此无向图就是一种特殊的有向图，所以说只需要考虑有向图如何存储就可以了。有向图的存储，一般有两大类，第一大类是用的比较少的邻接矩阵，开个二维数组g[ab]，存储a到b这条边的一个信息。它如果有权重的话，那gab就是这个权重，如果没有权重，那g[ab]就是一个布尔值，true表示有边，false表示没有边。如果有重边的话，这个邻接矩阵是不能存储重边的。如果有重边，就只能保留一条，因为如果要求最短路，就可以只保留一条最短的边，这个用的比较少，因为它比较浪费空间。它的空间复杂度是n方，比较适合存储稠密图。系数图就不是很好了，用的最多的是邻接表，就是之前讲过的单链表，如果有n个点的话，就开了n个单链表，每一个都是单链表，每一个节点上开了一个表。这个和拉链法存哈希表是一模一样的。每一个点上的单链表就是存这个点可以走到哪个点。

例题：树的重心

给定一颗树，树中包含 n 个结点（编号 1∼n）和 n−1 条无向边。

请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式

第一行包含整数 n，表示树的结点数。

接下来 n−1行，每行包含两个整数 a和 b，表示点 a 和点 b 之间存在一条边。

输出格式

输出一个整数 m，表示将重心删除后，剩余各个连通块中点数的最大值。

数据范围

1≤n≤10的5次方

输入样例

9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6

输出样例：

4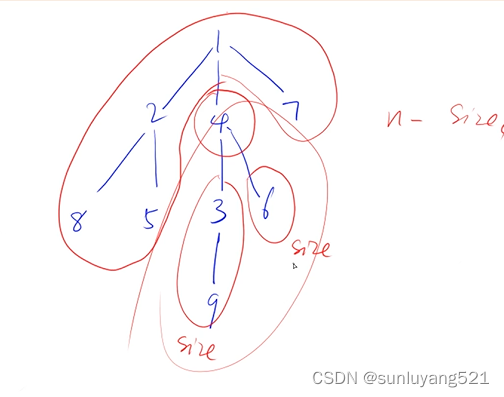

树是一种特殊的图，与图的存储方式相同。
对于无向图中的边ab，存储两条有向边a->b, b->a。
因此我们可以只考虑有向图的存储。

(1) 邻接矩阵：g[a][b] 存储边a->b

(2) 邻接表：

// 对于每个点k，开一个单链表，存储k所有可以走到的点。h[k]存储这个单链表的头结点
int h[N], e[N], ne[N], idx;

// 添加一条边a->b
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

// 初始化
idx = 0;
memset(h, -1, sizeof h);

作者：yxc
链接：https://www.acwing.com/blog/content/405/
来源：AcWing

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1e5 + 10; //数据范围是10的5次方
const int M = 2 * N; //以有向图的格式存储无向图，所以每个节点至多对应2n-2条边

int h[N]; //邻接表存储树，有n个节点，所以需要n个队列头节点
int e[M]; //存储元素的值
int ne[M]; //存储列表的next值
int idx; //单链表指针

//a所对应的单链表中插入b ， a作为根 
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

int main() {
    memset(h, -1, sizeof h); //初始化h数组n个头结点全部指向 -1表示尾节点

    return 0;
}

作者：松鼠爱葡萄
链接：https://www.acwing.com/solution/content/13513/
来源：AcWing

树和图的遍历

有两种方式，一种是深度优先遍历，一种是宽度优先遍历。只需要考虑有向图是如何遍历的就可以了。深度优先遍历就是逮住一个起点，然后从这个起点开始，一条道走到黑。

宽度优先遍历一层一层搜

树与图的遍历
时间复杂度 O(n+m)，n表示点数，m 表示边数

深度优先遍历

1) 深度优先遍历

int dfs(int u)
{
    st[u] = true; // st[u] 表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j]) dfs(j);
    }
}

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1e5 + 10; //数据范围是10的5次方
const int M = 2 * N; //以有向图的格式存储无向图，所以每个节点至多对应2n-2条边

int h[N]; //邻接表存储树，有n个节点，所以需要n个队列头节点
int e[M]; //存储元素的值
int ne[M]; //存储列表的next值
int idx; //单链表指针
int n; //题目所给的输入，n个节点
int ans = N; //表示重心的所有的子树中，最大的子树的结点数目

bool st[N]; //记录节点是否被访问过，访问过则标记为true

//a所对应的单链表中插入b ， a作为根 
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

// dfs 框架
/*
void dfs(int u){
    st[u]=true; // 标记一下，记录为已经被搜索过了，下面进行搜索过程
    for(int i=h[u];i!=-1;i=ne[i]){
        int j=e[i];  //j存当前链表里面的节点对应图里面边的编号是多少
        if(!st[j]) {  //如果没有被搜过
            dfs(j);
        }
    }
}
*/

//返回以u为根的子树中节点的个数，包括u节点
int dfs(int u) {
    int res = 0; //存储 删掉某个节点之后，最大的连通子图节点数
    st[u] = true; //标记访问过u节点
    int sum = 1; //存储 以u为根的树 的节点数, 包括u，如图中的4号节点

    //访问u的每个子节点
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        //因为每个节点的编号都是不一样的，所以 用编号为下标 来标记是否被访问过
        if (!st[j]) {
            int s = dfs(j);  // u节点的单棵子树节点数 如图中的size值
            res = max(res, s); // 记录最大联通子图的节点数
            sum += s; //以j为根的树 的节点数
        }
    }

    //n-sum 如图中的n-size值，不包括根节点4；
    res = max(res, n - sum); // 选择u节点为重心，最大的 连通子图节点数
    ans = min(res, ans); //遍历过的假设重心中，最小的最大联通子图的 节点数
    return sum;
}

int main() {
    memset(h, -1, sizeof h); //初始化h数组 -1表示尾节点
    cin >> n; //表示树的结点数

    // 题目接下来会输入，n-1行数据，
    // 树中是不存在环的，对于有n个节点的树，必定是n-1条边
    for (int i = 0; i < n - 1; i++) {
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a); //无向图，加入两条边
    }

    dfs(1); //可以任意选定一个节点开始 u<=n

    cout << ans << endl;

    return 0;
}

作者：松鼠爱葡萄
链接：https://www.acwing.com/solution/content/13513/
来源：AcWing

宽度优先遍历

(2) 宽度优先遍历 

queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);

while (q.size())
{
    int t = q.front();
    q.pop();

    for (int i = h[t]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true; // 表示点j已经被遍历过
            q.push(j);
        }
    }
}

作者：yxc
链接：https://www.acwing.com/blog/content/405/
来源：AcWing

例题：图中点的层次

给定一个 n个点 m 条边的有向图，图中可能存在重边和自环。

所有边的长度都是 1，点的编号为 1∼n。

请你求出 1号点到 n号点的最短距离，如果从 1 号点无法走到 n号点，输出 −1。

输入格式

第一行包含两个整数 n 和 m。

接下来 m 行，每行包含两个整数 a和 b，表示存在一条从 a 走到 b 的长度为 1 的边。

输出格式

输出一个整数，表示 1 号点到 n 号点的最短距离。

数据范围

1≤n,m≤10的5次方

输入样例：

4 5
1 2
2 3
3 4
1 3
1 4

输出样例：

1

判断1号节点能否走到n号节点，广度优先遍历即可。

思路：

用 dist 数组保存1号节点到各个节点的距离，初始时，都是无穷大。

用 st 数组标记各个节点有没有走到过。

从 1 号节点开始，广度优先遍历：

1 号节点入队列，dist[1] 的值更新为 0。

如果队列非空，就取出队头，找到队头节点能到的所有节点。如果队头节点能到走到的节点没有标记过，就将节点的dist值更新为队头的dist值+1，然后入队。

重复步骤 2 直到队列为空。

这个时候，dist数组中就存储了 1 号节点到各个节点的距离了。如果距离是无穷大，则不能到达，输出 -1，如果距离不是无穷大，则能到达，输出距离。

图的存储：邻接表

用 h 数组保存各个节点能到的第一个节点的编号。开始时，h[i] 全部为 -1。

用 e 数组保存节点编号，ne 数组保存 e 数组对应位置的下一个节点所在的索引。

用 idx 保存下一个 e 数组中，可以放入节点位置的索引

插入边使用的头插法，例如插入：a->b。首先把b节点存入e数组，e[idx] = b。然后 b 节点的后继是h[a]，ne[idx] = h[a]。最后，a 的后继更新为 b 节点的编号，h[a] = idx，索引指向下一个可以存储节点的位置，idx ++ 。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;

const int N = 100010;

int h[N],ne[N], e[N], idx;//邻接表数据结构
int dist[N];//存储距离
int st[N];//标记点是否走到过
int n, m;

void add(int a, int b)//邻接表存储图，插入函数
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void bfs()
{
    memset(dist, 0x3f, sizeof(dist));//初始都没有走到过，距离无穷大
    dist[1] = 0;//从1号节点开始，距离为0
    queue<int> q;//队列
    q.push(1);//1号节点入队列
    st[1] = 1;//1到1的距离为0，已经求出
    while(q.size())//对列非空，就一直往后搜索
    {
        int t = q.front();//队头出队，找该点能到的点
        q.pop();
        for(int i = h[t]; i != -1; i = ne[i])//遍历所有t节点能到的点，i为节点索引
        {
            int j = e[i];//通过索引i得到t能到的节点编号
            if(!st[j])//如果没有遍历过
            {
                dist[j] = dist[t] + 1;//距离为t号节点的距离+1
                q.push(j);//节点入队
                st[j] = 1;//入队后标记，已经遍历过了
            }
        }
    }
}

int main()
{
    cin >> n >>m;
    memset(h, -1, sizeof h);//初始化，所有节点没有后继，后继都是-1
    for(int i = 0; i < m; i++)//读入所有边
    {
        int a, b;
        cin >> a >> b;
        add(a, b);//加入邻接表
    }
    bfs();//广度优先遍历

    cout << (dist[n] == 0x3f3f3f3f ? -1 : dist[n]);//如果到n号节点的距离不是无穷大，输出距离，如果是无穷大，输出-1.
    return 0;
}

作者：Hasity
链接：https://www.acwing.com/solution/content/45573/
来源：AcWing

拓扑排序

拓扑排序是图的宽搜的一种应用，是针对有向图的，排完序后所有指向都是从左向右，环无法进行，因为环一定存在从后指向前的边，一个有向无环图一定至少存在一个入度为0的点，可用反证法证必有两点存在相同，可以把这个入度为0的点作为突破口，逐步删去与它有关联的点，可证一个有向无环图一定存在拓补序列，也被称为拓补图

一个点的入度是指有多少条边指向自己，出度是指有几条边出去，入度为0就意味着不会有任何一条点在我前面，因此所有入度为0的点都可以排在当前最前面的位置。因此第一步就是把所有入度为0的点入队，后面宽搜

一个有向图，如果图中有入度为 0 的点，就把这个点删掉，同时也删掉这个点所连的边。

一直进行上面出处理，如果所有点都能被删掉，则这个图可以进行拓扑排序。一个图的拓补序不唯一。

举例子

开始时，图是这样的状态，发现A的入度为 0，所以删除A和A上所连的边，结果如下图：

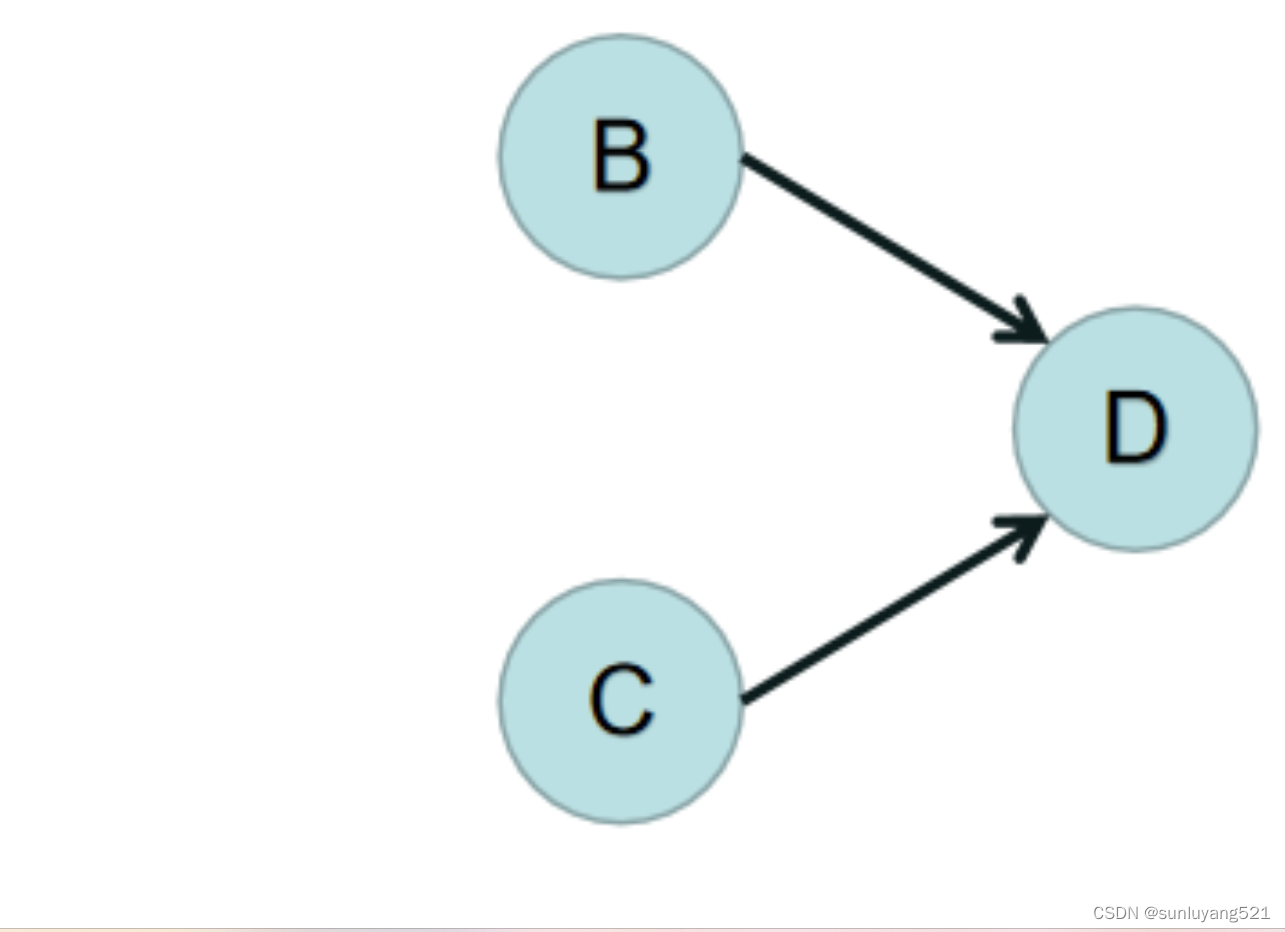
这时发现B的入度为 0，C的入度为 0，所以删除B和B上所连的边、C和C上所连的边，结果如下图：

这时发现发现D的入度为 0，所以删除D和D上所连的边(如果有就删)，结果如下图：

这时整个图被删除干净，所有能进行拓扑排序。

例题：有向图的拓补序列

给定一个 n 个点 m 条边的有向图，点的编号是 1到 n，图中可能存在重边和自环。

请输出任意一个该有向图的拓扑序列，如果拓扑序列不存在，则输出 −1。

若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x 在 A 中都出现在 y之前，则称 A是该图的一个拓扑序列。

输入格式

第一行包含两个整数 n 和 m。

接下来 m行，每行包含两个整数 x 和 y，表示存在一条从点 x到点 y的有向边 (x,y)。

输出格式

共一行，如果存在拓扑序列，则输出任意一个合法的拓扑序列即可。

否则输出 −1。

数据范围

1≤n,m≤10的5次方

输入样例：

3 3
1 2
2 3
1 3

输出样例：

1 2 3

解题思路

首先记录各个点的入度

然后将入度为 0 的点放入队列

将队列里的点依次出队列，然后找出所有出队列这个点发出的边，删除边，同事边的另一侧的点的入度 -1。

如果所有点都进过队列，则可以拓扑排序，输出所有顶点。否则输出-1，代表不可以进行拓扑排序。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int e[N], ne[N], idx;//邻接表存储图
int h[N];
int q[N], hh = 0, tt = -1;//q队列保存入度为0的点，也就是能够输出的点，hh队头，tt队尾
int n, m;//保存图的点数和边数
int d[N];保存各个点的入度

void add(int a, int b){  //插入模板
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void topsort(){ //拓补排序
    for(int i = 1; i <= n; i++){//遍历一遍顶点的入度。
        if(d[i] == 0)//如果入度为 0, 则可以入队列
            q[++tt] = i;
    }
    while(tt >= hh){//循环处理队列中点的
        int a = q[hh++];  //每次取出来队头元素
        for(int i = h[a]; i != -1; i = ne[i]){//循环删除 a 发出的边
            int b = e[i];//a 有一条边指向b，找到出边
            d[b]--;//删除边后，b的入度减1
            if(d[b] == 0)//如果b的入度减为 0,则 b 可以输出，入队列
                q[++tt] = b;
        }
    }
    if(tt == n - 1){//n-1说明一共进了n个点，如果队列中的点的个数与图中点的个数相同，则可以进行拓扑排序
        for(int i = 0; i < n; i++){//队列中保存了所有入度为0的点，依次输出
            cout << q[i] << " ";
        }
    }
    else//如果队列中的点的个数与图中点的个数不相同，则可以进行拓扑排序
        cout << -1;//输出-1，代表错误
}

int main(){
    cin >> n >> m;//保存点的个数和边的个数
    memset(h, -1, sizeof h);//初始化邻接矩阵
    while (m -- ){//依次读入边
        int a, b;
        cin >> a >> b;
        d[b]++;//顶点b的入度+1
        add(a, b);//添加到邻接矩阵
    }
    topsort();//进行拓扑排序
    return 0;
}

作者：Hasity
链接：https://www.acwing.com/solution/content/103954/
来源：AcWing

end——————————————————————————————————————————