1088 最长回文子串

1088 最长回文子串 

基准时间限制：1 秒 空间限制：131072 KB 分值: 0  难度：基础题

 收藏

 关注

回文串是指aba、abba、cccbccc、aaaa这种左右对称的字符串。

输入一个字符串Str，输出Str里最长回文子串的长度。

Input

输入Str（Str的长度 <= 1000)

Output

输出最长回文子串的长度L。

Input示例

daabaac

Output示例

5

基于manacher算法的一种方法，如果数据过大不可行

manacher看这个->1089 最长回文子串 V2（Manacher算法）

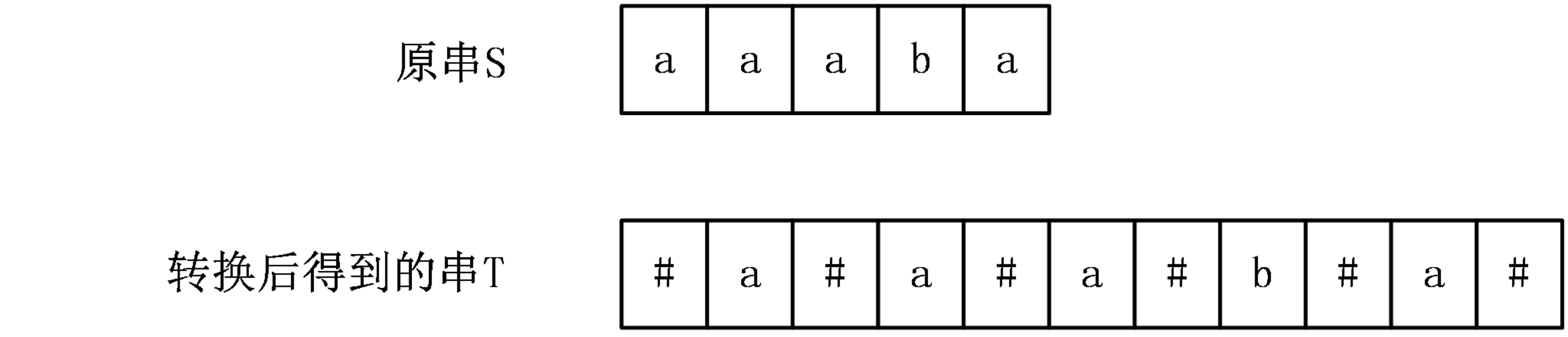
首先，Manacher算法提供了一种巧妙地办法，将长度为奇数的回文串和长度为偶数的回文串一起考虑，具体做法是，在原字符串的每个相邻两个字符中间插入一个分隔符，同时在首尾也要添加一个分隔符，分隔符的要求是不在原串中出现，一般情况下可以用#号。下面举一个例子：

                                         1    2    3    4   5    6   7    8   9   10   11

       

Manacher算法用一个辅助数组Len[i]表示以字符T[i]为 中心 的最长回文子串的 最右字符到T[i]的长度 。

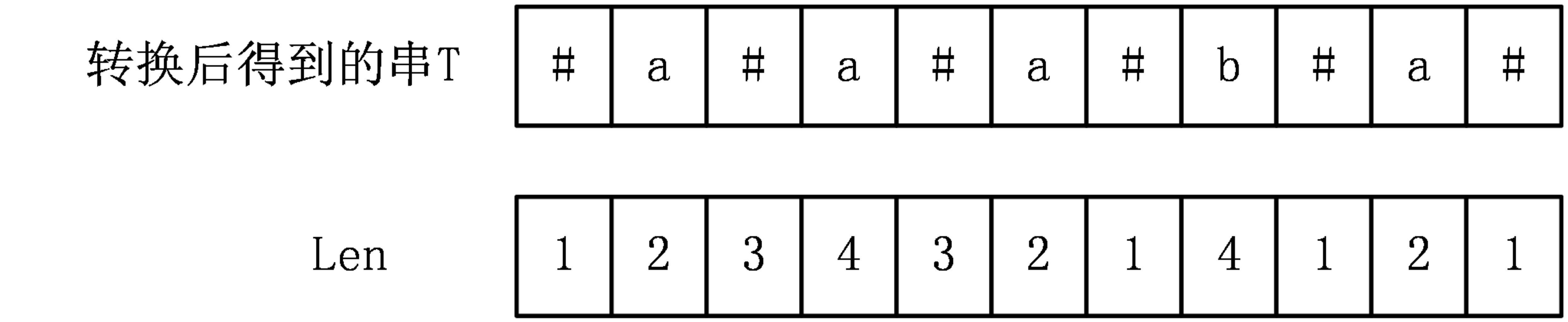
比如：len[8]=4->  以b为中心的最长回文子串是#a#b#a#，从最右字符到b长度为4。

对于上面的例子，可以得出Len[i]数组为:

 

对于以T[i]为中心的最长回文字串，其长度就为2*Len[i]-1。（len[8]->4*2-1）

经过观察可知，T中所有的回文子串，其中#的数量一定比其他字符的数量多 1，也就是有Len[i]个分隔符，剩下Len[i]-1个字符来自原字符串，所以该回文串在原字符串中的长度就为Len[i]-1。

有了这个性质，那么原问题就转化为求所有的Len[i]。

设每次len[i]为j。

还是以len[8] （#a#b#a#） 为例：

记i为最长回文子串中心在T中的位置，i=8。初始j=1。

if(s[i-j]==s[i+j]) j++;  //关键代码

解析：i=8,j=1—>s[7]==s[9]  j=2;

        i=8,j=2—>s[6]==s[10]  j=3;

        i=8,j=3—>s[5]==s[11]  j=4;

由上可知，每次j++，就是由中心位置向两边继续扩，如果两边相等，继续向外扩。

一共可以向外扩多少，说明两边相同的字符有多少对，再加上中心（j的初始值1），最后j的值就是该中心值len[]。

代码：

#include<iostream>
#include<cstring>
using namespace std;

char str[12000];
char s[12000];

int main()
{
	cin>>str;
    int i,j,maxx=1,temp;
    int n=strlen(str);
    for(i=n;i>=1;i--)
    {
        s[i*2+1]='#';
        s[i*2]=str[i-1];
    }
    s[0]=s[1]='#';
    n=strlen(s);
    for(i=2;i<n;i++)
    {
        j=1;
        while(s[i-j]==s[i+j]&&i-j>=1&&i+j<n)
            j++;
        temp=j-1;
        if(temp>maxx)
            maxx=temp;
    }
    cout<<maxx<<endl;
	return 0;
}