寻找危险因素:寻找某一疾病的危险因素等;
预测:根据模型,预测在不同的自变量情况下,发生某病或某种情况的概率有多大;
自变量既可以是连续的,也可以是分类的。
常规步骤
- 寻找h函数(即hypothesis):需要找的分类函数,它用来预测输入数据的判断结果;
- 构造Cost函数(损失函数):该函数表示预测的输出(h)与训练数据类别(y)之间的偏差;
- 构造J函数(J(θ)函数):将Cost求和或者求平均,表示所有训练数据预测值与实际类别的偏差。
- 想办法使得J函数最小并求得回归参数(θ)。
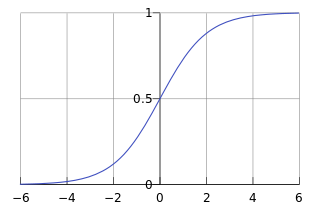
- 构造预测函数h:
-
-
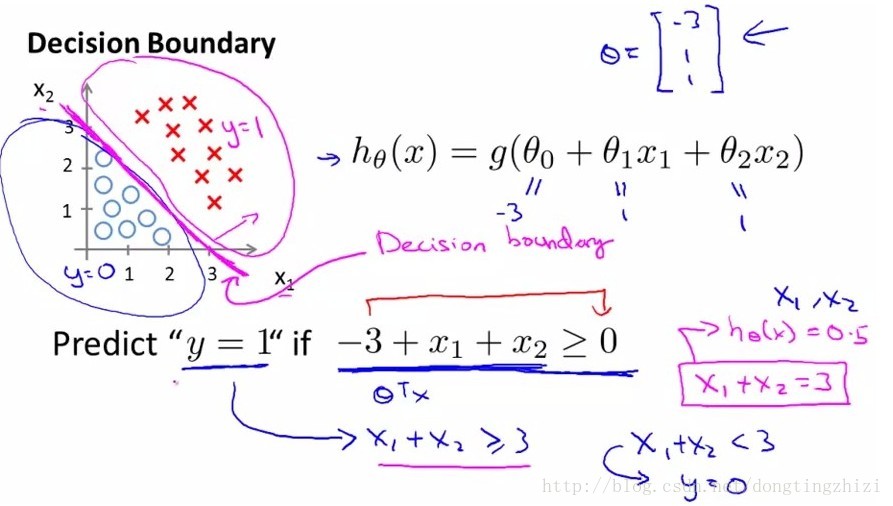
- 下面左图是一个线性的决策边界,右图是非线性的决策边界。
-
-
-
对于线性边界的情况,边界形式如下:
构造预测函数为:
函数
的值有特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
构造Cost函数
Cost函数和J函数如下,它们是基于最大似然估计推导得到的。
下面详细说明推导的过程:
(1)式综合起来可以写成:
取似然函数为:
对数似然函数为:

最大似然估计就是求使 取最大值时的θ,其实这里可以使用梯度上升法求解,求得的θ就是要求的最佳参数。但是,在Andrew Ng的课程中将
取最大值时的θ,其实这里可以使用梯度上升法求解,求得的θ就是要求的最佳参数。但是,在Andrew Ng的课程中将 取为下式,即:
取为下式,即:

因为乘了一个负的系数-1/m,所以取 最小值时的θ为要求的最佳参数。
最小值时的θ为要求的最佳参数。
梯度下降法求的最小值
θ更新过程:


上式求解过程中用到如下的公式:
θ更新过程可以写成:

约定训练数据的矩阵形式如下,x的每一行为一条训练样本,而每一列为不同的特称取值:

g(A)的参数A为一列向量,所以实现g函数时要支持列向量作为参数,并返回列向量。由上式可知 可由
可由 一次计算求得。
一次计算求得。
θ更新过程可以改为:

综上所述,Vectorization后θ更新的步骤如下:
(1)求 ;
;
(2)求 ;
;
(3)求  。
。
代码分析
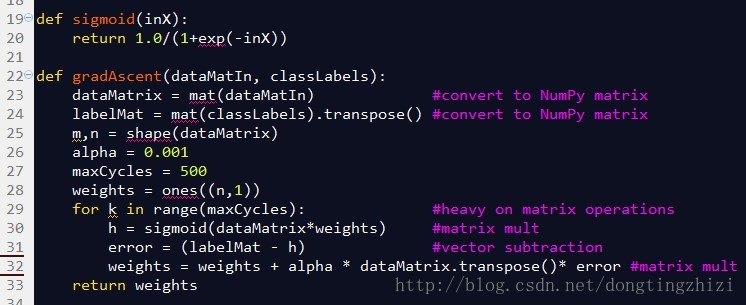
图4中是《机器学习实战》中给出的部分实现代码。
图4
sigmoid函数就是前文中的g(z)函数,参数inX可以是向量,因为程序中使用了Python的numpy。
gradAscent函数是梯度上升的实现函数,参数dataMatin和classLabels为训练数据,23和24行对训练数据做了处理,转换成numpy的矩阵类型,同时将横向量的classlabels转换成列向量labelMat,此时的dataMatrix和labelMat就是(18)式中的x和y。alpha为学习步长,maxCycles为迭代次数。weights为n维(等于x的列数)列向量,就是(19)式中的θ。
29行的for循环将更新θ的过程迭代maxCycles次,每循环一次更新一次。对比3.4节最后总结的向量化的θ更新步骤,30行相当于求了A=x.θ和g(A),31行相当于求了E=g(A)-y,32行相当于求θ:=θ-α.x'.E。所以这三行代码实际上与向量化的θ更新步骤是完全一致的。
正则化Regularization(还需更新,不透)
过拟合问题
对于线性回归或逻辑回归的损失函数构成的模型,可能会有些权重很大,有些权重很小,导致过拟合(就是过分拟合了训练数据),使得模型的复杂度提高,泛化能力较差(对未知数据的预测能力)。
下面左图即为欠拟合,中图为合适的拟合,右图为过拟合。

问题的主因
过拟合问题往往源自过多的特征。
解决方法
1)减少特征数量(减少特征会失去一些信息,即使特征选的很好)
- 可用人工选择要保留的特征;
- 模型选择算法;
2)正则化(特征较多时比较有效)
- 保留所有特征,但减少θ的大小
正则化方法
正则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项或惩罚项。正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化项就越大。
从房价预测问题开始,这次采用的是多项式回归。左图是适当拟合,右图是过拟合。

直观来看,如果我们想解决这个例子中的过拟合问题,最好能将 的影响消除,也就是让
的影响消除,也就是让 。假设我们对
。假设我们对 进行惩罚,并且令其很小,一个简单的办法就是给原有的Cost函数加上两个略大惩罚项,例如:
进行惩罚,并且令其很小,一个简单的办法就是给原有的Cost函数加上两个略大惩罚项,例如:

这样在最小化Cost函数的时候, 。
。
正则项可以取不同的形式,在回归问题中取平方损失,就是参数的L2范数,也可以取L1范数。取平方损失时,模型的损失函数变为:

lambda是正则项系数:
- 如果它的值很大,说明对模型的复杂度惩罚大,对拟合数据的损失惩罚小,这样它就不会过分拟合数据,在训练数据上的偏差较大,在未知数据上的方差较小,但是可能出现欠拟合的现象;
- 如果它的值很小,说明比较注重对训练数据的拟合,在训练数据上的偏差会小,但是可能会导致过拟合。
正则化后的梯度下降算法θ的更新变为:

正则化后的线性回归的Normal Equation的公式为:

其他优化算法
- Conjugate gradient method(共轭梯度法)
- Quasi-Newton method(拟牛顿法)
- BFGS method
- L-BFGS(Limited-memory BFGS)
后二者由拟牛顿法引申出来,与梯度下降算法相比,这些算法的优点是:
- 第一,不需要手动的选择步长;
- 第二,通常比梯度下降算法快;
但是缺点是更复杂。
参考
http://blog.csdn.net/dongtingzhizi/article/details/15962797
http://m.blog.csdn.net/article/details?id=51069254








 本文介绍了逻辑回归的原理和实现,包括构造h函数、Cost函数、J函数以及梯度下降法求解最佳参数。讨论了过拟合问题及其原因,并提出正则化作为解决方案,重点阐述了正则化项在Cost函数中的作用以及不同类型的正则化。最后提到了其他优化算法,如共轭梯度法和拟牛顿法。
本文介绍了逻辑回归的原理和实现,包括构造h函数、Cost函数、J函数以及梯度下降法求解最佳参数。讨论了过拟合问题及其原因,并提出正则化作为解决方案,重点阐述了正则化项在Cost函数中的作用以及不同类型的正则化。最后提到了其他优化算法,如共轭梯度法和拟牛顿法。


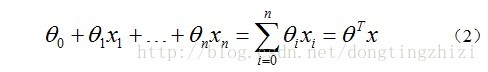
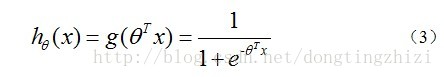
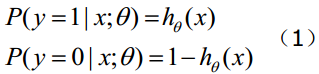
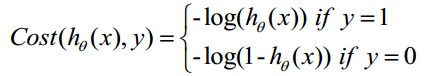
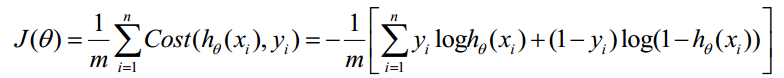
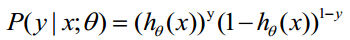
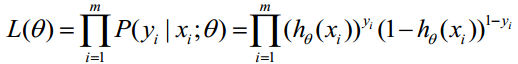
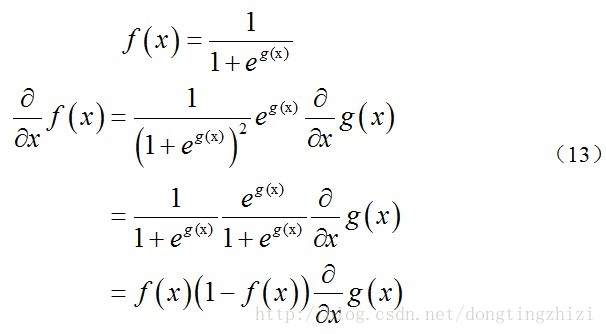
















 2059
2059

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








