Author: DivinerShi
最近在看相关东西,直接看文献的话,废话太多,中文的相关解释又很少,所以直接把wiki的翻译过来了,并做一点扩展。wiki英文原版
热核特征(Heat Kernel signature,HKS)是用于形变三维形状分析的特征描述子,属于谱形状分析方法。对于三维形状上的每个点,HKS定义了它的特征向量(feature vector)用于表示点的局部和全局属性。其广泛应用于是三维分割、分类、结构探索、形状匹配和形状检索。
HKS由Jian Sun,Maks Ovsjanikov 和Leonidas Guibas在2009年提出。它是基于热核(heat kernel)提出来的。HKS是基于拉普拉斯贝尔特米算子的形状描述子。
简单理解的话,热核特征是去计算三维模型表面的每个点,随时间变化后热量的剩余情况,因为每个点周围的情况是不一样的,这样的话,每个点假设都有一个相同的初始热量,随时间推移,因为点周边的情况不一样,那么热量扩散的速度也不一样,所以随着时间的变化,每个点的热量变化将会形成一条下降的曲线,再把这条曲线离散化,我们就可以得到一个点的热核特征。再按该方法去计算每个点的热核特征,我们就可以得到整个三维模型的热核特征,可以用一个大矩阵表示。
OverView
HKS具有等距变换不变性(简单的说就是在三维模型发生非拉伸形变,如铰链,关节等变换的时候具有不变性质的属性),所以广泛使用在非刚性三维形状处理任务上。对每个确定的关键点使用特征向量进行表示。
HKS是基于表面热扩散的概念产生的,给定一个表面初始热量分布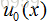
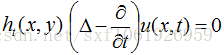
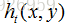
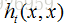
Technical details
黎曼流形M上的热扩散方法如下:
其中,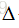
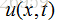
对热核进行特征分解得到:
其中,
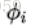
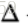
热核能完全等距的表征一个形状表面:对于任何两个黎曼流形M和N上的满映射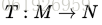
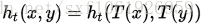
HKS和热核一样,在M和N的
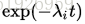
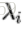
Practical considerations
一般来说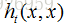
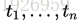

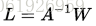
其中A是一个A(i,i)表示的正对角矩阵,它对应网格中共享顶点i的三角形面积,W是一个对称的半正定权重矩阵。L能被分解成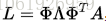
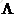
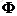
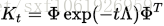
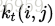
Limitations
1、不重复的特征值
使用HKS来表示模型表面的等距的主要属性需要保证模型表面的特征值不重复。也有一些特殊的例子不需要保证这个条件(尤其是有对称性质的),如球体。
2、时间参数选择
HKS中时间参数是和全局信息尺度非常相关的。但是没有很直接的方式去离散化的选择时间。现存的用对数的方式选择时间只是一个没有保证的启发式方法。
3、时间复杂度
离散热核需要大小为nxn的矩阵的特征分解,其中n是流形的网格表示(mesh)的顶点数。随着n的增加,计算特征分解的代价很高。但是需要指出的是,因为特征值的逆指数依赖,通常只需要很小的特征向量(少于100)就足够去获得一个HKS的很好的近似。
4、非等距变换
热核的性能保证只适用于等距变换。但是,真实形状常常不是等距变换的。一个简单的例子是当人握起拳头的时候,两个手指的测地距离发生了改变,就是两个手指挨在一起了。
Relation with other methods
1、曲率
点x的连续的HKS,黎曼流形上的
因此,HKS能解释为点x在尺度t时的曲率。
2、波核特征(Wave kernel signature,wks)
WKS和HKS相似,只是把热方程改成了薛定谔波动方程( Schrödinger wave equation):

其中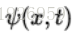
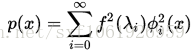
其中f是初始能量分布。通过固定一系列这些能量分布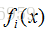
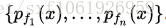
3、全局特征点(GPS)
和HKS相似,GPS是基于拉普拉斯贝尔特米算子。点x处的GPS是在点x用拉普拉斯贝尔特米算子的尺度特征函数计算出的向量。GPS是一个全局特征,而HKS的尺度是可以根据热扩散的时间参数不同而不同。因此,HKS能被用在局部形状匹配应用中,而GPS不行。
4、谱图小波特征(SGWS)
SGWS提供了谱描述子的一般形式,其中可以通过制定滤波函数来获得HKS。SGWS是一个多解的局部描述子。不仅等距不变而且更加简洁,易于计算,结合了带通和低通滤波器的优点。
Extensions
1、尺度不变
尽管HKS在多尺度表示形状,但是并不是天生的尺度不变。举例来说,对于一个形状和它的不同尺度版本的形状,在没有预先标准化的前提下,它们的HKS是不一样的。一个简单的方法是去报尺度不变性是去预先缩放形状到有一个相同的表面积。使用上面的符号,就是说:
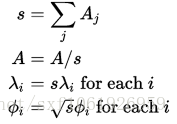
或者说,HKS的尺度不变版本也可以通过构造一个尺度空间来表示。在尺度空间中,一个缩放的形状的HKS对应到转化为一个乘法因子。该HKS的傅立叶变化将时间平移变换到复平面中,并且通过考虑变换的模量可以消除对平移的依赖性。(这块我也不懂,直译的)。
2、体积HKS
HKS被定义为3D形状的边界表面,表示为一个2D的黎曼流形。代替只考虑边界,3D形状的整个体积能被考虑定义HKS的体积版本。体积HKS定义和一般的HKS一样,通过考虑整个体积上(作为三个子流形)的热方程,并且在3D形状的2D流形边界上定义了一个Neumann边界条件。体积HKS表示了体积的等距变换,其表示的对真实的3D对象的变换比边界变换更真实。(这块也不是很懂,直译)。
3、性状搜素
尺度不变HKS特征可以被用在词袋模型中,用于形状检索。这个特征,通过考虑他们的一些空间关系,被用于构建几何单词,通过这种方法,一个特征能表示为一个word,一个形状表示为一个sentence。形状是通过二进制代码形成一个索引集合,给定一个查询形状,在索引中相似的形状可能是等距变换的,然后通过海明距离,找出距离最短的形状。
References
- Sun, J. and Ovsjanikov, M. and Guibas, L. (2009). “A Concise and Provably Informative Multi-Scale Signature-Based on Heat Diffusion”. Computer Graphics Forum. 28. pp. 1383–1392.
2.Alexander M. Bronstein (2011). “Spectral descriptors for deformable shapes”. arXiv:1110.5015
3.Grigor’yan, A. (2006). “Heat kernels on weighted manifolds and applications”. Contemporary Mathematics. 398: 93–191. doi:10.1090/conm/398/07486.
4.Aubry, M. and Schlickewei, U. and Cremers, D. (2011). “The Wave Kernel Signature—A Quantum Mechanical Approach to Shape Analysis”. IEEE International Conference on Computer Vision (ICCV) - Workshop on Dynamic Shape Capture and Analysis (4DMOD).
5.Rustamov, R.M. (2007). “Laplace–Beltrami eigenfunctions for deformation invariant shape representation”. Proceedings of the fifth Eurographics symposium on Geometry processing. Eurographics Association. pp. 225–233.
6.C. Li; A. Ben Hamza (2013). “A multiresolution descriptor for deformable 3D shape retrieval”. The Visual Computer: 513–524.
7.Bronstein, M.M.; Kokkinos, I. (2010). “Scale-invariant heat kernel signatures for non-rigid shape recognition”. Computer Vision and Pattern Recognition (CVPR), 2010. IEEE. pp. 1704–1711.
8.Raviv, D. and Bronstein, M.M. and Bronstein, A.M. and Kimmel, R. (2010). “Volumetric heat kernel signatures”. Proceedings of the ACM workshop on 3D object retrieval. ACM. pp. 30–44.
9.Bronstein, A.M. and Bronstein, M.M. and Guibas, L.J. and Ovsjanikov, M. (2011). “Shape google: Geometric words and expressions for invariant shape retrieval”. ACM Transactions on Graphics. ACM. 30 (1).
网上找了些都不能用,师兄给了个可运行的matlab代码,共享下。
热核特征的matlab可运行代码(github地址)








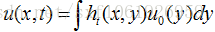
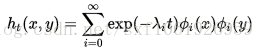
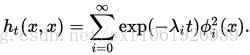
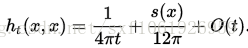
















 169
169

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








