范数的一般性质:
- 严格正定性:对任意矩阵
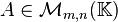 ,都有
,都有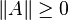 ,且等号成立当且仅当
,且等号成立当且仅当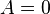 ;
; - 线性性:对任意系数
 、任意矩阵
、任意矩阵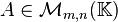 ,都有
,都有 ;
; - 三角不等式:任意矩阵
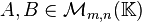 ,都有
,都有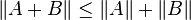 。则称之为
。则称之为 上的一个矩阵范数。
上的一个矩阵范数。
此外,某些定义在方块矩阵组成空间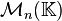 上的矩阵范数满足一个或多个以下与的条件:
上的矩阵范数满足一个或多个以下与的条件:
这里主要看下p-范数:
p-范数诱导的矩阵范数
当 和
和 中装备的向量范数都是
中装备的向量范数都是 -范数的时候,诱导的矩阵范数也称为矩阵的诱导
-范数的时候,诱导的矩阵范数也称为矩阵的诱导 -范数。具体来说就是:
-范数。具体来说就是:
在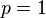 和
和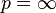 的情况下,其范数可以以下方式计算:
的情况下,其范数可以以下方式计算:
这些与矩阵的Schatten p-范数不同,也可以用 。来表示。
。来表示。
当p = 2(欧几里德范数)且m = n(方阵)时,诱导的矩阵范数就是谱范数。矩阵A的谱范数是A最大的奇异值或半正定矩阵A*A的最大特征值的平方根:
其中A*代表A的共轭转置。
任何诱导的矩阵范数都满足此不等式
其中ρ(A)是A的谱半径。事实上,可以证明ρ(A)是A的所有诱导范数的下界。
此外,我们有
-
 。
。
-
-
- 其实,一般用到的为最简单的形式:
-
若,那么

 当p取1,2,∞的时候分别是以下几种最简单的情形:1-范数:║x║1=│x 1│+│x 2│+…+│x n│2-范数:║x║2=(│x 1│ 2+│x 2│ 2+…+│x n│ 2) 1/2∞-范数:║x║∞=max(│x 1│,│x 2│,…,│x n│)
当p取1,2,∞的时候分别是以下几种最简单的情形:1-范数:║x║1=│x 1│+│x 2│+…+│x n│2-范数:║x║2=(│x 1│ 2+│x 2│ 2+…+│x n│ 2) 1/2∞-范数:║x║∞=max(│x 1│,│x 2│,…,│x n│)







 ;
; 。其中
。其中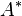 表示矩阵
表示矩阵 的
的
















 597
597

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








