8.12.15 ACM-ICPC数学 数论 威尔逊定理

8.12.15 ACM-ICPC数学 数论 威尔逊定理

威尔逊定理

威尔逊定理指出，对于素数 𝑝p，有：

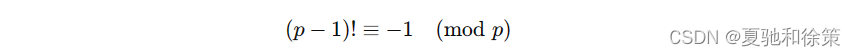
证明

我们可以利用同余方程或原根得到两种简洁的证明，此处略去不表。以下选择介绍前置知识较少的一种证明方法：

当 𝑝=2p=2 时，命题显然成立。

以下设 𝑝≥3p≥3，此时我们要证明 𝑍𝑝Zp​ 中所有非零元素的积为 −1‾−1​。

我们知道 𝑍𝑝Zp​ 中所有非零元素 𝑎a 都有逆元 𝑎−1a−1，于是 𝑍𝑝Zp​ 中彼此互逆的元素乘积为 1‾1。

但是要注意 𝑎a 和 𝑎−1a−1 可能相等。若 𝑎=𝑎−1a=a−1，则 𝑎2≡1(mod𝑝)a2≡1(modp)，即：

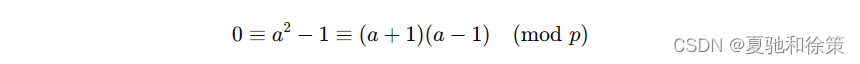
从而 𝑎≡1(mod𝑝)a≡1(modp) 或 𝑎≡−1(mod𝑝)a≡−1(modp)。

这说明 𝑍𝑝∖{0‾,1‾,−1‾}Zp​∖{0,1,−1​} 中所有元素的乘积为 1‾1，进而 𝑍𝑝Zp​ 中所有非零元素的积为 −1‾−1​。

应用

阶乘与素数

在某些情况下，有必要考虑以某个素数 𝑝p 为模的公式，包含分子和分母中的阶乘，就像在二项式系数公式中遇到的那样。只有当阶乘同时出现在分数的分子和分母中时，这个问题才有意义。否则，后续项 𝑝!p! 将减少为零。但在分数中，因子 𝑝p 可以抵消，结果将是非零。因此，要计算 𝑛! mod 𝑝n!modp，而不考虑阶乘中出现因数 𝑝p。

用 (𝑛!)𝑝(n!)p​ 表示这个修改的因子。例如：

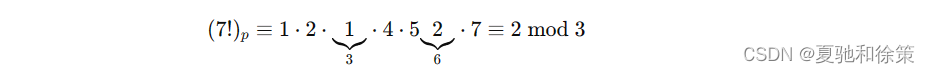
这种修正的阶乘可用于快速计算各种带取模和组合数的公式的值。

计算余数的算法

计算上述去掉因子 𝑝p 的阶乘模 𝑝p 的余数。

可以清楚地看到，除了最后一个块外，阶乘被划分为几个长度相同的块。

块的主要部分 (𝑝−1)!mod  𝑝(p−1)!modp 很容易计算，可以应用 Wilson 定理：

(𝑝−1)!≡−1(mod𝑝)(p−1)!≡−1(modp)

总共有 ⌊𝑛𝑝⌋⌊pn​⌋ 个块，因此需要将 ⌊𝑛𝑝⌋⌊pn​⌋ 写到 -1 的指数上。可以注意到结果在 -1 和 1 之间切换，因此只需要查看指数的奇偶性，如果是奇数，则乘以 -1。除了使用乘法，也可以从结果中减去 𝑝p。

最后一个部分块的值可以在 𝑂(𝑝)O(p) 的时间复杂度单独计算。

这只留下每个块的最后一个元素。如果隐藏已处理的元素，可以看到以下模式：

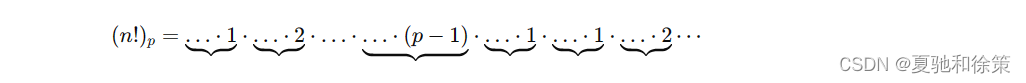
这也是一个修正的阶乘，只是维数小得多。它是：

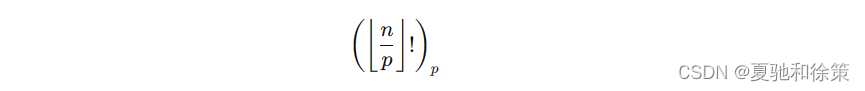
因此，在计算修改的阶乘 (𝑛!)𝑝(n!)p​ 中，执行了 𝑂(𝑝)O(p) 个操作，剩下的是计算 (⌊𝑛𝑝⌋!)𝑝(⌊pn​⌋!)p​，于是有了递归，递归深度为 𝑂(log⁡𝑝𝑛)O(logp​n)，因此算法的总时间复杂度为 𝑂(𝑝log⁡𝑝𝑛)O(plogp​n)。

如果预先计算阶乘 0!,1!,2!,…,(𝑝−1)!0!,1!,2!,…,(p−1)! 模 𝑝p，那么时间复杂度为 𝑂(log⁡𝑝𝑛)O(logp​n)。

Legendre公式

如果想计算二项式系数模 𝑝p，那么还需要考虑在 𝑛n 的阶乘的素因子分解中 𝑝p 出现的次数，或在计算修改因子时删除因子 𝑝p 的个数。

Legendre公式： 𝑛!n! 中含有的素数 𝑝p 的幂次 𝑣𝑝(𝑛!)vp​(n!) 为：

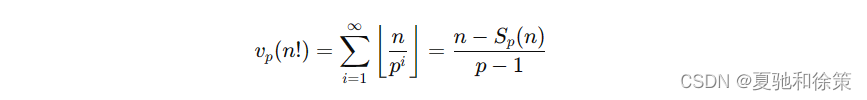
其中 𝑆𝑝(𝑛)Sp​(n) 为 𝑝p 进制下 𝑛n 的各个数位的和。

特别地，阶乘中 2 的幂次是 𝑣2(𝑛!)=𝑛−𝑆2(𝑛)v2​(n!)=n−S2​(n)。

实现

int factmod(int n, int p) {
  vector<int> f(p);
  f[0] = 1;
  for (int i = 1; i < p; i++) f[i] = f[i - 1] * i % p;
  int res = 1;
  while (n > 1) {
    if ((n / p) % 2) res = p - res;
    res = res * f[n % p] % p;
    n /= p;
  }
  return res;
}

Wilson 定理的推广

对于素数 𝑝p 和正整数 𝑞q 有：

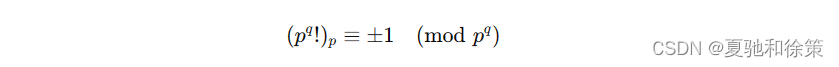
证明

依然考虑配对一个数与其逆元，也就是考虑关于 𝑚m 的同余方程 𝑚2≡1(mod𝑝𝑞)m2≡1(modpq) 的根的乘积，当 𝑝𝑞=2pq=2 时方程仅有一根，当 𝑝=2p=2 且 𝑞≥3q≥3 时有四根为 ±1,2𝑞−1±1±1,2q−1±1，其他时候则有两根为 ±1±1。

至此我们对 Wilson 定理的推广中的 ±1±1 有了详细的定义，即：

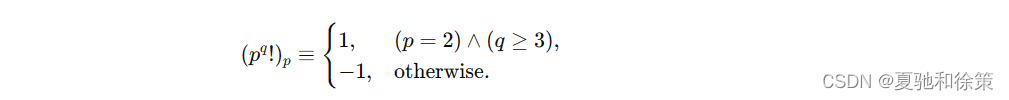
下文两个推论中的 ±1±1，均特指这样的定义：当模数 𝑝𝑞pq 取 8 及以上的 2 的幂时取 1，其余取 -1。

推论 1

对于素数 𝑝p、正整数 𝑞q、非负整数 𝑛n 和 𝑁0=𝑛 mod 𝑝𝑞N0​=nmodpq 有：

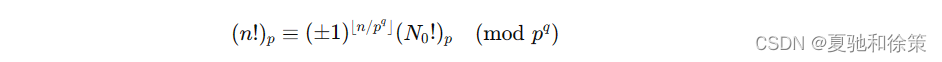
推论 2

对于素数 𝑝p 和正整数 𝑞q 和非负整数 𝑛n 有：

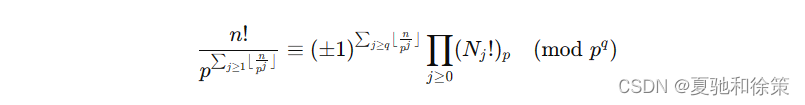
其中 𝑁𝑗=⌊𝑛/𝑝𝑗⌋ mod 𝑝𝑞Nj​=⌊n/pj⌋modpq 而 ±1±1 与上述相同。

例题

例题 HDU 2973 - YAPTCHA

给定 𝑛n，计算：

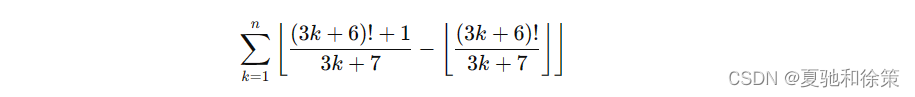
解题思路

参考代码

#include <iostream>

const int M = 1e6 + 5, N = 3 * M + 7;

bool not_prime[N];
int sum[M];

int main() {
  for (int i = 2; i < N; ++i)
    if (!not_prime[i])
      for (int j = 2; j * i < N; ++j) not_prime[j * i] = 1;
  for (int i = 1; i < M; ++i) sum[i] = sum[i - 1] + !not_prime[3 * i + 7];

  int t;
  std::cin >> t;
  while (t--) {
    int n;
    std::cin >> n;
    std::cout << sum[n] << std::endl;
  }
}