8.12.23 ACM-ICPC数学 数论 杜教筛

8.12.23 ACM-ICPC数学 数论 杜教筛

杜教筛简介

杜教筛用于处理一类数论函数的前缀和问题。对于数论函数 𝑓f，杜教筛可以在低于线性时间的复杂度内计算

算法思想

杜教筛的核心思想是构造一个 𝑆(𝑛)S(n) 关于 𝑆(⌊𝑛𝑖⌋)S(⌊in​⌋) 的递推式。

基本递推关系

对于任意一个数论函数 𝑔g，必满足：

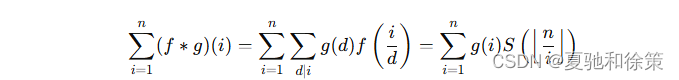
其中 𝑓∗𝑔f∗g 为数论函数 𝑓f 和 𝑔g 的狄利克雷卷积。

略证：𝑔(𝑑)𝑓(𝑖𝑑)g(d)f(di​) 就是对所有 𝑖≤𝑛i≤n 的贡献，因此变换枚举顺序，枚举 𝑑d， 𝑖𝑑di​。

于是有：

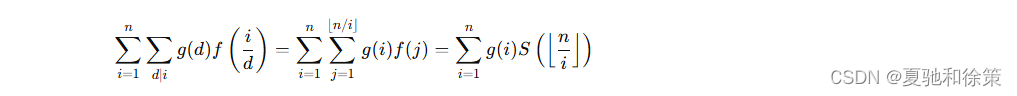
递推式推导

我们可以得到递推式：

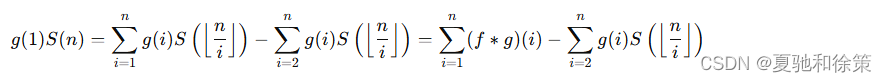
假如我们可以构造恰当的数论函数 𝑔g 使得：

1. 可以快速计算 ∑𝑖=1𝑛(𝑓∗𝑔)(𝑖)∑i=1n​(f∗g)(i)；
2. 可以快速计算 𝑔g 的前缀和，以用数论分块求解 ∑𝑖=2𝑛𝑔(𝑖)𝑆(⌊𝑛𝑖⌋)∑i=2n​g(i)S(⌊in​⌋)。

则我们可以在较短时间内求得 𝑔(1)𝑆(𝑛)g(1)S(n)。

注意事项

无论数论函数 𝑓f 是否为积性函数，只要可以构造出恰当的数论函数 𝑔g，便都可以考虑用杜教筛求 𝑓f 的前缀和。例如，考虑 𝑓(𝑛)=i𝜑(𝑛)f(n)=iφ(n)，显然 𝑓f 不是积性函数，但可取 𝑔(𝑛)=1g(n)=1，从而：

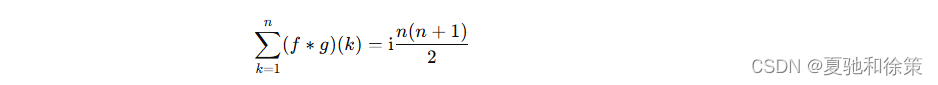
计算 ∑𝑘≤𝑚(𝑓∗𝑔)(𝑘)∑k≤m​(f∗g)(k) 和 ∑𝑘≤𝑚𝑔(𝑘)∑k≤m​g(k) 的时间复杂度均为 𝑂(1)O(1)，故可以考虑使用杜教筛。

时间复杂度

引理

对任意的 𝑚∈𝑅(𝑛)m∈R(n)，我们有 𝑅(𝑚)⊆𝑅(𝑛)R(m)⊆R(n)。

证明：令 𝑚=⌊𝑛𝑥⌋m=⌊xn​⌋，任取 ⌊𝑚𝑦⌋∈𝑅(𝑚)⌊ym​⌋∈R(m)，由整除分块/数论分块的引理1可知：

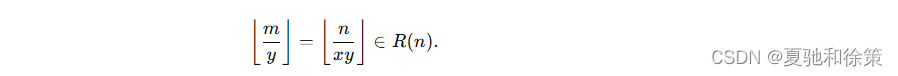
复杂度分析

设计算 ∑𝑖=1𝑛(𝑓∗𝑔)(𝑖)∑i=1n​(f∗g)(i) 和 ∑𝑖=1𝑛𝑔(𝑖)∑i=1n​g(i) 的时间复杂度均为 𝑂(1)O(1)。由引理可知：使用记忆化之后，每个 𝑆(𝑘)S(k) ( 𝑘∈𝑅(𝑛)k∈R(n) ) 均只会计算一次。

由整除分块/数论分块的引理2可知 ∣𝑅(𝑛)∣=2𝑛+Θ(1)∣R(n)∣=2n​+Θ(1)。设计算 𝑆(𝑛)S(n) 的时间复杂度为 𝑇(𝑛)T(n)，则：

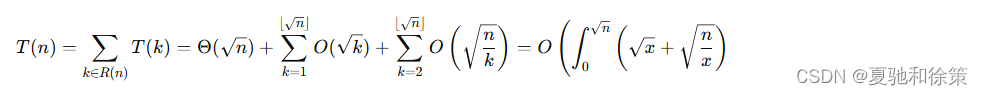
若我们可以预处理出一部分 𝑆(𝑘)S(k)，其中 𝑘=1,2,…,𝑚k=1,2,…,m，𝑚≥⌊𝑛⌋m≥⌊n​⌋。设预处理的时间复杂度为 𝑇0(𝑚)T0​(m)，则此时的 𝑇(𝑛)T(n) 为：

 

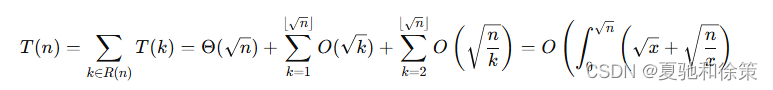
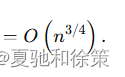
若 𝑇0(𝑚)=𝑂(𝑚)T0​(m)=O(m)（如线性筛），由均值不等式可知：当 𝑚=Θ(𝑛2/3)m=Θ(n2/3) 时，𝑇(𝑛)T(n) 取得最小值 𝑂(𝑛2/3)O(n2/3)。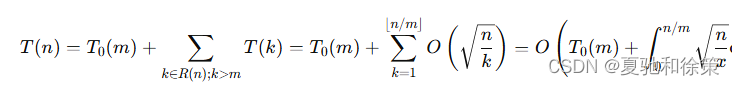

 

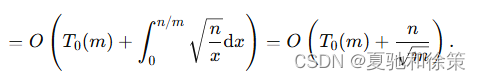
例题

问题一

P4213【模板】杜教筛（Sum）求 𝑆1(𝑛)=∑𝑖=1𝑛𝜇(𝑖)S1​(n)=∑i=1n​μ(i) 和 𝑆2(𝑛)=∑𝑖=1𝑛𝜑(𝑖)S2​(n)=∑i=1n​φ(i) 的值，1 \leq n < 2^{31}。

莫比乌斯函数前缀和

欧拉函数前缀和

我们知道：

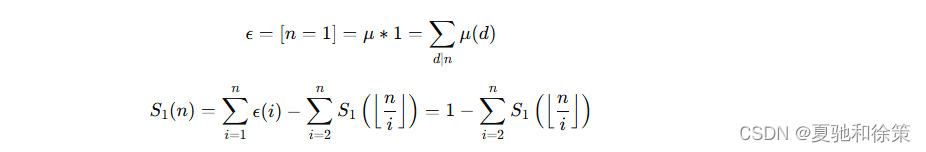
代码实现

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <map>
using namespace std;
const int maxn = 2000010;
long long T, n, pri[maxn], cur, mu[maxn], sum_mu[maxn];
bool vis[maxn];
map<long long, long long> mp_mu;

long long S_mu(long long x) {  // 求mu的前缀和
  if (x < maxn) return sum_mu[x];
  if (mp_mu[x]) return mp_mu[x];  // 如果map中已有该大小的mu值，则可直接返回
  long long ret = (long long)1;
  for (long long i = 2, j; i <= x; i = j + 1) {
    j = x / (x / i);
    ret -= S_mu(x / i) * (j - i + 1);
  }
  return mp_mu[x] = ret;  // 路径压缩，方便下次计算
}

long long S_phi(long long x) {  // 求phi的前缀和
  long long ret = (long long)0;
  long long j;
  for (long long i = 1; i <= x; i = j + 1) {
    j = x / (x / i);
    ret += (S_mu(j) - S_mu(i - 1)) * (x / i) * (x / i);
  }
  return (ret - 1) / 2 + 1;
}

int main() {
  scanf("%lld", &T);
  mu[1] = 1;
  for (int i = 2; i < maxn; i++) {  // 线性筛预处理mu数组
    if (!vis[i]) {
      pri[++cur] = i;
      mu[i] = -1;
    }
    for (int j = 1; j <= cur && i * pri[j] < maxn; j++) {
      vis[i * pri[j]] = true;
      if (i % pri[j])
        mu[i * pri[j]] = -mu[i];
      else {
        mu[i * pri[j]] = 0;
        break;
      }
    }
  }
  for (int i = 1; i < maxn; i++)
    sum_mu[i] = sum_mu[i - 1] + mu[i];  // 求mu数组前缀和
  while (T--) {
    scanf("%lld", &n);
    printf("%lld %lld\n", S_phi(n), S_mu(n));
  }
  return 0;
}

问题二

「LuoguP3768」简单的数学题

问题描述

求 ∑𝑖=1𝑛∑𝑗=1𝑛𝑖⋅𝑗⋅gcd⁡(𝑖,𝑗)(mod𝑝)∑i=1n​∑j=1n​i⋅j⋅gcd(i,j)(modp)，其中 𝑛≤1010n≤1010， 5×108≤𝑝≤1.1×1095×108≤p≤1.1×109， 𝑝p 是质数。

利用 𝜑∗1=id⁡φ∗1=id 做莫比乌斯反演化为：

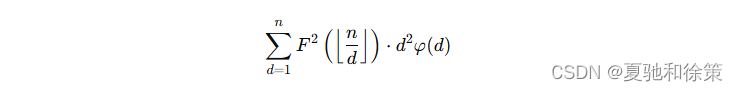
其中 𝐹(𝑛)=12𝑛(𝑛+1)F(n)=21​n(n+1)。

对 ∑𝑑=1𝑛𝐹(⌊𝑛𝑑⌋)2∑d=1n​F(⌊dn​⌋)2 做数论分块，𝑑2𝜑(𝑑)d2φ(d) 的前缀和用杜教筛处理。

代码实现

#include <cmath>
#include <cstdio>
#include <map>
using namespace std;
const int N = 5e6, NP = 5e6, SZ = N;
long long n, P, inv2, inv6, s[N];
int phi[N], p[NP], cnt, pn;
bool bp[N];
map<long long, long long> s_map;

long long ksm(long long a, long long m) {  // 求逆元用
  long long res = 1;
  while (m) {
    if (m & 1) res = res * a % P;
    a = a * a % P, m >>= 1;
  }
  return res;
}

void prime_work(int k) {  // 线性筛phi，s
  bp[0] = bp[1] = 1, phi[1] = 1;
  for (int i = 2; i <= k; i++) {
    if (!bp[i]) p[++cnt] = i, phi[i] = i - 1;
    for (int j = 1; j <= cnt && i * p[j] <= k; j++) {
      bp[i * p[j]] = 1;
      if (i % p[j] == 0) {
        phi[i * p[j]] = phi[i] * p[j];
        break;
      } else
        phi[i * p[j]] = phi[i] * phi[p[j]];
    }
  }
  for (int i = 1; i <= k; i++)
    s[i] = (1ll * i * i % P * phi[i] % P + s[i - 1]) % P;
}

long long s3(long long k) {  // 立方和
  return k %= P, (k * (k + 1) / 2) % P * ((k * (k + 1) / 2) % P) % P;
}

long long s2(long long k) {  // 平方和
  return k %= P, k * (k + 1) % P * (k * 2 + 1) % P * inv6 % P;
}

long long calc(long long k) {  // 计算S(k)
  if (k <= pn) return s[k];
  if (s_map[k]) return s_map[k];  // 对于超过pn的用map离散存储
  long long res = s3(k), pre = 1, cur;
  for (long long i = 2, j; i <= k; i = j + 1)
    j = k / (k / i), cur = s2(j),
    res = (res - calc(k / i) * (cur - pre) % P) % P, pre = cur;
  return s_map[k] = (res + P) % P;
}

long long solve() {
  long long res = 0, pre = 0, cur;
  for (long long i = 1, j; i <= n; i = j + 1) {
    j = n / (n / i);
    cur = calc(j);
    res = (res + (s3(n / i) * (cur - pre)) % P) % P;
    pre = cur;
  }
  return (res + P) % P;
}

int main() {
  scanf("%lld%lld", &P, &n);
  inv2 = k
sm(2, P - 2), inv6 = ksm(6, P - 2);
  pn = (long long)pow(n, 0.666667);  // n^(2/3)
  prime_work(pn);
  printf("%lld", solve());
  return 0;
}  // 不要为了省什么内存把数组开小,会卡80

参考资料

1. 任之洲，2016，《积性函数求和的几种方法》，2016年信息学奥林匹克中国国家队候选队员论文
2. 杜教筛的时空复杂度分析 - riteme.site

杜教筛作为处理数论函数前缀和问题的强大工具，其核心思想和复杂度分析让我们可以在相对较短的时间内解决看似复杂的问题。通过合适的数论函数 𝑔g 的选择和记忆化技术的应用，可以在高效计算的同时保证算法的可扩展性。