8.14.11 ACM-ICPC 组合数学 Entringer Number

、

8.14.11 ACM-ICPC 组合数学：Entringer Number

引言

在组合数学中，Entringer 数字（Entringer number）是一类特殊的数字序列，通常与斯特林数和排列问题有关。在这篇博客中，我们将深入探讨 Entringer 数字的定义、性质以及如何在 ACM-ICPC 编程竞赛中应用这些知识来解决相关问题。

Entringer 数字的定义

Entringer 数字 E(n,k)E(n, k)E(n,k) 是一种排列问题中的计数工具，用来表示从 nnn 个元素中选择 kkk 个元素的特定排列方式。具体来说，Entringer 数字的定义如下：

表示从 nnn 个元素中选择 kkk 个元素的所有排列方式，其中每个排列都是先递增后递减的。这种排列被称为摆动排列（zigzag permutation）或摆动序列（zigzag sequence）。

Entringer 数字的递归关系

Entringer 数字可以通过递归关系来计算。其递归关系如下：

初始条件为：

这一递归关系反映了在选择第 kkk 个元素时，有两种选择：要么选择当前序列的最后一个元素，要么选择剩余元素中的一个。

Entringer 数字的性质

1. 对称性：

2. 边界条件：

这些性质有助于简化计算和编程实现。

计算 Entringer 数字的算法

动态规划实现

为了有效地计算 Entringer 数字，我们可以采用动态规划的方法。以下是一个简单的动态规划实现：

#include <iostream>
#include <vector>

using namespace std;

// 计算 Entringer 数
int calculateEntringerNumber(int n, int k) {
    // 初始化动态规划表
    vector<vector<int>> dp(n + 1, vector<int>(n + 1, 0));

    // 边界条件
    for (int i = 1; i <= n; ++i) {
        dp[i][1] = dp[i][i] = 1;
    }

    // 递归关系
    for (int i = 2; i <= n; ++i) {
        for (int j = 2; j < i; ++j) {
            dp[i][j] = dp[i][j - 1] + dp[i - 1][i - j];
        }
    }

    return dp[n][k];
}

int main() {
    int n = 5;
    int k = 3;
    cout << "Entringer 数字 E(" << n << ", " << k << ") = " << calculateEntringerNumber(n, k) << endl;
    return 0;
}

示例解释

假设我们需要计算 E(5,3)E(5, 3)E(5,3)，使用上述算法：

1. 初始化动态规划表 dp，所有元素初始为 0。
2. 设置边界条件：dp[i][1] = dp[i][i] = 1。
3. 使用递归关系更新表格中的值。
4. 最后输出 dp[5][3] 的值。

Entringer 数字的应用

在 ACM-ICPC 以及其他编程竞赛中，Entringer 数字常用于解决与排列和计数相关的问题。例如，摆动排列的计数问题、特定序列生成问题等。理解和掌握 Entringer 数字的计算方法，可以大大提高我们在解决这些问题时的效率和准确性。

结论

Entringer 数字在组合数学中有着重要的地位，其递归关系和性质使得计算和应用变得相对简单。通过动态规划方法，我们可以高效地计算 Entringer 数字，并在各种编程竞赛中应用这些知识来解决复杂的排列和计数问题。希望这篇博客能帮助你更好地理解和应用 Entringer 数字，为你的竞赛准备增添一份力量。

---

引言

恩特林格数（Entringer number，OEIS A008281）是组合数学中的一个重要概念，特别是在排列和置换问题中。它们表示从 0 到 n 共 n+1 个数的置换数目，并且这种置换具有特定的模式。本文将详细介绍恩特林格数的定义、性质、递推关系及其在 ACM-ICPC 编程竞赛中的应用。

恩特林格数的定义

恩特林格数 E(n,k)E(n, k)E(n,k) 是满足下述条件的 0 到 n 共 n+1 个数的置换数目：

1. 首元素是 k；
2. 首元素的下一个元素比首元素小，再下一个元素比前一个元素大，再下一个元素比前一个元素小……后面相邻元素的大小关系均满足这样的规则。

初值

递推关系

Seidel–Entringer–Arnold 三角

恩特林格数可以排列成一个称为 Seidel–Entringer–Arnold 三角（OEIS A008280）的数字三角。这种排列方式按“牛耕”顺序（ox-plowing order）排列：

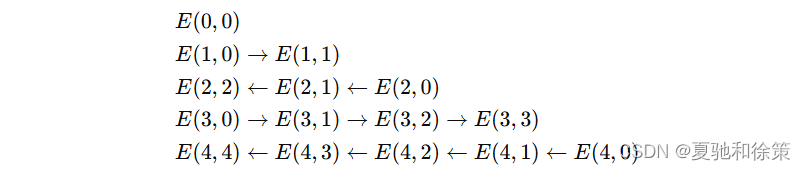
例如：

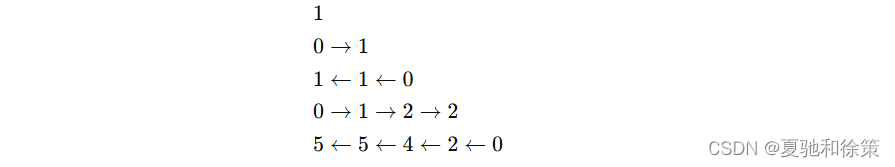
这种排列方式与其递推关系 E(n,k)=E(n,k−1)+E(n−1,n−k)E(n, k) = E(n, k-1) + E(n-1, n-k)E(n,k)=E(n,k−1)+E(n−1,n−k) 一致，便于记忆和理解。

恩特林格数的指数型生成函数

恩特林格数有一个指数型生成函数：

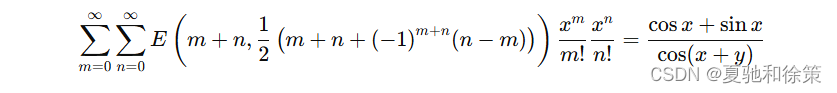
这个生成函数的系数分布实际上是 Seidel–Entringer–Arnold 三角的简单拉伸变形：

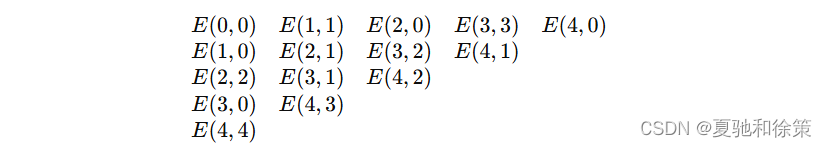
例如：

Zigzag 置换

一个 zigzag 置换（zigzag permutation）是一个 1 到 n 的排列 c1c_1c1​ 到 cic_ici​，使得任意一个元素 cic_ici​ 的大小都不介于 ci−1c_{i-1}ci−1​ 和 ci+1c_{i+1}ci+1​ 之间。

对于 zigzag 置换的个数 ZnZ_nZn​（OEIS A001250），从 n=0n=0n=0 开始有：

例如，前几个 nnn 的交替置换有：

Zigzag 数与 Entringer 数的关系

恩特林格数 E(n,k)E(n, k)E(n,k) 是首元素为 k 的 0 到 n 的交替置换个数。它们与 zigzag 数 ZnZ_nZn​ 有紧密的关系：

记 AnA_nAn​ 为 zigzag 数（Euler zigzag number，OEIS A000111），从 n=0n=0n=0 开始有：

递推关系

对于大于 1 的 n，zigzag 数满足递推关系：

当 n 为 0 时并不满足这个递推式，初值 A0A_0A0​ 和 A1A_1A1​ 都是 1。

生成函数

zigzag 数的生成函数可以表示为：

正切函数是奇函数，正割函数是偶函数，两者之和构成 zigzag 数的生成函数。

结论

恩特林格数在组合数学中扮演着重要角色，其递推关系和生成函数使得计算和应用变得相对简单。通过理解和掌握恩特林格数及其性质，可以在 ACM-ICPC 等编程竞赛中更好地解决复杂的排列和计数问题。希望这篇博客能帮助你更好地理解和应用恩特林格数，为你的竞赛准备增添一份力量。

参考资料与链接

• Entringer number - OEIS A008281
• Seidel–Entringer–Arnold triangle - OEIS A008280
• Euler zigzag number - OEIS A000111
• Wikipedia - Alternating permutation