现代通信原理4.3：白噪声

   作为遍历随机过程的一个例子，这部分我们来讨论白噪声。首先，我们来了解下信道噪声。

1、信道噪声简介

  所谓干扰（或噪声），是指有用信号以外一切不需要的信号及各种电磁干扰的总称。根据噪声(干扰)在信道中的表现形式，通常分为加性噪声(干扰)和乘性噪声(干扰)两类。乘性噪声(干扰)一般是一个复杂的函数，常常包括各种线性畸变、非线性畸变、交调畸变和衰落畸变等。加性噪声(干扰)则包括人为噪声、自然噪声和内部噪声等。顾名思义，加性噪声（干扰）是叠加在有用信号之上，而乘性噪声（干扰）则是与有用相乘。本课程主要讨论加性噪声。

1.1 加性噪声的不同来源

  根据来源的不同，噪声可分为自然噪声、人为噪声和内部噪声。

• 自然噪声
  自然噪声是指存在于自然界的各种电磁波，如闪电、雷暴及其它宇宙噪声。
• 人为噪声
  人为噪声来源于人类的各种活动，如电焊产生的电火花、车辆或各种机械设备运行时产生的电磁波和电源的波动，尤其是为某种目的而专门设置的干扰源(如电子对抗)。
• 内部噪声
  内部噪声指通信系统设备内部由元器件本身产生的热噪声、散弹噪声及电源噪声等。显然，只要通信电路使用导体、半导体等制成的器件，内部噪声就会存在。

1.2 信道噪声的不同表现形式

  根据信道噪声的表现形式，可分为单频噪声、脉冲噪声和起伏噪声。

• 单频噪声
  单频噪声是一种以某一固定频率出现的连续波噪声，它主要指无线电干扰，如50Hz的交流电噪声。频谱特性可能是单一频率，也可能是窄带谱。单频噪声的特点是一种连续波干扰。可以通过合理设计系统来避免单频噪声的干扰，例如用滤波器将工作频带之外的单频干扰滤除掉。
• 脉冲噪声
  脉冲噪声是一种随机出现的无规律噪声，它包括工业干扰中的电火花，断续电流以及天电干扰中的雷电等。脉冲噪声的特点是以突发脉冲形式出现、干扰持续时间短、脉冲幅度大、周期是随机的且相邻突发脉冲之间有较长的安静时间。由于脉冲很窄，所以其频谱很宽。但是随着频率的提高，频谱强度逐渐减弱。
• 起伏噪声
  起伏噪声主要是内部噪声，也包括来自空间的宇宙噪声。起伏噪声的特点是具有很宽的频带，并且始终存在，它是影响通信系统性能的主要因素。在以后各章分析通信系统抗噪声性能时，都是以起伏噪声为重点。

2、加性高斯白噪声(AWGN)信道模型

  从上面的介绍中我们知道，噪声在通信系统中是无处不在的。为了能够对通信系统进行分析，我们对加性噪声进行建模，模型如下图所示。

尽管在设计通信系统中，无论是发射机、接收机、还是信道，都会有噪声对信号产生干扰，但在分析模型中，我们认为加性噪声是在进入接收机之前，与信号进行叠加的。如上图所示，发射信号经过信道之后（这里的信道一般是指对信号的乘性干扰，例如无线通信系统中的衰落信道），即图中的$s(t)$，在进入接收机之前会叠加噪声$n(t)$，因此，进入接收机的信号为$r(t)=s(t)+n(t)$。下面，我们来看加性噪声$n(t)$的数学模型。

• 零均值高斯分布
    由于$n(t)$主要为起伏噪声，包括元器件本身产生的热噪声、散弹噪声等。这些噪声都可看成是无数独立的微小电流脉冲的叠加，根据中心极限定理，可以认为它们是服从高斯分布的，因此称这类噪声为高斯噪声，并且均值为0。
• 白噪声
    除了用概率分布描述噪声的特性外，还可用功率谱密度加以描述。若噪声的功率谱密度在整个频率范围内都是均匀分布的，即称其为白噪声。原因是其谱密度类似于光学中包含所有可见光光谱的白色光光谱。不是白色噪声的噪声称为带限噪声或有色噪声。具体来说，若随机信号$n(t)$，它的功率谱密度$P_N(f)$在所有频率上为一常数，则称$n(t)$为白噪声，即
  $$P_N(f)=\frac{n_0}{2},-\infty <f<\infty$$其中，$n_0$为正实常数，称为单边功率谱密度；$\frac{n_0}{2}$为$n(t)$的双边功率谱密度，其示意图如下图所示。显然，单边功率谱密度和双边功率谱密度不过是功率谱密度的不同表示形式而已，二者本质是相同的。
  
• 遍历（广义平稳）
    一般来说，认为噪声是遍历，因此显然它至少是广义平稳的。这样，我们就可以用$n(t)$上某时刻对应的随机变量$n$来描述它的特征.

  综上所述，我们通常认为，信道的加性噪声$n(t)$为遍历（广义平稳）、零均值、高斯分布的白噪声。我们把这样的信道称为加性高斯白噪声(Additive White Gaussian Noise, AWGN)信道。由于所有通信系统中都存在噪声，因而AWGN信道是最理想的信道。实际信道往往除了AWGN之外，还有各种衰减畸变等。
  对于加性高斯白噪声$n(t)$，其某个时刻的随机变量为$n$，则有$n\sim \mathcal{N}(0,{\sigma }_n^2)$，即$n$满足均值为0，方差为${\sigma }_n^2$的高斯分布。由于$n(t)$为遍历的，显然其直流分量为0，而平均功率为${\sigma }_n^2$。

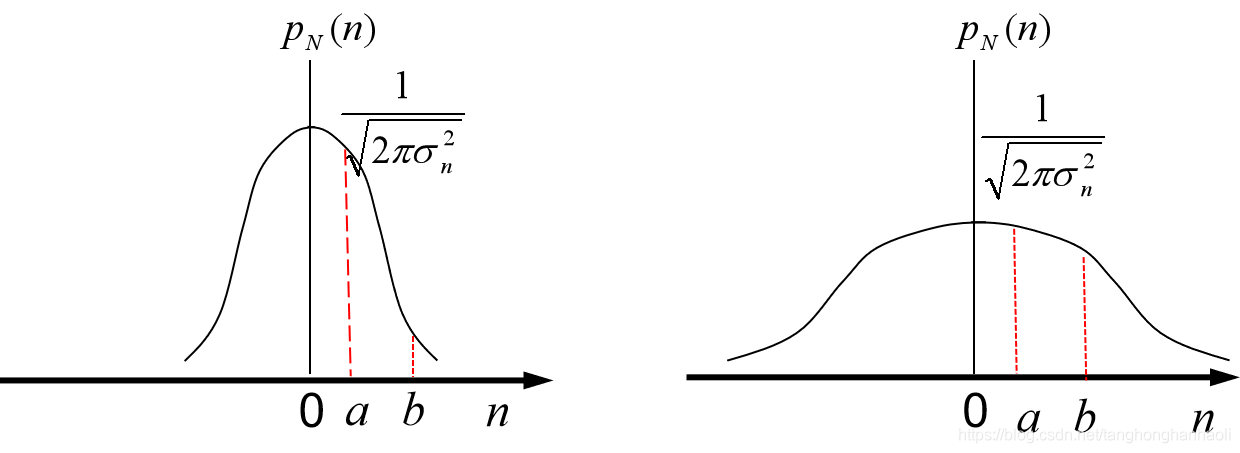
  若有两个高斯白噪声其概率密度函数如下图所示。请思考，这两张图，哪张图中的白噪声的功率更大呢？
  显然，应该是右边图中更大，因为$p_N(0)=\frac{1}{\sqrt{2\pi {\sigma }_n^2}}$，因此方差（功率）${\sigma }_n^2$越大，则图形看起来越矮胖（包围面积保持为1不变）。如图所示，对于偏离均值较少的数值$a$，当白噪声功率小的时候其概率大于噪声功率大的时候；但对于偏离均值较多的数值$b$，则大功率时出现概率更大。因此，零均值高斯白噪声功率越大，则出现较大值的概率也就越大。

  进一步，根据Wiener-Khintchine定理，我们知道AWGN的自相关函数和功率谱密度互为傅立叶变换，由于其功率谱密度为平坦的，即$P_N(f)=\frac{n_0}{2}$，因此有
$$R_N(\tau )={\mathcal{F}}^{-1}[P_N(f)]=\frac{n_0}{2}\delta (\tau )，$$这意味着，白噪声只有在$\tau =0$点是相关的，而在任何两个不相同时刻上的随机变量都是不相关的。

3、AWGN通过乘法器与滤波器

  《现代通信原理3.3：两个重要的信号处理模块-乘法器与滤波器》中，我们分析了确定信号通过乘法器和滤波器之后，信号波形与频谱密度发生的变化。这里我们给出随机信号与载波信号相乘，以及通过滤波器$h(t)$的情况，分别如下图(a)以及(b)所示。我们不对过程进行推导，仅仅将课程中会用到的结论加以呈现。

3.1 AWGN与载波信号相乘

  设$n(t)$为AWGN，其自相关函数与功率谱密度互为傅立叶变换，即
$$R_N(\tau )\leftrightarrow P_N(f).$$将$n(t)$与载波信号$c(t)=\cos 2\pi f_{c}t$，如上图(a)所示，即乘法器输出为$n_d(t)=n(t)\cos 2\pi f_{c}t$，其功率谱密度为
$$P_{N_d}(f)=\frac{1}{4}[\delta (f-f_c)+\delta (f+f_c)].$$回忆若确定信号$m(t)$与载波相乘，其频谱密度为
$$M(f)=\frac{1}{2}[M(f-f_c)+M(f+f_c)].$$二者相同之处是有频谱搬移，不同的是，功率谱密度系数为$\frac{1}{4}$而非$\frac{1}{2}$，可以理解为功率谱密度为功率量纲，因此是频谱密度（电压）的平方。

3.2 AWGN通过滤波器

  设$n(t)$为AWGN，其自相关函数与功率谱密度互为傅立叶变换，即
$$R_N(\tau )\leftrightarrow P_N(f).$$将$n(t)$通过冲激响应$h(t)$，频率传递函数为$H(f)$的滤波器，如上图(b)所示，即滤波器输出为$n_o(t)=n(t)\ast h(t)$，其功率谱密度为
$$P_{N_o}(f)=P_N(f)|H(f){|}^2,$$这里$|H(f){|}^2$称为功率传递函数。

【白噪声通过理想低通滤波器】
设理想低通滤波器频率传递函数为
$$H(f)=\{\begin{array}{rl}{K}_0{e}^{-j2\pi f{t}_d}& ,|f|\le f_m\\ 0& ,其它\end{array}$$则有功率传递函数为
$$|H(f){|}^2=\{\begin{array}{rl}{K}_0^2& ,|f|\le f_m\\ 0& ,其它\end{array}$$显然，可以得到滤波器输出噪声功率谱密度为
$$P_{N_o}(f)=P_N(f)|H(f){|}^2=\{\begin{array}{rl}\frac{n_0}{2}{K}_0^2& ,|f|\le f_m\\ 0& ,其它\end{array}$$由于$P_{N_o}(f)=\frac{n_0}{2}{K}_0^2\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{t}(\frac{f}{2f_m})$，可以得到$n_o(t)$的自相关函数为
$$R_{N_o}(\tau )=n_0{f}_m{K}_0^2\mathrm{S}\mathrm{a}(2\pi f_m\tau ).$$$n_o(t)$自相关函数与功率谱密度函数示意图如下图所示，被称为理想低通AWGN。其平均功率$P_{N_o}={\int }_{-\infty }^{\infty }{P}_N(f)df=n_0{K}_0^2{f}_m$。

【白噪声通过理想带通滤波器】
设理想带通滤波器频率传递函数为
$$H(f)=\{\begin{array}{rl}{K}_0{e}^{-j2\pi f{t}_d}& ,f_l\le |f|\le f_h\\ 0& ,其它\end{array}$$功率传递函数为
$$|H(f){|}^2=\{\begin{array}{rl}{K}_0^2& ,f_l\le |f|\le f_h\\ 0& ,其它\end{array}$$滤波器输出噪声功率谱密度为
$$P_{N_o}(f)=P_N(f)|H(f){|}^2=\{\begin{array}{rl}\frac{n_0}{2}{K}_0^2& ,f_l\le |f|\le f_h\\ 0& ,其它\end{array}$$此时，$n_o(t)$被称为理想带通AWGN，其功率谱密度如下图所示。可以得到平均功率为$P_{N_o}={\int }_{-\infty }^{\infty }{P}_N(f)df=n_0{K}_0^2(f_h-f_l)$。

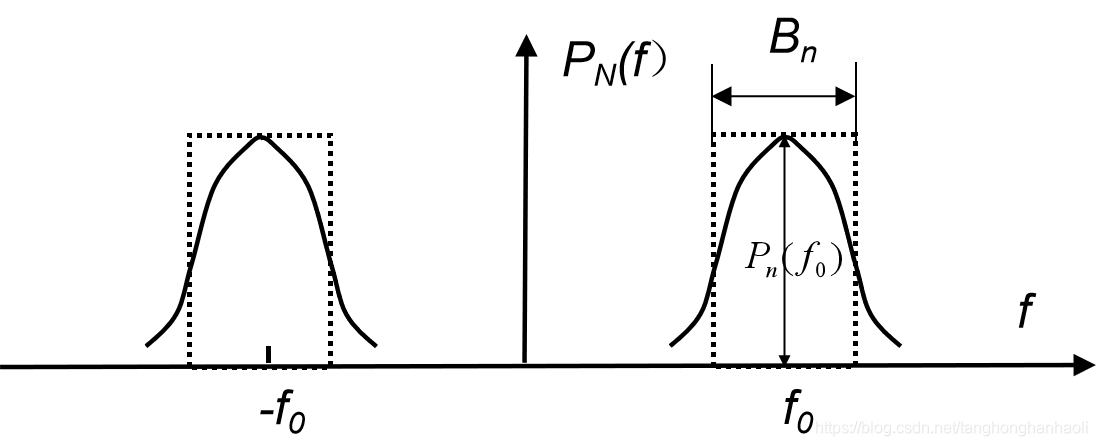
4、等效噪声带宽

  对于实际信号，由于其带宽是有限的，同时有较大从通带到阻带的过渡带，因而往往将其功率主要集中的频带的宽度定义为带宽，也因此有多种不同的定义方法，例如Sa函数的过零点带宽，以及3dB（即功率衰减为最大值的一半时）带宽等。这里我们定义等效噪声带宽$B_n$如下图所示，有
$$B_n=\frac{{\int }_{-\infty }^{\infty }{P}_N(f)df}{2P_N(f_0)}=\frac{{\int }_0^{\infty }{P}_N(f)df}{P_N(f_0)}.$$