估计理论(2)：Cramer-Rao下限

本文为《Steven M. Kay, Fundamentals of Statistical Signal Processing:Estimation Theory》一书的第3章。

  上一章我们谈到什么是最小方差无偏估计，即估计一方面是无偏的（估计值的均值为真值），同时又满足最小方差准则。这一章，我们讨论无偏估计方差的一种下限，即CRLB。

3.1 简介

  在实际中，如果能够为无偏估计的方差确定一个下限，将是非常有帮助的。在最好的情况下，如果该估计对于未知参数的所有取值都能达到下限。我们就可以据此推断这个估计是MVU估计。在最坏的情况下，它可以提供用来比较无偏估计性能的基准。进一步，它也提醒我们找到方差小于下限的无偏估计是不可能的，这在信号处理可用性研究中经常是有用的。
  尽管存在很多这样的方差限[1,2,3]，Cramer-Rao（CRLB）限要容易确定得多。此外，该定理让我们可以立即确定达到下限的估计是否存在。如果这样的估计不存在，也不会一无所获，因为我们可以找到近似达到下限的估计，正如第7章要介绍的。由于这些原因，这里我们主要讨论CRLB。

3.2 总结

  式(3.6)给出了标量参数的CRLB。如果式(3.7)条件满足，则下限可达，且很容易找到达到下限的估计。式(3.12)给出了确定CRLB的另外一种方法。对于WGN中具有一个未知参量的信号，式(3.14)给出了一种简便方法来计算下限。一般来说，即使存在$\theta$的有效估计，$\theta$某个函数的有效估计也不一定存在（除非函数是线性的）。用式(3.20)和(3.21)可以确定向量参数的CRLB。与标量情况相似，如果式(3.25)中条件满足，则下限可达，且很容易找到达到下限的估计。对于向量参数的函数，式(3.30)给出了其下限。式(3.31)给出了多维变量高斯PDF的Fisher信息矩阵（用来确定向量CRLB）的通用公式。最后，如果数据集来自WSS高斯随机过程，式(3.34)给出了依赖于PSD的近似CRLB。它是渐近有效的，或当数据记录长度变大时可用。

3.3 估计精度考虑

  在讨论CRLB定理之前，揭开哪些隐藏因素能够决定参数估计性能好坏，是值得的。由于我们所有的信息都是在观测数据及其PDF中具体表现的，因此估计精度取决于PDF一点也不奇怪。例如，如果PDF只与参数弱相关，甚至在极端情况下，完全无关，我们就没法期待估计是准确的。一般来说，PDF受未知参数的影响越大，我们的估计就越好。

观测数据的PDF，会影响观测精度。

---

【例3.1】依赖于未知参数的PDF
   如果观测到单个样本为
$$x[0]=A+w[0]$$其中$w[0]\sim \mathcal{N}(0,{\sigma }^2)$，并且想要估计$A$，我们预计如果${\sigma }^2$小的话，可以得到更好的估计。事实上，一个无偏估计是$\hat{A}=x[0]$。方差当然就是${\sigma }^2$，因此当${\sigma }^2$减小时，估计精度提升。看待这个问题的另外一个角度如图3.1所示，图中给出了两种不同方差时的PDF，即
$$p_i(x[0];A)=\frac{1}{\sqrt{2\pi {\sigma }_i^2}}\exp \left[-\frac{1}{2{\sigma }_i^2}(x[0]-A{)}^2\right]i=0,1\text{\hspace{1em}(3.1)}$$
在给定$x[0]$情况下，PDF与未知参数$A$的关系如图3.1所示。如果${\sigma }_1^2<{\sigma }_2^2$，则我们基于$p_1(x[0];A)$可以更准确地估计A。从图3.1我们可以理解这个结果。如果$x[0]=3$且${\sigma }_1=\frac{1}{3}$，则如图3.1(a)所示，出现$A>4$的可能性很小。为了看得更清楚，当$A$的值给定，我们确定$x[0]$落到区间$[x[0]-\delta /2,x[0]+\delta /2]=[3-\delta /2,3+\delta /2]$的概率为
$$\mathrm{P}\mathrm{r}\left\{3-\frac{\delta }{2}\le x[0]\le 3+\frac{\delta }{2}\right\}={\int }_{3-\frac{\delta }{2}}^{3+\frac{\delta }{2}}{p}_i(u;A)du$$当$\delta$取值很小时，有概率为$p_i(x[0]=3;A)\delta$。可以求得，$A$分别为3和4时，有$p_i(x[0]=3;A=3)\delta =1.20\delta$和$p_i(x[0]=3;A=4)\delta =0.01\delta$。显然当$A=4$时，$x[0]$落到3附近小区域的概率，与$A=3$时相对更小，因此可以不用考虑$A>4$的情况。可能有人会认为区间$3\pm 3{\sigma }_1=[2,4]$中A的值是可能的候选者。对于图3.1b中的PDF来说，它对于$A$的依赖性更弱，这里我们的可能候选区域就要宽的多，为$[0,6]$。

这个例子中，(b)中的方差更大，因而更发散，对均值的依赖性更弱，因此数据也就需要取得范围更大。如果也只有$[2,4]$区域中的数据，显然会有问题。

  如果把PDF看作未知参数的函数（其中$\mathbf{x}$是固定的），则其被称作似然函数。图3.1中给出了两个似然函数的例子。直观来看，似然函数的“尖锐程度”决定了我们能够在多大程度上精确估计未知参数。为了量化这个概念，我们观察到，可以用似然函数在其峰值处对数的二阶导数的负值，来有效测量锐度，即对数似然函数的曲率。在【例3.1】中，我们考虑PDF的自然对数为
$$\ln p(x[0];A)=-\ln \sqrt{2\pi {\sigma }^2}-\frac{1}{2{\sigma }^2}(x[0]-A{)}^2,$$因此一次导数为
$$\frac{\partial \ln p(x[0];A)}{\partial A}=\frac{1}{{\sigma }^2}(x[0]-A),\text{\hspace{1em}(3.2)}$$其二次导数的负值为
$$-\frac{{\partial }^2\ln p(x[0];A)}{\partial A^2}=\frac{1}{{\sigma }^2}.\text{\hspace{1em}(3.3)}$$随着${\sigma }^2$减小，曲率增大。由于我们已知估计$\hat{A}=x[0]$的方差为${\sigma }^2$，因此对于这个例子，有
$$\mathrm{v}\mathrm{a}\mathrm{r}(\hat{A})=\frac{1}{-\frac{{\partial }^2\ln p(x[0];A)}{\partial A^2}}\text{\hspace{1em}(3.4)}$$即曲率增加，方差减小。尽管在这个例子里，二次导数与$x[0]$无关，通常二次导数是与其相关的。因此，对于曲率更恰当的定义是
$$-\mathrm{E}\left[\frac{{\partial }^2\ln p(x[0];A)}{\partial A^2}\right],\text{\hspace{1em}(3.5)}$$用来表示对数似然函数的平均曲率。关于$p(x[0];A)$取期望，可以得到只与$A$有关的函数。期望说明了这样一个事实，依赖于$x[0]$的似然函数，本身是个随机变量。(3.5)的值越大，估计器的方差越小。

（测试数据）对数似然函数的曲率越大，则估计的方差越小。

3.4 Cramer-Rao下限

  下面我们先来看【定理3.1：标量参数的CRLB】，给出它的证明（附录3A），随后看几个例子。
【定理3.1：标量参数的CRLB】假设概率密度函数满足正则条件
$$\mathrm{E}\left[\frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }\right]=0，$$

例如，$x[n]=\theta +w[n]$，其中的$N$个样本 { x [ 1 ] , x [ 2 ] , … x [ N ] } \{x[1],x[2],\ldots x[N]\} {x[1],x[2],…x[N]}，构成观测数据向量$\mathbf{x}$，因此有概率密度函数为$p(\mathbf{x};\theta )$。上面式子中对$p(\mathbf{x};\theta )$求期望。

则任何无偏估计$\hat{\theta }$都满足
$$\mathrm{v}\mathrm{a}\mathrm{r}(\hat{\theta })\ge \frac{1}{-\mathrm{E}\left[\frac{{\partial }^2\ln p(\mathbf{x};\theta )}{\partial {\theta }^2}\right]}.\text{\hspace{1em}(3.6)}$$进一步，当且仅当
$$\frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }=I(\theta )[g(\mathbf{x})-\theta ],\text{\hspace{1em}(3.7)}$$有可能找到在所有$\theta$值上达到(3.6)的界的无偏估计，这里$g(\cdot )$和$I(\cdot )$为某个函数。此时，该估计$\hat{\theta }=g(\mathbf{x})$为MVU估计，最小方差为$1/I(\theta )$。

【例3.2】例3.1的CRLB。
  对于例3.1，从(3.3)和(3.6)，可以得到
$$\mathrm{v}\mathrm{a}\mathrm{r}(\hat{A})\ge {\sigma }^2,\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{A}$$

这里$x[0]=A+w[0]$，且$w[0]\sim \mathcal{N}(0,{\sigma }^2)$，无偏估计是$\hat{A}=x[0]$。

因此，即使对于单个的$A$的取值，也不存在方差小于${\sigma }^2$的无偏估计。然而事实上我们知道，如果$\hat{A}=x[0]$，那么对于所有的$A$，都有$\mathrm{v}\mathrm{a}\mathrm{r}(\hat{A})={\sigma }^2$。由于$x[0]$是无偏的且达到CRLB，因此它一定是MVU估计。Had we been unable to guess that $x[0]$ would be a good estimator, we could have used (3.7). 从(3.2)和(3.7)，如果我们令
$$\begin{array}{rl}\theta & =A\\ I(\theta )& =\frac{1}{{\sigma }^2}\\ g(x[0])& =x[0]\end{array}$$则(3.7)成立。因此$\hat{A}=g(x[0])=x[0]$为MVU估计。此外，注意到KaTeX parse error: Undefined control sequence: \I at position 29: …t A)=\sigma^2=1\̲I̲(\theta)，根据(3.6)，我们一定有
$$I(\theta )=-\mathrm{E}\left[\frac{{\partial }^2\ln p(\mathbf{x};\theta )}{\partial {\theta }^2}\right].$$下个例子之后我们再回来讨论这个问题。还可参见Problem 3.2，如何将其推广到非高斯的情况。

【例3.3】白高斯噪声中的直流电平
  将例3.1进行推广，考虑多观测量的情况
$$x[n]=A+w[n],n=0,1,\dots ,N-1$$其中$w[n]\sim \mathcal{N}(0,{\sigma }^2)$。为了决定$A$的CRLB，有
$$\begin{array}{rl}p(\mathbf{x};A)& =\prod _{n=0}^{N-1}\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left[-\frac{1}{2{\sigma }^2}(x[n]-A{)}^2\right]\\ & =\frac{1}{(2\pi {\sigma }^2{)}^{\frac{N}{2}}}\exp \left[-\frac{1}{2{\sigma }^2}\sum _{n=0}^{N-1}(x[n]-A{)}^2\right]\end{array}$$取一次导数，得到
$$\begin{array}{rl}\frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }& =\frac{\partial }{\partial A}\left[-\ln [(2\pi {\sigma }^2{)}^{\frac{N}{2}}]-\frac{1}{2{\sigma }^2}\sum _{n=0}^{N-1}(x[n]-A{)}^2\right]\\ & =\frac{1}{{\sigma }^2}\sum _{n=0}^{N-1}(x[n]-A)\\ & =\frac{N}{{\sigma }^2}(\bar{x}-A)\end{array}\text{\hspace{1em}(3.8)}$$这里的$\bar{x}$为$x$的样本平均。再求导，得到
$$\frac{{\partial }^2\ln p(\mathbf{x};A)}{\partial A^2}=-\frac{N}{{\sigma }^2}$$为常数，从(3.6)得到
$$\mathrm{v}\mathrm{a}\mathrm{r}(\hat{A})\ge \frac{{\sigma }^2}{N}\text{\hspace{1em}(3.9)}$$为CRLB。另外，通过比较(3.7)和(3.8)，我们可以看到样本平均估计达到CRLB界，因此一定是MVU估计。另外，最小方差再一次是由(3.8)中的常数$N/{\sigma }^2$的倒数得到的（这个例子的变形参见Problem 3.3-3.5）。
  下面我们证明，当达到CRLB时，有
$$\mathrm{v}\mathrm{a}\mathrm{r}(\hat{\theta })=\frac{1}{I(\theta )},$$其中，
$$I(\theta )=-\mathrm{E}\left[\frac{{\partial }^2\ln p(\mathbf{x};\theta )}{\partial {\theta }^2}\right].$$从(3.6)和(3.7)，可以得到
$$\mathrm{v}\mathrm{a}\mathrm{r}(\hat{\theta })=\frac{1}{-\mathrm{E}\left[\frac{{\partial }^2\ln p(\mathbf{x};\theta )}{\partial {\theta }^2}\right]}$$以及
$$\frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }=I(\theta )(\hat{\theta }-\theta ).$$对后者进行微分，可以得到
$$\frac{{\partial }^2\ln p(\mathbf{x};\theta )}{\partial {\theta }^2}=\frac{\partial I(\theta )}{\partial \theta }(\hat{\theta }-\theta )-I(\theta )$$对其求统计平均后取负值
$$-\mathrm{E}\left[\frac{{\partial }^2\ln p(\mathbf{x};\theta )}{\partial {\theta }^2}\right]=-\frac{\partial I(\theta )}{\partial \theta }[\mathrm{E}(\hat{\theta })-\theta ]-I(\theta )+I(\theta )=I(\theta )$$因此，可以得到
$$\mathrm{v}\mathrm{a}\mathrm{r}(\hat{\theta })=\frac{1}{I(\theta )},$$下面的例子中，我们可以看到CRLB并非总能达到。

【例3.4】相位估计
  现在我们对WGN中余弦信号的相位$\varphi$进行估计，即
$$x(n)=A\cos (2\pi f_{0}n+\varphi )+w[n]n=0,1,\dots ,N-1.$$这里假定幅度$A$和频率$f_0$已知，因此PDF为
$$\begin{array}{rl}p(\mathbf{x};\varphi )& =\frac{1}{(2\pi {\sigma }^2{)}^{\frac{N}{2}}}\exp \left[-\frac{1}{2{\sigma }^2}\sum _{n=0}^{N-1}(x[n]-A\cos (2\pi f_{0}n+\varphi ){)}^2\right]\end{array}$$对似然函数求微分，得到
$$\begin{array}{rl}\frac{\partial \ln p(\mathbf{x};\varphi )}{\partial \varphi }& =-\frac{1}{{\sigma }^2}\sum _{n=0}^{N-1}[x[n]-A\cos (2\pi f_{0}n+\varphi )]A\sin (2\pi f_{0}n+\varphi )\\ & =-\frac{A}{{\sigma }^2}\sum _{n=0}^{N-1}[x[n]\sin (2\pi f_{0}n+\varphi )-\frac{A}{2}\sin (4\pi f_{0}n+2\varphi )]\end{array}$$以及
$$\begin{array}{rl}\frac{{\partial }^2\ln p(\mathbf{x};\varphi )}{\partial {\varphi }^2}& =-\frac{A}{{\sigma }^2}\sum _{n=0}^{N-1}[x[n]\cos (2\pi f_{0}n+\varphi )-A\cos (4\pi f_{0}n+2\varphi )]\end{array}$$对其求统计平均并取负值，可以得到
$$\begin{array}{rl}-\mathrm{E}\left[\frac{{\partial }^2\ln p(\mathbf{x};\theta )}{\partial {\theta }^2}\right]& =\frac{A}{{\sigma }^2}\sum _{n=0}^{N-1}[A{\cos }^2(2\pi f_{0}n+\varphi )-A\cos (4\pi f_{0}n+2\varphi )]\\ & =\frac{A^2}{{\sigma }^2}\sum _{n=0}^{N-1}[\frac{1}{2}+\frac{1}{2}\cos (4\pi f_{0}n+2\varphi )-\cos (4\pi f_{0}n+2\varphi )]\\ & \approx \frac{N{A}^2}{2{\sigma }^2}\end{array}$$由于当$f_0$不接近等于0或者$1/2$（参见Problme 3.7），有
$$\frac{1}{N}\sum _{n=0}^{N-1}\cos (4\pi f_{0}n+2\varphi )\approx 0$$因此，可以得到
$$\mathrm{v}\mathrm{a}\mathrm{r}(\hat{\varphi })\ge \frac{2{\sigma }^2}{N{A}^2}.$$在这个例子中，让界成立的条件无法满足。因此，不存在能够达到CRLB的无偏相位估计。然而，仍然可能存在MVU估计，只是我们不知如何确定MVU估计是否存在，以及如果存在的话如何找到。第5章中的充分统计会帮助我们回答这些问题。

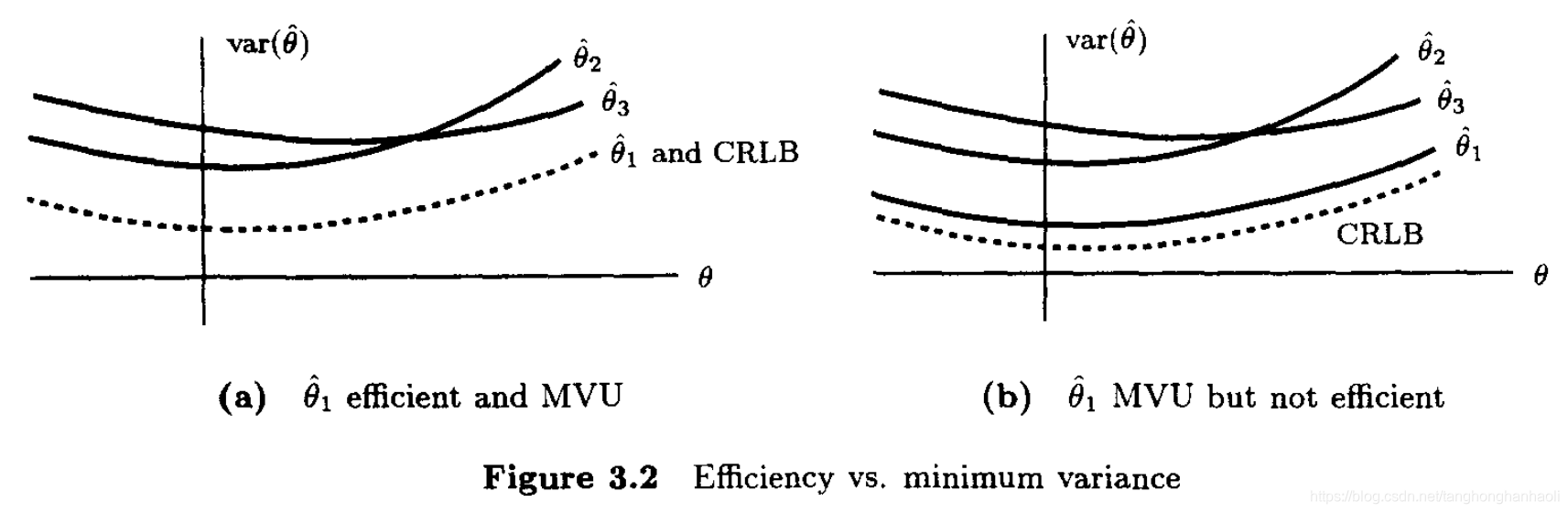
  如例3.3中的样本均值估计所示，一个无偏且达到CRLB的估计被认为是有效的，因为它有效地利用了数据。MUV估计可能是，也可能不是有效(efficient)的。例如，图3.2给出了所有可能估计的方差（为了方便说明，给出了三种无偏估计）。在图3.2a中，由于达到了CRLB，因此${\hat{\theta }}_1$是有效的，因此它也是MVU估计。然而，在图3.2b中，${\hat{\theta }}_1$没有达到CRLB，因此不是efficient。然而由于它的方差小于其它估计，因此依然是MVU。

  (3.6)给出的CRLB也可以用稍微有所不同的方式表达。尽管(3.6)用于评价更方便，另外一种表达在进行理论研究的时候更有用。根据下面等式（参见附录3A）
$$\mathrm{E}\left[{\left(\frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }\right)}^2\right]=-\mathrm{E}\left[\frac{{\partial }^2\ln p(\mathbf{x};\theta )}{\partial {\theta }^2}\right]，\text{\hspace{1em}(3.11)}$$因此
$$\mathrm{v}\mathrm{a}\mathrm{r}(\hat{\theta })\ge \frac{1}{\mathrm{E}\left[{\left(\frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }\right)}^2\right]}.\text{\hspace{1em}(3.12)}$$(参见问题3.8)。

3.5 WGN中信号的一般CRLB

3.6 参数的变换

3.7 扩展到矢量参数

3.8 矢量参数变换的CRLB

【附录3A】标量参数CRLB的推导

  对于标量参数$\alpha =g(\theta )$，其PDF由$\theta$参数化。我们考虑所有的无偏估计$\hat{\alpha }$，即
$$E(\hat{\alpha })=\alpha =g(\theta ),$$或
$$\int \hat{\alpha }p(\mathbf{x};\theta )d\mathbf{x}=g(\theta )\text{\hspace{1em}(3A.1)}$$在求导之前，我们先假定正定条件成立，即
$$\mathrm{E}\left[\frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }\right]=0，\text{\hspace{1em}(3A.2)}$$
注意到
$$\begin{array}{rl}\int \frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }p(\mathbf{x};\theta )d\mathbf{x}& =\int \frac{\partial p(\mathbf{x};\theta )}{\partial \theta }d\mathbf{x}\\ & =\frac{\partial }{\partial \theta }\int p(\mathbf{x};\theta )d\mathbf{x}\\ & =\frac{\partial 1}{\partial \theta }\\ & =0\end{array}$$因此，我们可以得出结论，如果微分和积分的顺序可以交换，那么正则条件就成立。通常情况下这是成立的，除非如Problem 3.1中，PDF的非零区域与未知有关参数有关。
  下面将(3A.1)的两边同时关于$\theta$取导，并交换偏导与积分的顺序，可以得到
$$\int \hat{\alpha }\frac{\partial p(\mathbf{x};\theta )}{\partial \theta }d\mathbf{x}=\frac{\partial g(\theta )}{\partial \theta }$$或者
$$\begin{array}{rl}\int \frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }p(\mathbf{x};\theta )d\mathbf{x}& =\int \frac{\partial p(\mathbf{x};\theta )}{\partial \theta }d\mathbf{x}\\ & =\frac{\partial }{\partial \theta }\int p(\mathbf{x};\theta )d\mathbf{x}\\ & =\frac{\partial 1}{\partial \theta }\\ & =0\end{array}$$因此，我们可得结论，如果微分和积分的顺序可以互换，则正则条件就能够满足。通常情况下都是如此，除非如Problem 3.1中，PDF的非零域与未知参数有关。
  下面把(3A.1)的等号两边都关于$\theta$求导，并交换偏导与积分的顺序，可以得到
$$\int \hat{\alpha }\frac{\partial p(\mathbf{x};\theta )}{\partial \theta }d\mathbf{x}=\frac{\partial g(\theta )}{\partial \theta }$$或者
$$\int \hat{\alpha }\frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }p(\mathbf{x};\theta )d\mathbf{x}=\frac{\partial g(\theta )}{\partial \theta }\text{\hspace{1em}(3A.3)}$$利用正则条件，由于
$$\int \alpha \frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }p(\mathbf{x};\theta )d\mathbf{x}=\alpha \mathrm{E}\left[\frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }\right]=0,$$则有
$$\int (\hat{\alpha }-\alpha )\frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }p(\mathbf{x};\theta )d\mathbf{x}=\frac{\partial g(\theta )}{\partial \theta }.\text{\hspace{1em}(3A.4)}$$下面我们利用Cauchy-Schwarz不等式
$${\left[\int w(x)g(x)h(x)dx\right]}^2\le \int w(x)g^2(x)dx\int w(x)h^2(x)dx,\text{\hspace{1em}(3A.5)}$$当且仅当$g(x)=ch(x)$的时候，上式中的等号成立，这里$c$为与$x$独立的常数，$g$和$h$为任意函数，而对于所有$x$，均有$w(x)\ge 0$。现在令
$$\begin{array}{rl}w(\mathbf{x})& =p(\mathbf{x};\theta )\\ g(\mathbf{x})& =\hat{\alpha }-\alpha \\ h(\mathbf{x})& =\frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }\end{array}$$并将柯西-施瓦茨不等式用于(3A.4)，可以得到
$${\left(\frac{\partial g(\theta )}{\partial \theta }\right)}^2\le \int (\hat{\alpha }-\alpha {)}^{2}p(\mathbf{x};\theta )d\mathbf{x}\int {\left(\frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }\right)}^{2}p(\mathbf{x};\theta )d\mathbf{x}$$或者
$$\mathrm{v}\mathrm{a}\mathrm{r}(\hat{\alpha })\ge \frac{{\left(\frac{\partial g(\theta )}{\partial \theta }\right)}^2}{\mathrm{E}\left[{\left(\frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }\right)}^2\right]}$$
注意到由于
$$\mathrm{E}\left[{\left(\frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }\right)}^2\right]=-\mathrm{E}\left[\frac{{\partial }^2\ln p(\mathbf{x};\theta )}{\partial {\theta }^2}\right]，$$

上式证明如下：
$$\begin{array}{rl}\int \frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }p(\mathbf{x};\theta )d\mathbf{x}& =0\\ \frac{\partial }{\partial \theta }\int \frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }p(\mathbf{x};\theta )d\mathbf{x}& =0\\ \int \left[\frac{{\partial }^2\ln p(\mathbf{x};\theta )}{\partial {\theta }^2}p(\mathbf{x};\theta )+\frac{\partial \ln p(\mathbf{x};\theta )}{\partial \theta }\frac{\partial p(\mathbf{x};\theta )}{\partial \theta }\right]d\mathbf{x}& =0\end{array}$$

因此有
$$\mathrm{v}\mathrm{a}\mathrm{r}(\hat{\alpha })\ge \frac{{\left(\frac{\partial g(\theta )}{\partial \theta }\right)}^2}{-\mathrm{E}\left[\frac{{\partial }^2\ln p(\mathbf{x};\theta )}{\partial {\theta }^2}\right]},$$此式为(3.16)。如果$\alpha =g(\theta )=\theta$，我们可以得到(3.6)。

---