脉冲整形原理

改变发射脉冲波形以适应信号传输

通常是通过限制传输的有效带宽。 通过这种方式对发射脉冲进行滤波，可以控制由信道引起的码间干扰。 在射频通信中，脉冲整形是必要的，使信号适合其频带。 典型的脉冲整形发生在行编码和调制之后。

https://zhuanlan.zhihu.com/p/106951888

https://blog.sciencenet.cn/blog-812827-1296408.html

使用有限脉冲响应滤波器的奈奎斯特脉冲整形

sinc 信号非常适合用于预防 ISI，但它不实用，因为它会在时间上无限延长。

阶数为 R 的有限脉冲响应 (FIR) 滤波器

为避免产生混叠，脉冲整形 FIR 滤波器必须至少按 q = 2 的系数进行过采样。换言之，在 TS 内必须至少有 1 个采样点。功率谱是由正弦脉冲的矩形频谱与矩形窗口的正弦形光谱的卷积产生。

（R. Schmogrow M. Winter，M. Meyer, D. Hillerkuss，S. Wolf, B. Baeuerle，A. Ludwig，B. Nebendahl， S. Ben-Ezra，J. Meyer，M. Dreschmann，M. Huebner，J. Becker，C. Koos，W. Freude 和 J. Leuthold ： 《超过 100 Gb/s 的实时奈奎斯特脉冲生成及其与 OFDM 的关系》，Optics Express，第 20 (1) 期， 第 317 – 337 页，2012 年 1 月)

第一行中，滤波器阶数为 16，信号跨越了 8 TS。在 FFT 中，可以看到有限时间窗口产生了失真。大部分功率位于奈奎斯特频段 (-0.5 FS 至 0.5 FS），但有一部分位于频段外。 功率谱以图谱形式显示谐波。

假设滤波器的长度增加一倍 (R = 32)，信号能够更好地适应带宽，但会出现振铃。

当 R = 1024 时，频谱几近完美；振铃仅在陡峭边沿上可见，功率谱还显示出较少的带外成分。

遗憾的是，滤波器的阶数 R 越高，滤波器设计的复杂程度也就越高。因此，通常希望采用满足要求的最低阶 R。

升余弦滤波器

为了获得更好的带外抑制和无振铃频谱，升余弦滤波器是合适的备选方案。脉冲响应取决于滚降因数α（0 至 1 之间的任意值）

升余弦滤波器也能满足奈奎斯特 ISI 准则，即，只有经采样的符号会对信号造成响应。 在采样点上的其他符号均为零。与 sinc 整形脉冲相比，升余弦信号要求更多的带宽。

归一化时域和频域呈现

在频率响应中，对于任何 α 值，曲线在 ±FS /2 的同一点上交叉，这是脉冲速率的一半。如前所述，这个是奈奎斯特频率——在不丢失信息的前提下进行数据传输所需的最小带宽。

当α = 1 时，几乎没有振铃，但频谱不会适应带宽。

当α = 0 时，情况正好相反：频率响应在带宽范围内为矩形（边沿上的过冲仅仅是数学效应，也称之为吉伯斯现象，没有任何实际影响）。然而，时域信号显示出更多振铃。

在采样点上，只有经过采样的符号会对信号造成响应，但为什么振铃会是问题？实际上， 当我们只在理想瞬间采样时，其他的符号均为零，因此振铃成为问题。在实际条件下，接收机几乎不可能在这个点上进行精确采样，因此在信号解读时始终会有部分 ISI 产生误差。

时域中的带宽限制和振铃抑制之间需要进行权衡。对于每一个光纤应用，在选择足够的 α 值时都要加以权衡。

实际的升余弦滤波器

不同滚降系数对最有希望的 400 Gbps 调制方案的影响：16-QAM。 图 4 显示了频域响应测量、眼图测量、以及对星座点之间转换产生的影响。

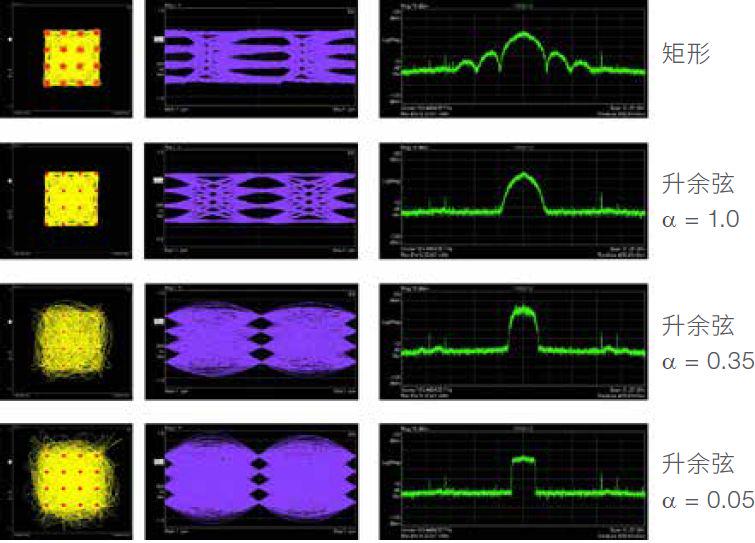
星座图、眼图和频谱

第一个图，无定形的矩形脉冲。已知只占据固定时间间隔的信号具有无限扩展的频谱； 在频率响应中可以看到大的旁瓣。眼图显示了开眼的宽带信号的典型特性。在星座点之间存在直接转换。

α = 1 的升余弦滤波器，频谱会变狭窄 ；不会再看到旁瓣。在眼图中，眼图张开度很大。星座点较小。这是带宽较窄的系统的典型特征。接收机端的检测带宽也会降低，由此减少了噪声。

α = 0.35 时，频宽进一步减少，星座点的大小也随之降低。星座点的转换开始显示很多过冲。这是因为当带宽降低时，符号间的跳变时间就会延长，体现在星座图中就是星座点之间存在很长的跳变曲线。眼图闭合，采样时间变得更加重要。

α = 0.05 时可以得到几近完美的矩形频谱。星座点之间的跳变显示了较大的过冲。完全闭合的眼图表明，采样点必须经过精确调整，以免产生误差。