Understanding SVM

最新推荐文章于 2024-07-20 22:56:53 发布

tcj2015

最新推荐文章于 2024-07-20 22:56:53 发布

阅读量245

点赞数

分类专栏： opencv 文章标签： opencv python

opencv 专栏收录该内容

7 篇文章 0 订阅

订阅专栏

1，Linearly Separable Data 线性数据切分

考虑下面这张图，有红色数据和蓝色数据。在KNN 中，作为测试数据，要测量所有的训练数据的距离并取最小距离值。这要消耗大量的时间来计算距离和大量的内存来保存训练数据。考虑这些数据都是图像提供的，我们是否正的需要那么多？

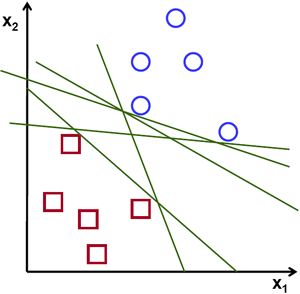
有另一种想法，找到一条线，f(x)= ax+by+c，把所有的数据分成两部分。当我们测试数据 X 来取代它，如果 f(X)>0 则在蓝色组，否则在红色组。我们叫这条线为决定边界（Decision Boundary）。这非常高效与节省内存。这样可以被直线分为两部分的数据，我们叫做线性可分（Linear Separable）。

下面的这张图，可以看到有许多这样的线。那一条才是我们要的？很直观，我们可以说里所有数据最远的那条就是我们要的。why？因为我们会被传入的数据干扰。数据不能影响分类精度。所以取最远的线有更强的抗干扰。SVM要做的事情就是找到这条离所有训练样本最大最小距离的直线。下图中的粗线通过图形的中间。

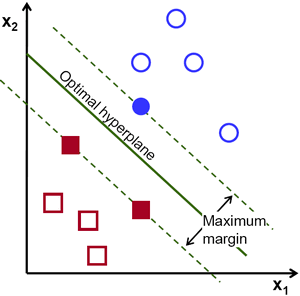
查找决定边界（Decision Boundary）需要所有的训练数据，需要么？当然不需要，只要靠近相反组的数据就够了。在本图中，有1个蓝色圆圈和两个红色方框，把它们叫做支持向量（Support Vectors），把通过他们所有的直线叫做支持平面（Support Planes），通过他们就足以找到决定边界，不用关系所有的数据，这样数据量减少了。

发生了什么，首先找到两个最能代表数据的超平面，比如蓝色数据的代表 $w^Tx+b_0 > 1$ ，而红色数据的代表 $w^Tx+b_0 < -1$ ，其中w是权重， $w=[w_1, w_2,..., w_n]$ ，x是特征向量 $x = [x_1,x_2,..., x_n]$ ，b0是偏移量。权重向量决定了决定边界的方向，偏移决定了位置。现在边界被定义在超平面的中间，所以表达式是 $w^Tx+b_0 = 0$ 。这到支持向量的最短距离就可以确定了， $distance_{support \, vectors}=\frac{1}{||w||}$ 。边缘是距离的两倍，我们要最大化这个边缘。比如我们得到一个新的函数L（w，b0）的一些约束，可以表示为：

$\min_{w, b_0} L(w, b_0) = \frac{1}{2}||w||^2 \; \text{subject to} \; t_i(w^Tx+b_0) \geq 1 \; \forall i$

ti是每一个分类， $t_i \in [-1,1]$ .

2，Non-Linearly Separable Data。分线性分割数据。

有些数据是无法用一条直线分为两半。比如一维数据 -3<X<3, -1<Q<1,很明显，这是无法线性分割的。单有一些方法可以解决这类问题，我们可以映射数据集到一个函数上F(x)=X^2。得到X在9，Q在1，这样就线性可分了。

另外我们将一位数据转为二维数据，可以使用F(x，x^2)来映射这些数据。X 变成（3,9）和（-3,9），Q是（-1,1）和（1,1），这样就线性可分了。总之，在低维非线性可分可以增加维数变为线性可分。

通常，将d维空间上的点映射到D维空间（D>d）来改变线性可分。有个概念可以帮我实现低维空间里计算高维空间里的点运算。

可以用下面的例子来说明

2维空间里面的两点， $p=(p_1,p_2)$ 和 $q=(q_1,q_2)$ ， $\phi$ 是可以将二维空间的点映射到三维空间的映射函数，

$\phi (p) = (p_{1}^2,p_{2}^2,\sqrt{2} p_1 p_2)\phi (q) = (q_{1}^2,q_{2}^2,\sqrt{2} q_1 q_2)$

定义一个核函数 $K(p,q)$ ，可以在为二维空间执行两点间的点运算

$K(p,q) = \phi(p).\phi(q) &= \phi(p)^T , \phi(q) \\ &= (p_{1}^2,p_{2}^2,\sqrt{2} p_1 p_2).(q_{1}^2,q_{2}^2,\sqrt{2} q_1 q_2) \\ &= p_{1}^2 q_{1}^2 + p_{2}^2 q_{2}^2 + 2 p_1 q_1 p_2 q_2 \\ &= (p_1 q_1 + p_2 q_2)^2 \\ \phi(p).\phi(q) &= (p.q)^2$

这就是说，一个三维空间的点运算可以用二维空间里点运算的平方来实现。

这也可以应用在高维空间。我们可以从低位空间计算自身在高维空间的特征。

出了这些概念，还有一些分类的问题。所以找到最大边缘的边界是不够的。我们同样要考虑分类的错误，有时,它可能会找到一个边缘较小的边界,来减少了误分类。无论如何我们需要修正一下，我们需要最大边缘的边界也需要最小边缘的边界，最小化标准：

$min \; ||w||^2 + C(distance \; of \; misclassified \; samples \; to \; their \; correct \; regions)$

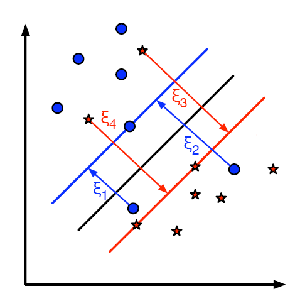
下面的图显示这个概念：

每个训练数据的样本定义为参数 $\xi_i$ ，是训练样本到‘决定地区’的距离。还没有分类的的数据在自己相应的超平面上，所以他们的距离是0.

所以优化问题为：

$\min_{w, b_{0}} L(w,b_0) = ||w||^{2} + C \sum_{i} {\xi_{i}} \text{ subject to } y_{i}(w^{T} x_{i} + b_{0}) \geq 1 - \xi_{i} \text{ and } \xi_{i} \geq 0 \text{ } \forall i$

如何选择参数C，很明显，这个问题的答案依赖于训练数据是如何分布的。

尽管没有一个常规答案，但是有利于我们总结一下规则：

1，大数值C提供的方案是提供最小边缘可以减少分类错误。这样产生错误分类就费劲了（不容易产生分类错误），优化后的目标需要较少的参数，分类错误是不允许的。

2，小数值C的方案是使用大只的边缘和较多的分类错误，这情况最小是不会考虑的很多组数量，这需要用大值边缘找到更多的超平面。

tcj2015

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
Understanding SVM

1，Linearly Separable Data 线性数据切分考虑下面这张图，有红色数据和蓝色数据。在KNN 中，作为测试数据，要测量所有的训练数据的距离并取最小距离值。这要消耗大量的时间来计算距离和大量的内存来保存训练数据。考虑这些数据都是图像提供的，我们是否正的需要那么多？有另一种想法，找到一条线，f(x)= ax+by+c，把所有的数据分成两部分。当我们
复制链接

扫一扫