1 二分查找算法(非递归)
1.1 二分查找算法(非递归)介绍:
1)前面我们讲过了二分查找算法,是使用递归的方式,下面我们讲解二分查找算法的非递归方式
2)二分查找法只适用于从有序的数列中进行查找(比如数字和字母等),将数列排序后再进行查找
3)二分查找法的运行时间为对数时间O(㏒₂n) ,即查找到需要的目标位置最多只需要㏒₂n步,假设从[0,99]的队列(100个数,即n=100)中寻到目标数30,则需要查找步数为㏒₂100 , 即最多需要查找7次( 2^6 < 100 < 2^7)
1.2 二分查找算法(非递归)代码实现
数组 {1,3, 8, 10, 11, 67, 100}, 编程实现二分查找, 要求使用非递归的方式完成.
代买实现:
/**
* @author Wnlife
* @create 2020-02-01 19:13
* <p>
* 二分查找算法,非递归的形式
*/
public class BinarySearchNoRecur {
public static void main(String[] args) {
int[] arr = {1, 3, 8, 10, 11, 67, 100};
int index = binarySearchNoRecur(arr, 100);
System.out.println("index=" + index);
}
public static int binarySearchNoRecur(int[] arr, int target) {
int first = 0;
int end = arr.length - 1;
while (first <= end) {
int mid = (first + end) >> 1;
if (arr[mid] > target) {
end = mid - 1;
} else if (arr[mid] < target) {
first = mid + 1;
} else {
return mid;
}
}
return -1;
}
}
2 分治算法
2.1 分治算法介绍
- 分治法是一种很重要的算法。字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础,如排序算法(快速排序,归并排序),傅立叶变换(快速傅立叶变换)……
- 分治算法可以求解的一些经典问题
- 二分搜索
- 大整数乘法
- 棋盘覆盖
- 合并排序
- 快速排序
- 线性时间选择
- 最接近点对问题
- 循环赛日程表
- 汉诺塔
2.2 分治算法的基本步骤
- 分治法在每一层递归上都有三个步骤:
- 分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题
- 解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题
- 合并:将各个子问题的解合并为原问题的解。
2.3 分治(Divide-and-Conquer§)算法设计模式如下
if |P|≤n0
then return(ADHOC(P))
//将P分解为较小的子问题 P1 ,P2 ,…,Pk
for i←1 to k
do yi ← Divide-and-Conquer(Pi) 递归解决Pi
T ← MERGE(y1,y2,…,yk) 合并子问题
return(T)
其中|P|表示问题P的规模;n0为一阈值,表示当问题P的规模不超过n0时,问题已容易直接解出,不必再继续分解。ADHOC§是该分治法中的基本子算法,用于直接解小规模的问题P。因此,当P的规模不超过n0时直接用算法ADHOC§求解。算法MERGE(y1,y2,…,yk)是该分治法中的合并子算法,用于将P的子问题P1 ,P2 ,…,Pk的相应的解y1,y2,…,yk合并为P的解。
2.4 分治算法最佳实践-汉诺塔

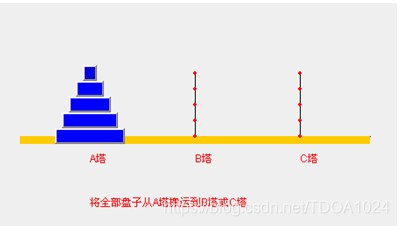
- 汉诺塔游戏的演示和思路分析:
1)如果是有一个盘, A->C
如果我们有 n >= 2 情况,我们总是可以看做是两个盘 1.最下边的盘 2. 上面的盘。
1)先把 最上面的盘 A->B
2)把最下边的盘 A->C
3)把B塔的所有盘 从 B->C
- 代码演示
/**
* @author Wnlife
* @create 2020-02-01 20:06
* <p>
* 分治算法实例:汉诺塔问题
*/
public class Hanoitower {
public static int count=0;
public static void main(String[] args) {
hanoiTower(5,'A','B','C');
System.out.println("一共需要移动"+count+"次");
}
public static void hanoiTower(int num, char a, char b, char c) {
count++;
//如果只有一个盘
if (num == 1) {
System.out.println("第1个盘从 " + a + "->" + c);
} else {
//如果有多个盘,将多个盘分为两部分:1.最底下的盘;2.上面的盘
//1.先把 最上面的所有盘 A->B, 移动过程会使用到 c
hanoiTower(num - 1, a, c, b);
//2.把最下边的盘 A->C
System.out.println("第" + num + "个盘从 " + a + "->" + c);
//3.把B塔的所有盘 从 B->C , 移动过程使用到 a塔
hanoiTower(num - 1, b, a, c);
}
}
}
3 动态规划算法
3.1 动态规划算法介绍
-
动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为小问题进行解决,从而一步步获取最优解的处理算法
-
动态规划算法与分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
-
与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。 ( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解 )
-
动态规划可以通过填表的方式来逐步推进,得到最优解.
3.2 动态规划算法最佳实践-背包问题
背包问题:有一个背包,容量为4磅 , 现有如下物品:
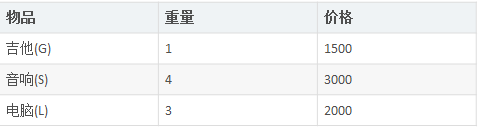
1)要求达到的目标为装入的背包的总价值最大,并且重量不超出;
2)要求装入的物品不能重复;
3)思路分析和图解
- 背包问题主要是指一个给定容量的背包、若干具有一定价值和重量的物品,如何选择物品放入背包使物品的价值最大。其中又分01背包和完全背包(完全背包指的是:每种物品都有无限件可用)
- 这里的问题属于01背包,即每个物品最多放一个。而无限背包可以转化为01背包。
- 算法的主要思想,利用动态规划来解决。每次遍历到的第i个物品,根据w[i]和v[i]来确定是否需要将该物品放入背包中。即对于给定的n个物品,设v[i]、w[i]分别为第i个物品的价值和重量,C为背包的容量。再令v[i][j]表示在前i个物品中能够装入容量为j的背包中的最大价值。则我们有下面的结果:
(1) v[i][0]=v[0][j]=0; //表示 填入表 第一行和第一列是0
(2) 当w[i]> j 时:v[i][j]=v[i-1][j] // 当准备加入新增的商品的容量大于 当前背包的容量时,就直接使用上一个单元格的装入策略
(3) 当j>=w[i]时: v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]}
// 当 准备加入的新增的商品的容量小于等于当前背包的容量,
// 装入的方式:
v[i-1][j]: 就是上一个单元格的装入的最大值
v[i] : 表示当前商品的价值
v[i-1][j-w[i]] : 装入i-1商品,到剩余空间j-w[i]的最大值
当j>=w[i]时: v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]} :
4)背包的填表过程
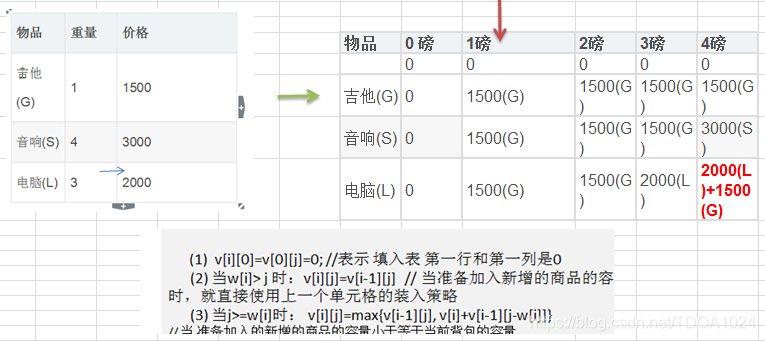
5)代码演示
/**
* @author Wnlife
* @create 2020-02-01 22:27
*
* 动态规划实例:背包问题
*/
public class KnapsackProblem {
public static void main(String[] args) {
//商品的重量
int[]w={1, 4, 3};
//商品的价值
int[]val={1500, 3000, 2000};
//背包的容量
int m=4;
//物品的个数
int n=w.length;
//创建二维数组,v[i][j] 表示在前i个物品中能够装入容量为j的背包中的最大价值
int[][] v=new int[n+1][m+1];
//为了记录放入商品的情况,我们定一个二维数组
int[][] path=new int[n+1][m+1];
//初始化第一行和第一列
for (int i = 0; i < v.length; i++) {
v[i][0]=0;
}
for (int i = 0; i < v[0].length; i++) {
v[0][i]=0;
}
//根据前面得到公式来动态规划处理
//不处理第一行 i是从1开始的
for (int i = 1; i < v.length; i++) {
//不处理第一列, j是从1开始的
for (int j = 1; j < v[0].length; j++) {
// 因为我们程序i 是从1开始的,因此原来公式中的 w[i] 修改成 w[i-1]
if(w[i-1]> j ){
v[i][j]=v[i-1][j];
}else {
//说明:
//因为我们的i 从1开始的, 因此公式需要调整成:
//v[i][j] = Math.max(v[i - 1][j], val[i - 1] + v[i - 1][j - w[i - 1]]);
//为了记录商品存放到背包的情况,我们不能直接的使用上面的公式,需要使用if-else来体现公式
if(v[i - 1][j]<val[i - 1] + v[i - 1][j - w[i - 1]]){
v[i][j]=val[i - 1] + v[i - 1][j - w[i - 1]];
//把当前的情况记录到path
path[i][j]=1;
}else {
v[i][j]=v[i - 1][j];
}
}
}
}
//输出一下v 看看目前的情况
for(int i =0; i < v.length;i++) {
for(int j = 0; j < v[i].length;j++) {
System.out.print(v[i][j] + " ");
}
System.out.println();
}
System.out.println("============================");
//输出最后我们是放入的哪些商品
//遍历path, 这样输出会把所有的放入情况都得到, 其实我们只需要最后的放入
// for(int i = 0; i < path.length; i++) {
// for(int j=0; j < path[i].length; j++) {
// if(path[i][j] == 1) {
// System.out.printf("第%d个商品放入到背包\n", i);
// }
// }
// }
//行的最大下标
int i = path.length - 1;
//列的最大下标
int j = path[0].length - 1;
//从path的最后开始找
while(i > 0 && j > 0 ) {
if(path[i][j] == 1) {
System.out.printf("第%d个商品放入到背包\n", i);
//计算剩余的空间
j -= w[i-1];
}
i--;
}
}
}
4 KMP算法
4.1 应用场景-字符串匹配问题
字符串匹配问题::
- 有一个字符串 str1= ““硅硅谷 尚硅谷你尚硅 尚硅谷你尚硅谷你尚硅你好””,和一个子串 str2=“尚硅谷你尚硅你”;
- 现在要判断 str1 是否含有 str2, 如果存在,就返回第一次出现的位置, 如果没有,则返回-1。
4.2 暴力匹配算法
如果用暴力匹配的思路,并假设现在str1匹配到 i 位置,子串str2匹配到 j 位置,则有:
- 如果当前字符匹配成功(即str1[i] == str2[j]),则i++,j++,继续匹配下一个字符
- 如果失配(即str1[i]! = str2[j]),令i = i - (j - 1),j = 0。相当于每次匹配失败时,i 回溯,j 被置为0。
- 用暴力方法解决的话就会有大量的回溯,每次只移动一位,若是不匹配,移动到下一位接着判断,浪费了大量的时间。(不可行!)
- 暴力匹配算法实现.
/**
* @author Wnlife
* @create 2020-02-02 21:38
*
* 字符串暴力匹配算法
*/
public class ViolenceMatch {
public static void main(String[] args) {
String str1 = "硅硅谷 尚硅谷你尚硅 尚硅谷你尚硅谷你尚硅你好";
String str2 = "尚硅谷你尚硅你";
int r = volianceMatch(str1, str2);
System.out.println(r);
}
public static int volianceMatch(String str1,String str2){
char[]s1=str1.toCharArray();
char[]s2=str2.toCharArray();
int str1Len=str1.length();
int str2Len=str2.length();
// i索引指向s1
int i=0;
// j索引指向s2
int j=0;
// 保证匹配时,不越界
while (i<str1Len&&j<str2Len){
//匹配成功
if(s1[i]==s2[j]){
i++;
j++;
}else {
//匹配不成功,如果失配(即str1[i]! = str2[j]),令i = i - (j - 1),j = 0。
i=i-(j-1);
j=0;
}
}
//判断是否匹配成功
if(j==str2Len){
return i-j;
}else {
return -1;
}
}
}
4.3 KMP算法介绍
- KMP是一个解决模式串在文本串是否出现过,如果出现过,最早出现的位置的经典算法;
- Knuth-Morris-Pratt 字符串查找算法,简称为 “KMP算法”,常用于在一个文本串S内查找一个模式串P 的出现位置,这个算法由Donald Knuth、Vaughan Pratt、James H. Morris三人于1977年联合发表,故取这3人的姓氏命名此算法;
- KMP方法算法就利用之前判断过信息,通过一个next数组,保存模式串中前后最长公共子序列的长度,每次回溯时,通过next数组找到,前面匹配过的位置,省去了大量的计算时间;
- 参考资料:https://www.cnblogs.com/ZuoAndFutureGirl/p/9028287.html
4.4 KMP算法最佳应用-字符串匹配问题
字符串匹配问题::
1)有一个字符串 str1= “BBC ABCDAB ABCDABCDABDE”,和一个子串 str2=“ABCDABD”
2)现在要判断 str1 是否含有 str2, 如果存在,就返回第一次出现的位置, 如果没有,则返回-1
3)要求:使用KMP算法完成判断,不能使用简单的暴力匹配算法.
思路:
举例来说,有一个字符串 Str1 = “BBC ABCDAB ABCDABCDABDE”,判断,里面是否包含另一个字符串 Str2 = “ABCDABD”?
-
首先,用Str1的第一个字符和Str2的第一个字符去比较,不符合,关键词向后移动一位
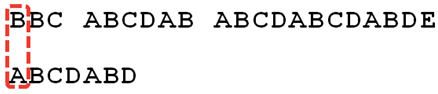
-
重复第一步,还是不符合,再后移 ;

-
一直重复,直到Str1有一个字符与Str2的第一个字符符合为止

-
接着比较字符串和搜索词的下一个字符,还是符合。

-
遇到Str1有一个字符与Str2对应的字符不符合。
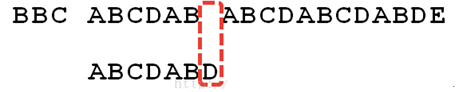
-
这时候,想到的是继续遍历Str1的下一个字符,重复第1步。(其实是很不明智的,因为此时BCD已经比较过了,没有必要再做重复的工作,一个基本事实是,当空格与D不匹配时,你其实知道前面六个字符是”ABCDAB”。KMP 算法的想法是,设法利用这个已知信息,不要把”搜索位置”移回已经比较过的位置,继续把它向后移,这样就提高了效率。)

-
怎么做到把刚刚重复的步骤省略掉?可以对Str2计算出一张《部分匹配表》,这张表的产生在后面介绍

-
已知空格与D不匹配时,前面六个字符”ABCDAB”是匹配的。查表可知,最后一个匹配字符B对应的”部分匹配值”为2,因此按照下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
因为 6 - 2 等于4,所以将搜索词向后移动 4 位。 -
因为空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2(”AB”),对应的”部分匹配值”为0。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移 2 位。

-
因为空格与A不匹配,继续后移一位。

-
逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动 4 位。

-
逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动 7 位,这里就不再重复了。

-
介绍《部分匹配表》怎么产生的
先介绍前缀,后缀是什么
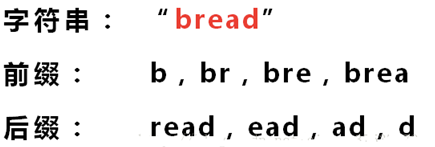
“部分匹配值”就是”前缀”和”后缀”的最长的共有元素的长度。以”ABCDABD”为例,
-”A”的前缀和后缀都为空集,共有元素的长度为0;
-”AB”的前缀为[A],后缀为[B],共有元素的长度为0;
-”ABC”的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
-”ABCD”的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
-”ABCDA”的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为”A”,长度为1;
-”ABCDAB”的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为”AB”,长度为2;
-”ABCDABD”的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。 -
”部分匹配”的实质是,有时候,字符串头部和尾部会有重复。比如,”ABCDAB”之中有两个”AB”,那么它的”部分匹配值”就是2(”AB”的长度)。搜索词移动的时候,第一个”AB”向后移动 4 位(字符串长度-部分匹配值),就可以来到第二个”AB”的位置。

到此KMP算法思想分析完毕!
代码实现:
/**
* @author Wnlife
* @create 2020-02-02 21:52
* <p>
* KMP字符串匹配算法
*/
public class KMPMatch {
public static void main(String[] args) {
// TODO Auto-generated method stub
String str1 = "BBC ABCDAB ABCDABCDABDE";
String str2 = "ABCDABD";
//String str2 = "BBC";
//[0, 1, 2, 0]
int[] next = kmpNext("ABCDABD");
System.out.println("next=" + Arrays.toString(next));
int index = kmpSearch(str1, str2, next);
// 15了
System.out.println("index=" + index);
}
public static int kmpSearch(String str1, String str2, int[] next) {
//遍历
for (int i = 0, j = 0; i < str1.length(); i++) {
//需要处理 str1.charAt(i) != str2.charAt(j), 去调整j的大小
//KMP算法核心点, 可以验证...
while (j > 0 && str1.charAt(i) != str2.charAt(j)) {
j = next[j - 1];
}
if (str1.charAt(i) == str2.charAt(j)) {
j++;
}
if (j == str2.length()) {
return i - j + 1;
}
}
return -1;
}
/**
* 获取到一个字符串(子串) 的部分匹配值表
*
* @param dest 子串
* @return 部分匹配值表
*/
public static int[] kmpNext(String dest) {
//创建一个next 数组保存部分匹配值
int[] next = new int[dest.length()];
//如果字符串是长度为1 部分匹配值就是0
next[0] = 0;
for (int i = 1, j = 0; i < dest.length(); i++) {
//当dest.charAt(i) != dest.charAt(j) ,我们需要从next[j-1]获取新的j
//直到我们发现 有 dest.charAt(i) == dest.charAt(j)成立才退出
//这时kmp算法的核心点
while (j > 0 && dest.charAt(i) != dest.charAt(j)) {
j = next[j - 1];
}
//当dest.charAt(i) == dest.charAt(j) 满足时,部分匹配值就是+1
if (dest.charAt(i) == dest.charAt(j)) {
j++;
}
next[i] = j;
}
return next;
}
}
5 贪心算法
5.1 贪心算法介绍
-
贪婪算法(贪心算法)是指在对问题进行求解时,在每一步选择中都采取最好或者最优(即最有利)的选择,从而希望能够导致结果是最好或者最优的算法;
-
贪婪算法所得到的结果不一定是最优的结果(有时候会是最优解),但是都是相对近似(接近)最优解的结果。
5.2 应用场景-集合覆盖问题
1.假设存在如下表的需要付费的广播台,以及广播台信号可以覆盖的地区。 如何选择最少的广播台,让所有的地区都可以接收到信号;

2. 思路分析:
如何找出覆盖所有地区的广播台的集合呢,使用穷举法实现,列出每个可能的广播台的集合,这被称为幂集。假设总的有n个广播台,则广播台的组合总共有2ⁿ -1 个,假设每秒可以计算10个子集, 如图:

3. 思路分析:
使用贪婪算法,效率高:
目前并没有算法可以快速计算得到准备的值, 使用贪婪算法,则可以得到非常接近的解,并且效率高。选择策略上,因为需要覆盖全部地区的最小集合:
1)遍历所有的广播电台, 找到一个覆盖了最多未覆盖的地区的电台(此电台可能包含一些已覆盖的地区,但没有关系)
2)将这个电台加入到一个集合中(比如ArrayList), 想办法把该电台覆盖的地区在下次比较时去掉。
3)重复第1步直到覆盖了全部的地区
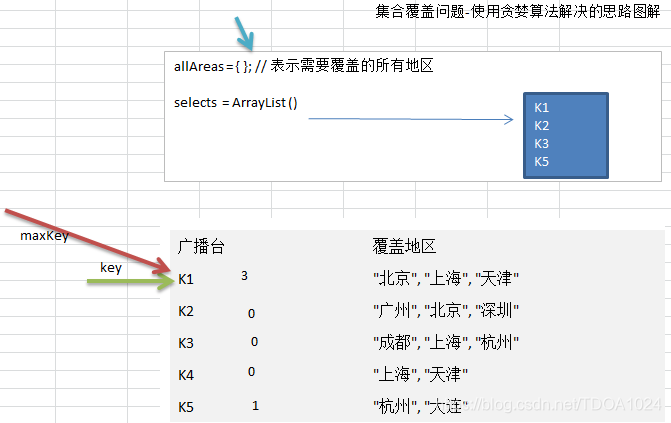
代码演示:
/**
* @author Wnlife
* @create 2020-02-04 16:51
*/
public class GreedyAlgorithm {
public static void main(String[] args) {
//创建一个map,保存每个广播电台和对应的覆盖地区
Map<String, HashSet<String>> broadcast = new HashMap<>(16);
//存储第一个电台对应的覆盖区域
HashSet<String> hashSet1 = new HashSet<>();
hashSet1.add("北京");
hashSet1.add("上海");
hashSet1.add("天津");
//存储第二个电台对应的覆盖区域
HashSet<String> hashSet2 = new HashSet<>();
hashSet2.add("广州");
hashSet2.add("北京");
hashSet2.add("深圳");
//存储第三个电台对应的覆盖区域
HashSet<String> hashSet3 = new HashSet<>();
hashSet3.add("成都");
hashSet3.add("上海");
hashSet3.add("杭州");
//存储第四个电台对应的覆盖区域
HashSet<String> hashSet4 = new HashSet<>();
hashSet4.add("上海");
hashSet4.add("天津");
//存储第五个电台对应的覆盖区域
HashSet<String> hashSet5 = new HashSet<>();
hashSet5.add("杭州");
hashSet5.add("大连");
//加入到map
broadcast.put("k1", hashSet1);
broadcast.put("k2", hashSet2);
broadcast.put("k3", hashSet3);
broadcast.put("k4", hashSet4);
broadcast.put("k5", hashSet5);
//allAreas 存放所有的地区
HashSet<String> allAreas = new HashSet<>();
allAreas.add("北京");
allAreas.add("上海");
allAreas.add("天津");
allAreas.add("广州");
allAreas.add("深圳");
allAreas.add("成都");
allAreas.add("杭州");
allAreas.add("大连");
//存放一个ArrayList存放选择的电台
ArrayList<String> selects = new ArrayList<>();
//定义一个临时的集合,在遍历的过程中,存放遍历过程中的电台覆盖的地区和当前还没有覆盖的地区的交集
HashSet<String> tempSet = new HashSet<>();
//定义给maxKey , 保存在一次遍历过程中,能够覆盖最大未覆盖的地区对应的电台的key
//如果maxKey 不为null , 则会加入到 selects
String maxKey = null;
// 如果allAreas 不为0, 则表示还没有覆盖到所有的地区
while (allAreas.size() != 0) {
//每次循环前,maxKey清空
maxKey = null;
//遍历 broadcasts, 取出对应key
for (String key : broadcast.keySet()) {
//清空tempSet
tempSet.clear();
//取出当前电台对应的覆盖区域
tempSet.addAll(broadcast.get(key));
//当前电台覆盖的区域 和 所有未被覆盖区域的交集
tempSet.retainAll(allAreas);
//如果当前这个集合包含的未覆盖地区的数量,比maxKey指向的集合地区还多,就需要重置maxKey
// tempSet.size() >broadcasts.get(maxKey).size()) 体现出贪心算法的特点,每次都选择最优的
if (tempSet.size() > 0 && (maxKey == null || tempSet.size() > broadcast.get(maxKey).size())) {
maxKey = key;
}
}
//maxKey != null, 就应该将maxKey 加入selects
if(maxKey!=null){
selects.add(maxKey);
//将maxKey指向的广播电台覆盖的地区,从 allAreas 去掉
allAreas.removeAll(broadcast.get(maxKey));
}
}
//[K1,K2,K3,K5]
System.out.println("得到的选择结果是" + selects);
}
}
5.3 贪心算法注意事项和细节
- 贪婪算法所得到的结果不一定是最优的结果(有时候会是最优解),但是都是相对近似(接近)最优解的结果
- 比如上题的算法选出的是K1, K2, K3, K5,符合覆盖了全部的地区
- 但是我们发现 K2, K3,K4,K5 也可以覆盖全部地区,如果K2 的使用成本低于K1,那么我们上题的 K1, K2, K3, K5 虽然是满足条件,但是并不是最优的.
6 普里姆算法
6.1 应用场景-修路问题
看一个应用场景和问题:
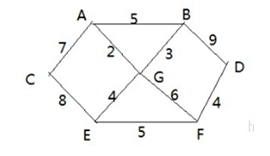
- 有胜利乡有7个村庄(A, B, C, D, E, F, G) ,现在需要修路把7个村庄连通
各个村庄的距离用边线表示(权) ,比如 A – B 距离 5公里 - 问:如何修路保证各个村庄都能连通,并且总的修建公路总里程最短?
- 思路: 将10条边,连接即可,但是总的里程数不是最小.
正确的思路,就是尽可能的选择少的路线,并且每条路线最小,保证总里程数最少.
6.2 最小生成树
修路问题本质就是就是最小生成树问题, 先介绍一下最小生成树(Minimum Cost Spanning Tree),简称MST。
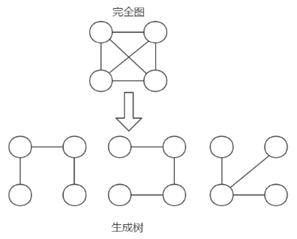
2)给定一个带权的无向连通图,如何选取一棵生成树,使树上所有边上权的总和为最小,这叫最小生成树
2)N个顶点,一定有N-1条边
3)包含全部顶点
4)N-1条边都在图中
5)举例说明(如图:)
6)求最小生成树的算法主要是普里姆算法和克鲁斯卡尔算法
6.3 普里姆算法介绍
- 普利姆(Prim)算法求最小生成树,也就是在包含n个顶点的连通图中,找出只有(n-1)条边包含所有n个顶点的连通子图,也就是所谓的极小连通子图
- 普利姆的算法如下:
1)设G=(V,E)是连通网,T=(U,D)是最小生成树,V,U是顶点集合,E,D是边的集合
2)若从顶点u开始构造最小生成树,则从集合V中取出顶点u放入集合U中,标记顶点v的visited[u]=1
3)若集合U中顶点ui与集合V-U中的顶点vj之间存在边,则寻找这些边中权值最小的边,但不能构成回路,将顶点vj加入集合U中,将边(ui,vj)加入集合D中,标记visited[vj]=1
4)重复步骤②,直到U与V相等,即所有顶点都被标记为访问过,此时D中有n-1条边
5)提示: 单独看步骤很难理解,我们通过代码来讲解,比较好理解.

代码演示:
public class PrimAlgorithm {
public static void main(String[] args) {
//测试看看图是否创建ok
char[] data = new char[]{'A', 'B', 'C', 'D', 'E', 'F', 'G'};
int verxs = data.length;
//邻接矩阵的关系使用二维数组表示,10000这个大数,表示两个点不联通
int[][] weight = new int[][]{
{10000, 5, 7, 10000, 10000, 10000, 2},
{5, 10000, 10000, 9, 10000, 10000, 3},
{7, 10000, 10000, 10000, 8, 10000, 10000},
{10000, 9, 10000, 10000, 10000, 4, 10000},
{10000, 10000, 8, 10000, 10000, 5, 4},
{10000, 10000, 10000, 4, 5, 10000, 6},
{2, 3, 10000, 10000, 4, 6, 10000},};
//创建MGraph对象
MGraph graph = new MGraph(verxs);
//创建一个MinTree对象
MinTree minTree = new MinTree();
minTree.createGraph(graph, verxs, data, weight);
//输出
minTree.showGraph(graph);
//测试普利姆算法
minTree.prim(graph, 0);
}
}
/**
* 创建最小生成树->村庄的图
*/
class MinTree {
//创建图的邻接矩阵
/**
* @param graph 图对象
* @param verxs 图对应的顶点个数
* @param data 图的各个顶点的值
* @param weight 图的邻接矩阵
*/
public void createGraph(MGraph graph, int verxs, char data[], int[][] weight) {
int i, j;
//顶点
for (i = 0; i < verxs; i++) {
graph.data[i] = data[i];
for (j = 0; j < verxs; j++) {
graph.weight[i][j] = weight[i][j];
}
}
}
/**
* 显示图的邻接矩阵
*
* @param graph
*/
public void showGraph(MGraph graph) {
for (int[] link : graph.weight) {
System.out.println(Arrays.toString(link));
}
}
/**
* 编写prim算法,得到最小生成树
*
* @param graph 图
* @param v 表示从图的第几个顶点开始生成'A'->0 'B'->1...
*/
public void prim(MGraph graph, int v) {
//visited[] 标记结点(顶点)是否被访问过
int visited[] = new int[graph.verxs];
//visited[] 默认元素的值都是0, 表示没有访问过
//把当前这个结点标记为已访问
visited[v] = 1;
//h1 和 h2 记录两个顶点的下标
int h1 = -1;
int h2 = -1;
//将 minWeight 初始成一个大数,后面在遍历过程中,会被替换
int minWeight = 10000;
//因为有 graph.verxs顶点,普利姆算法结束后,有 graph.verxs-1边
for (int k = 1; k < graph.verxs; k++) {
//这个是确定每一次生成的子图 ,和哪个结点的距离最近
// i结点表示被访问过的结点
for (int i = 0; i < graph.verxs; i++) {
//j结点表示还没有访问过的结点
for (int j = 0; j < graph.verxs; j++) {
if (visited[i] == 1 && visited[j] == 0 && graph.weight[i][j] < minWeight) {
//替换minWeight(寻找已经访问过的结点和未访问过的结点间的权值最小的边)
minWeight = graph.weight[i][j];
h1 = i;
h2 = j;
}
}
}
//找到一条边是最小
System.out.println("边<" + graph.data[h1] + "," + graph.data[h2] + "> 权值:" + minWeight);
//将当前这个结点标记为已经访问
visited[h2] = 1;
//minWeight 重新设置为最大值 10000
minWeight = 10000;
}
}
}
class MGraph {
//表示图的节点个数
int verxs;
//存放结点数据
char[] data;
//存放边,就是我们的邻接矩阵
int[][] weight;
public MGraph(int verxs) {
this.verxs = verxs;
data = new char[verxs];
weight = new int[verxs][verxs];
}
}





















 9129
9129











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








