LCA最近公共祖先算法

本文来自挑战程序设计竞赛
3种在线算法:
在有根数中，两个节点u和v的公共祖先中距离最近的那个被称为最近公共祖先（LCA，Lowerst Common Ancestor）。用于搞笑计算LCA的算法有许多，在此我们介绍其中的两种。在下文中，我们都假设节点数为n。
1.基于二分搜索的算法
记节点v到根的深度为depth(v)。那么，如果节点w是u和v的公共祖先的话，让u向上走depth(u)-depth(w)步，让v向上走depth(v)-depth(w)步，就都将走到w。因此，首先让u和v中较深的一方向上走|depth(u)-depth(v)|步，再一起一步一步向上走，知道走到同一个节点，就可以在O(depth(u)+depth(v))时间内求出
LCA。

const int MAX_V=100;
vector<int>G[MAX_V];//图的邻接表
int root;//根节点编号

int parent[MAX_V];//父亲节点（根节点的父亲节点记为-1)
int depth[MAX_V];//节点深度

void dfs(int v,int p,int d)//当前节点v，v的父亲节点，v节点所在深度
{
    parent[v]=p;
    depth[v]=d;
    for(int i=0;i<G[v].size();i++)
    {
        if(G[v][i]!=p)
            dfs(G[v][i],v,d+1);
    }
}
void init()
{
    dfs(root,-1,0);//预处理出parent和depth
}
//计算u和v的lca
int lca(int u,int v)
{
    //让u和v向上走到同一深度
    while(depth[u]>depth[v])
        u=parent[u];
    while(depth[v]>depth[u])
        v=parent[v];
    while(u!=v)//找到公共节点
    {
        u=parent[u];
        v=parent[v];
    }
    return u;
}

节点的最大深度是O(n)，所以该算法的时间复杂度也是O(n)。如果只需计算一次LCA的话，这便足够了。但是如果要计算多对节点的LCA的话如何是好呢？刚才的算法，通过不断向上走到同一节点来计算u和v的LCA。这里，到达同一节点后，无论怎么向上走，到达的显然还是同一节点。利用这一点，我们就能够利用二分搜索求出到达公共祖先所需要的最少步数吗？事实上，只要利用如下预处理，就能实现二分搜索。

首先，对于任意顶点v，利用其父亲节点信息，可以用过parent2[v]=parent[parent[v]]得到其向上走两步所到的顶点，在利用这一信息，又可以通过parent4[v]=parent2[parent2[v]]得到向上走4步所到的顶点。以此类推，就能够得到其向上走2^k步索道的顶点parent[k][v]。有了k=floor(log n)以内的所有信息后，就可以二分搜索了，每次的复杂度是O(log n)。另外，预处理parent[k][v]的复杂度是O(nlog n）。
上面的方法也叫调表法。

const int MAX_V=100;
const int MAX_LOG_V=10;
vector<int>G[MAX_V];//图的邻接表
int root;//根节点编号

int parent[MAX_LOG_V][MAX_V];//向上走2^k步所到的节点(超过根时记为-1)
int depth[MAX_V];//节点深度

void dfs(int v,int p,int d)//当前节点v，v的父亲节点，v节点所在深度
{
    parent[0][v]=p;
    depth[v]=d;
    for(int i=0;i<G[v].size();i++)
    {
        if(G[v][i]!=p)
            dfs(G[v][i],v,d+1);
    }
}
void init(int V)
{
    dfs(root,-1,0);//预处理出parent和depth
    for(int k=0;k+1<MAX_LOG_V;k++)
    {
        for(int v=0;v<V;v++)
        {
            if(parent[k][v]<0)//如果父节点是root
                parent[k+1][v]=-1;//那么向上走到2^（k+1）步的父节点也是root
            else
                parent[k+1][v]=parent[k][[parent[k][v]];//否则向上走2^(k+1)步的祖先就是两次向上走2^k的祖先
        }
    }
}
//计算u和v的lca
int lca(int u,int v)
{
    //让u和v向上走到同一深度
    if(depth[u]>depth[v])
        swap(u,v);
    for(int k=0;k<MAX_LOG_V;k++)
    {
        if((depth[v]-depth[u])>>k&1)
            v=parent[k][v];
    }
    if(u==v)
        return u;
    for(int k = MAX_LOG_V-1;k>=0;k--)
    if(parent[k][u]!=parent[k][v])//利用二分搜索计算LCA,其实就是从上往下找根节点
    {
        u=parent[k][u];
        v=parent[v][v];
    }
    return parent[0][u];
}

tarjan离线算法:
具体讲解过程见此文，此文代码并查集用秩优化，已经遍历的根节点用ancestor保存。
http://noalgo.info/476.html
下面是一个朋友写的具体理解，挺不错的。
http://www.cnblogs.com/ixiaoz/p/4728689.html

#include <bits/stdc++.h>
using namespace std;
//fstream input,output;
const int N=40005;
vector<int> v[N];
vector<int> query[N],num[N];
int ans[N],dis[N],father[N];
bool vis[N];
void init(int n)
{
    for(int i=0;i<=n;i++)
    {
        v[i].clear();
        query[i].clear();
        num[i].clear();
        vis[i]=false;
        dis[i]=0;
        father[i]=i;
    }
}
int Find(int x)
{
    if(x==father[x])
        return x;
    return father[x]=Find(father[x]);
}
void Union(int x,int y)
{
    x=Find(x);
    y=Find(y);
    if(x!=y)
        father[y]=x;//不能连反了!
}
void Tarjan(int o)
{
    vis[o]=true;
    for(int i=0;i<v[o].size();i++)
    {
        int tmp=v[o][i];
        if(vis[tmp])
            continue;
        Tarjan(tmp);
        Union(o,tmp);
    }
    for(int i=0;i<query[o].size();i++)
    {
        int tmp = query[o][i];
        if(vis[tmp])
            printf("the root of %d and %d is %d\n",o,tmp,Find(tmp));
    }
}

在线算法：
基于RMQ的算法，将树转为从根DFS标号后得到的序列处理的技巧常常十分有效。对于LCA，利用该技巧也能够高效地计算。首先，按照从根DFS访问的顺序得到顶点序列vs[i]和对应的深度depth[i]。对于每个顶点v，记录其在vs中首次出现的下表为id[v]。

对应的树：

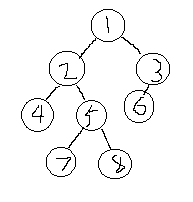
这些都可以在O(n)时间内求得。而LCA(u,v)就是访问u之后到访问v之间所经过顶点中离根最近的那个，假设id[u]<=id[v]，那么有
LCA(u,v)=vs[id[u]<=i<=id[v]中令depth（i)最小的i]
而这可以利用rmq高效的求得。

#include <bits/stdc++.h>
using namespace std;
const int MAX_V=1000;
int root;
int d[10000][20],mark[10000][20];//记录最小值和下标
vector<int> G[MAX_V];
int vs[MAX_V*2-1];//DFS访问顺序
int depth[MAX_V*2-1];//节点的深度
int id[MAX_V];//各个顶点在vs中首次出现的下标
void RMQ_init(const vector<int>& A)//rmq查找区间最小值的代码
{
    int n=A.size();
    for(int i=0;i<n;i++)
    {
        d[i][0]=A[i];
        mark[i][0]=1+i;
    }
    for(int j=1;(1<<j)<=n;j++)
        for(int i=0;i+(1<<j)-1<n;i++)
        {
//          d[i][j]=min(d[i][j-1],d[i+(1<<(j-1))][j-1]);
            if(d[i][j-1]<d[i+(1<<(j-1))][j-1])
            {
                d[i][j]=d[i][j-1];
                mark[i][j]=mark[i][j-1];
            }
            else
            {
                d[i][j]=d[i+(1<<(j-1))][j-1];
                mark[i][j]=mark[i+(1<<(j-1))][j-1];
            }
        }
}
int query(int l,int r)//返回下标
{
    l--,r--;
    int k=0;
    while((1<<(k+1))<=r-l+1)
        k++;
//  return min(d[l][k],d[r-(1<<k)+1][k]);
    if(d[l][k]<d[r-(1<<k)+1][k])
        return mark[l][k];
    else
        return mark[r-(1<<k)+1][k];
}
void dfs(int v,int p,int d,int &k)//节点，父节点，深度，遍历下标
{
    id[v] = k;
    vs[k] = v;
    depth[k++]=d;
    for(int i=0;i<G[v].size();i++)
    {
        if(G[v][i]!=p)
        {
            dfs(G[v][i],v,d+1,k);
            vs[k]=v;
            depth[k++]=d;
        }
    }
}
void init(int v)//初始化，用来记录节点深度和第一次遍历的节点下标等等
{
    int k=0;
    dfs(root,-1,0,k);
    vector<int> de(depth,depth+v*2-1);
    RMQ_init(de);
}
int lca(int u,int v)查询
{
    return vs[query(min(id[u],id[v]),max(id[u],id[v])+1)];
}

其中rmq的查询还可以用线段树来代替。