随机算法 —— 模拟退火

最新推荐文章于 2024-09-09 15:52:08 发布

tham_

最新推荐文章于 2024-09-09 15:52:08 发布

阅读量1.3k

点赞数

分类专栏： Algorithm 文章标签：随机算法模拟退火

Algorithm 专栏收录该内容

29 篇文章 0 订阅

订阅专栏

模拟退火例题：CodeVS: P1344

有 N ( <=20 ) 台 PC 放在机房内，现在要求由你选定一台 PC，用共 N-1 条网线从这台机器开始一台接一台地依次连接他们，最后接到哪个以及连接的顺序也是由你选定的，为了节省材料，网线都拉直。求最少需要一次性购买多长的网线。（说白了，就是找出 N 的一个排列 P1 P2 P3 ..PN 然后 P1 -> P2 -> P3 -> ... -> PN 找出 |P1P2|+|P2P3|+...+|PN-1PN| 长度的最小值)

这种问题被称为最优组合问题。传统的动态规划算法O(n²2ⁿ)在n = 20的情况下空间、时间、精度都不能满足了。这时应该使用比较另类的算法。随机化算法在n比较小的最优化问题表现较好，我们尝试使用随机化算法。

#include<cstdio>
#include<cstdlib>
#include<ctime>
#include<cmath>
#include<algorithm>

const int maxn = 21;
double x[maxn], y[maxn];
double dist[maxn][maxn];
int path[maxn];
int n;
double path_dist(){
    double ans = 0;
    for(int i = 1; i < n; i++) {
        ans += dist[path[i - 1]][path[i]];
    }
    return ans;
}
int main(){
    srand(19260817U);                            // 使用确定的种子初始化随机函数是不错的选择 
    scanf("%d", &n);
    for(int i = 0; i < n; i++) scanf("%lf%lf", x + i, y + i);
    for(int i = 0; i < n; i++) for(int j = i + 1; j < n; j++) dist[i][j] = dist[j][i] = hypot(x[i] - x[j], y[i] - y[j]);
    
    for(int i = 0; i < n; i++) path[i] = i;        // 获取初始排列 
    double ans = path_dist();                    // 初始答案 
    int T = 30000000 / n;                         // 单次计算的复杂度是O(n)，这里的30000000是试出来的 
    while(T--){
        std::random_shuffle(path, path + n);    // 随机打乱排列 
        ans = std::min(ans, path_dist());        // 更新最小值 
    }
    printf("%.2lf", ans);
}

　可惜的是，这个算法只能拿50分。使用O(n!)枚举排列和使用上述算法没有太大的不同。从解的角度分析，假如某一次计算尝试出了一个比较好的路径，那么最优的路径很可能可以在原基础上作一两次改动就可以得到，这时候完全打乱整个序列不是一个很好的选择。

　　另一个方法：根据原序列生成一个新的序列，然后交换新序列的任意两个数。假如说新生成的序列更优，则使用新序列继续计算，否则序列不变。

　　这个算法就是局部搜索法（爬山法）。可惜，这个算法不正确。这个算法只顾眼前，忽略了大局，只要更优便走，这样可能会造成“盯着眼前的小山包，忽略远处的最高峰”，找到的值往往只是“局部最优值”。当然——这个方法也并不是完全不正确。我们可以多次计算使用上述方法计算，取最值。这里不再赘述。

　　下面介绍退火算法（SA,Simulated Annealing）。

　　首先拿爬山做例子：我们要找到山脉的最高峰，但是我（计算机）只能看到我的脚下哪边是上升的，哪边是下降的，看不到远处是否上升。每次移动，我们随机选择一个方向。如果这个方向是上升的的（更优），那么就决定往那个方向走；如果这个方向是下降的（更差），那么“随机地接受”这个方向，接受就走，不接受就再随机一次——这个随机是关键，要考虑很多因素。比如，一个陡的下坡的接受率要比一个缓的下坡要小（因为陡的下坡后是答案的概率小）；同样的下降坡度，接受的概率随时间降低（逐渐降低才能趋向稳定）。

　　为什么要接受一个更差的解呢？如下图所示：

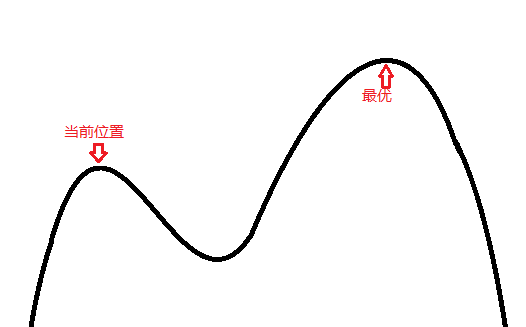
　　如果坚决不接受一个更差的解，那么就会卡在上面的“当前位置”上了。倘若接受多几次更差的解，让他移动到山谷那里，则可以突破局部最优解，得到全局最优解。

既然这个随机这么重要，那么我们就将它写为一个函数：

bool accept(double delta, double temper){
    if(delta <= 0) return true;
    return rand() <= exp((-delta) / temper) * RAND_MAX;
}

　其中delta是新答案的变化量，temper是当前的“温度”。温度是模拟退火算法的一个重要概念，它随时间的推移缓慢减小。我们来分析一下这个代码：

if(delta <= 0) return true;

　　由于答案越小越优，因此当温度的变化量小于零（新答案减小）时，新解比旧解优，因此返回“接受”

return rand() <= exp((-delta) / temper) * RAND_MAX;

　　RAND_MAX是rand()的最大值。为了保证跨平台、跨编译器甚至跨版本时的正常运作，我们不对其作出任何假定。

　　我们把它移项：return (double)rand() / RAND_MAX <= exp((-delta) / temper)。在右边，temper是正数，delta是正数（delta是负数的已经return出去了），因此exp()中间的参数是负数。我们知道，指数函数在参数是负数时返回(0, 1)——这就是接受的概率。我们在左边随机一个实数，如果它比概率小，就接受，否则就不接受。

　　然后将RAND_MAX移到右边，以省下昂贵的除法成本和避免浮点数的各种陷阱。

　　有了接受函数，就可以写计算过程了：

double solve(){
    const double max_temper = 10000;
    double temp = max_temper;
    double dec = 0.999;
    Path p;
    while(temp > 0.1){
        Path p2(p);
        if(accept(p2.dist() - p.dist(), temp)) p = p2;
        temp *= dec;
    }
    return p.dist();
}

　其中Path是路径，它有一个构造函数是接受另一个Path类型的对象，然后交换其中两个点的顺序。

struct Path{
    City path[maxn];
    
    Path(){
        F(i, n) path[i] = citys[i];
    }
    
    Path(const Path& p):path(p.path){
        swap(path[rand() % n], path[rand() % n]);
    }
    
    void shuffle(){
        random_shuffle(path, path + n);
    } 
    
    double dist(){
        double ans = 0;
        for(int i = 1; i < n; i++){
            ans += path[i - 1].distTo(path[i]);
        }
        return ans;
    }
};

其实本代码在很多地方写复杂了，比如累赘的City类。在比赛中，我们不会写得如此复杂。下面对其简化：

#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<cstdio>
using namespace std;

const int maxn = 21;
int n;
double x[maxn], y[maxn];
double dist[maxn][maxn];

struct Path{
    int path[maxn];
    
    Path(){
        for(int i = 0; i < n; i++) path[i] = i;
    }
    
    Path(const Path& p){
        memcpy(path, p.path, sizeof path);
        swap(path[rand() % n], path[rand() % n]);
    }
    
    double dist(){
        double ans = 0;
        for(int i = 1; i < n; i++){
            ans += ::dist[path[i - 1]][path[i]];
        }
        return ans;
    }
};



bool accept(double delta, double temper){
    if(delta <= 0) return true;
    return rand() <= exp((-delta) / temper) * RAND_MAX;
} 

double solve(){
    const double max_temper = 10000;
    const double dec = 0.999;
    double temp = max_temper;
    Path p;
    while(temp > 0.01){
        Path p2(p);
        if(accept(p2.dist() - p.dist(), temp)) p = p2;
        temp *= dec;
    }
    return p.dist();
}

int main(){
    srand(19260817U);
    cin >> n;
    for(int i = 0; i < n; i++) {
        scanf("%lf%lf", x + i, y + i);
    }
    for(int i = 0; i < n; i++){
        dist[i][i] = 0;
        for(int j = i + 1; j < n; j++){
            dist[i][j] = dist[j][i] = hypot(x[i] - x[j], y[i] - y[j]);
        }
    }
    double ans = 1./0;
    int T = 155;
    while(T--){
        ans = min(ans, solve());
    }
    printf("%.2lf", ans);
}

　交上去就可以AC了。

　　由于随机化算法有一定不稳定性，这里要多次调用计算过程取最小值。T=155就是外循环次数。

　　值得注意的是，T=15就可以过80%的数据，T=42可以过完全部数据，此时最大数据运行时间为86ms。这里T取155是保险起见，毕竟时间足够。

　　上面的代码仍有改进的余地。比如，在solve()函数中，应当把最优解记下来，在返回解时返回记下的那个最优解，免得跳到了某些差解后返回差解。

　　下面是一张表供大家估算运行时间，左边是“降温系数”，上方是初温与末温的比值，表格内容是大致的迭代次数。