Pollard Rho 大数分解

最新推荐文章于 2023-06-09 00:03:03 发布
最新推荐文章于 2023-06-09 00:03:03 发布
阅读量1k 收藏 2
点赞数
分类专栏： algorithm_数论 文章标签： Pollard Rho
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/theArcticOcean/article/details/50614033
版权
核心思想：
同时产生多个随机数让差值=goal的概率提高
例子： 在1--1000中随机查找一个数字等于345, p=1/1000
查找两个数字的差是345的概率则是 :

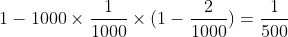
于是通过这种方法也能查找N的因子，通过随机函数和随机数种子来产生一系列的随机数。
随机函数为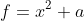 的形式
最开始的随机数通常用2，即 ;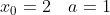
比如查找8051的因子：

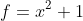
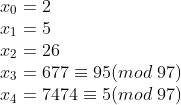（97是8051的因子）

然而出现了f环，这样会无限循环下去。floyd发现了一种方法解决了它。假设两个人A，B沿着同样的路线向前走，后者的速度是前的两倍，当B追上A时，我们知道B已经走了一圈了。
算法实现：
生成两个数字a和b，计算p=(a-b,n)，直到1<p<n, 或者a, b出现循环。如果p=n，那么n是一个质数，否则是n的一个约数，分解递归。
这里的a和b就是用函数f=x^2+1生成的，b=a^2+1.

实现代码： 

#include <iostream>
#include <cstdio>
#include <stdlib.h>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N=6e5;
LL fac[N],num[N];
int cnt;

LL gcd(LL a,LL b){
    return b==0?a:gcd(b,a%b);
}
LL multi(LL a,LL b,LL m){
    LL ans=0;
    while(b){
        if(b&1) ans=(ans+a)%m;
        a=(a+a)%m;
        b>>=1;
    }
    return ans;
}
LL quick_mod(LL a,LL p,LL m){
    LL ans=1;
    while(p){
        if(p&1) ans=multi(ans,a,m);
        a=multi(a,a,m);
        p>>=1;
    }
    return ans;
}
LL Pollard_rho(LL n,LL c){
    LL x,y,k=2,i=1;
    x=rand()%(n-1)+1;
    y=x;
    while(1>0){
        i++;
        x=(multi(x,x,n)+c)%n;
        LL d=gcd((y-x+n)%n,n);
        if(1<d&&d<n) return d;
        if(y==x)  return n;   // 出现循环
        if(i==k) {
            y=x;
            k<<=1;  //x 比y多跑一圈
        }
    }
}
bool Miller_rabin(LL p){
    if(p==2) return 1;
    if(p<2 || (p&1)==0) return 0;
    LL m=p-1;
    int sum=0;
    while((m&1)==0){
        m>>=1;
        sum++;
    }
    for(int i=0;i<10;i++){
        LL a=rand()%(p-1)+1;
        LL x=quick_mod(a,m,p);
        LL g=0;
        for(int j=0;j<sum;j++){
            g=multi(x,x,p);
            if(g==1&&x!=1&&x!=p-1)  return 0;
            x=g;
        }
        if(g!=1) return 0;
    }
    return 1;
}

void find(LL n,LL c){
    if(n==1) return ;
    if(Miller_rabin(n)){
        fac[cnt++]=n;
        return ;
    }
    LL p=n;
    while(p>=n) p=Pollard_rho(p,c--);  //循环避免没找到
    find(p,c);
    find(n/p,c);
}
int main()
{
    //freopen("cin.txt","r",stdin);
    LL x;
    while(cin>>x){
        cnt=0;
        find(x,120);
        sort(fac,fac+cnt);
        memset(num,0,sizeof(num));
        int k=0;
        for(int i=0;i<cnt;i++){
            if(i==0){
                num[k]++;
                continue;
            }

            if(fac[i]==fac[i-1]){
                num[k]++;
            }
            else {
                k++;
                fac[k]=fac[i];
                num[k]++;
            }
        }
        for(int i=0;i<k;i++){
            printf("%lld^%lld*",fac[i],num[i]);
        }
        printf("%lld^%lld\n",fac[k],num[k]);
    }
    return 0;
}
/*
自制数据，经mathematica验证，OK。

In[14]:= FactorInteger[232290989000]

Out[14]= {{2, 3}, {5, 3}, {7, 1}, {61, 1}, {544007, 1}}

In[15]:= FactorInteger[23432590000448]

Out[15]= {{2, 6}, {466201, 1}, {785357, 1}}

In[16]:= FactorInteger[43253245288004]

Out[16]= {{2, 2}, {1493, 1}, {7242673357, 1}}

In[17]:= FactorInteger[200998882133322200]

Out[17]= {{2, 3}, {5, 2}, {29, 1}, {967, 1}, {35837621177, 1}}

In[18]:= FactorInteger[8900446284609340]

Out[18]= {{2, 2}, {5, 1}, {139, 1}, {881, 1}, {3634051513, 1}}

In[19]:= FactorInteger[900046234690488422]

Out[19]= {{2, 1}, {14081, 1}, {31959599271731, 1}}

In[20]:= FactorInteger[4460806408]

Out[20]= {{2, 3}, {3041, 1}, {183361, 1}}

input:
232290989000

23432590000448

43253245288004

200998882133322200

8900446284609340

900046234690488422

4460806408

output:
2^3*5^3*7^1*61^1*544007^1
2^6*466201^1*785357^1
2^2*1493^1*7242673357^1
2^3*5^2*29^1*967^1*35837621177^1
2^2*5^1*139^1*881^1*3634051513^1
2^1*14081^1*31959599271731^1
2^3*3041^1*183361^1

Process returned 0 (0x0)   execution time : 0.305 s
Press any key to continue.
*/

POJ 1811 Prime Test
大意：判断一个数字是否是素数，如果不是输出最小的素因子。 
#include <iostream>
#include <cstdio>
#include <stdlib.h>
using namespace std;
typedef long long LL;
LL min_fac;
LL gcd(LL a,LL b){
    return b==0?a:gcd(b,a%b);
}
LL multi(LL a,LL p,LL m){
    LL ans=0;
    while(p){
        if(p&1) ans=(ans+a)%m;
        a=(a+a)%m;
        p>>=1;
    }
    return ans;
}
LL quick_mod(LL a,LL p,LL m){
    LL ans=1;
    while(p){
        if(p&1) ans=multi(ans,a,m);
        a=multi(a,a,m);
        p>>=1;
    }
    return ans;
}
bool Miller_Rabin(LL p){
     if(p==2) return 1;
     if(p<2 || (p&1)==0) return 0;
     int sum=0;
     LL m=p-1;
     while((m&1)==0){
        m>>=1;
        sum++;
     }
     for(int i=0;i<10;i++){
        LL a=rand()%(p-1)+1;
        LL x=quick_mod(a,m,p);
        LL g=0;
        for(int j=0;j<sum;j++){
            g=multi(x,x,p);
            if(g==1&&x!=1&&x!=p-1) return 0;
            x=g;
        }
        if(g!=1) return 0;
     }
     return 1;
}
LL Pollard_rho(LL n,LL c){
    LL i=1,k=2;
    LL x=rand()%(n-1)+1;
    LL y=x;
    while(1>0){
        i++;
        x=(multi(x,x,n)+c)%n;
        LL d=gcd((y-x+n)%n,n);
        if(d<n&&d>1) return d;
        if(x==y) return n;
        if(i==k){
            y=x;
            k<<=1;
        }
    }
}
void find(LL x,LL c){
    if(x==1) return ;
    if(Miller_Rabin(x)){
        min_fac=min_fac<x?min_fac:x;
        return ;
    }
    LL p=x;
    while(p>=x) p=Pollard_rho(p,c--);
    find(p,c);
    find(x/p,c);
}
int main()
{
    //freopen("cin.txt","r",stdin);
    int t;
    cin>>t;
    while(t--){
        LL x;
        scanf("%lld",&x);
        min_fac=x;
        if(Miller_Rabin(x)) {
            puts("Prime");
            continue;
        }
        find(x,120);
        printf("%lld\n",min_fac);
    }
    return 0;
}

POJ 2429 GCD & LCM Inverse
大意： 给出最大公倍数和最小公约数
求出原来的两个数字，升序输出，有多个的话输出和最小的一个。
分析： gcd(a,b)=G, lcm(a,b)=L 那么L/G=a/G * b/G
如果a+b最小，那么 a/G + b/G也是最小的。a/G * b/G和a/G + b/G有什么联系？在答案一定的情况下，当a/G 和 b/G的差越小，a/G + b/G越大。（周长一定的情况下，圆是面积最大的二维图形）
所以，我们对r=L/G因子分解。找到因子积最大值（<=sqrt(r)） --》 ans
找到这样一个值也需要注意，不是直接排个序，相乘比较就行。比如： 
假设一个值分解成：2 3 4 5  --> 120
LL limit=(LL) sqrt(120)=10
ans=2*3吗？ 显然不是，2*5才是答案 

#include <iostream>
#include <cstdio>
#include <stdlib.h>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long LL;
const int N=5e5+10;
LL fac[N],ff[N],cnt;

LL gcd(LL a,LL b){
    return b==0?a:gcd(b,a%b);
}
LL multi(LL a,LL p,LL m){
    LL ans=0;
    while(p){
        if(p&1) ans=(ans+a)%m;
        a=(a+a)%m;
        p>>=1;
    }
    return ans;
}
LL quick_mod(LL a,LL p,LL m){
    LL ans=1;
    while(p){
        if(p&1) ans=multi(ans,a,m);
        a=multi(a,a,m);
        p>>=1;
    }
    return ans;
}
bool Miller_Rabin(LL p){
     if(p==2) return 1;
     if(p<2 || (p&1)==0) return 0;
     int sum=0;
     LL m=p-1;
     while((m&1)==0){
        m>>=1;
        sum++;
     }
     for(int i=0;i<10;i++){
        LL a=rand()%(p-1)+1;
        LL x=quick_mod(a,m,p);
        LL g=0;
        for(int j=0;j<sum;j++){
            g=multi(x,x,p);
            if(g==1&&x!=1&&x!=p-1) return 0;
            x=g;
        }
        if(g!=1) return 0;
     }
     return 1;
}
LL Pollard_rho(LL n,LL c){
    LL i=1,k=2;
    LL x=rand()%(n-1)+1;
    LL y=x;
    while(1>0){
        i++;
        x=(multi(x,x,n)+c)%n;
        LL d=gcd((y-x+n)%n,n);
        if(d<n&&d>1) return d;
        if(x==y) return n;
        if(i==k){
            y=x;
            k<<=1;
        }
    }
}
void find(LL x,LL c){
    if(x==1) return ;
    if(Miller_Rabin(x)){
        fac[cnt++]=x;
        return ;
    }
    LL p=x;
    while(p>=x) p=Pollard_rho(p,c--);
    find(p,c);
    find(x/p,c);
}
int main()
{
    LL G,L;
    while(cin>>G>>L){
        if(G==L){
            printf("%lld %lld\n",G,L);
            continue;
        }
        LL r=L/G;
        cnt=0;
        find(r,120);
        sort(fac,fac+cnt);
        int top=0;
        for(int i=0;i<cnt;i++){
            if(i==0){
                ff[top]=fac[i];
                continue;
            }
            if(fac[i]==fac[i-1]){
                ff[top]=ff[top]*fac[i];
            }
            else {
                top++;
                ff[top]=fac[i];
            }
        }
        top++;
        LL ans=1,temp=1;
        LL limit=(LL)sqrt(r*1.0);
        for(int i=1;i<(1<<top);i++){
            temp=1;
            for(int j=0;j<top;j++){
                if(i&(1<<j)) temp*=ff[j];
            }
            if(temp<=limit) {
                ans=ans>temp?ans:temp;
            }
        }
        printf("%lld %lld\n",ans*G,r/ans*G);
    }
    return 0;
}




theArcticOcean
关注
  • 0
    点赞
  • 踩
  • 2
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
基于pollard rho方法大数分解算法
01-20
pollard rho方法 floyd循环控制算法 c
Pollard Rho算法浅谈
weixin_30716725的博客
05-26 848
Pollard Rho介绍 Pollard Rho算法是Pollard[1]在1975年[2]发明的一种将大整数因数分解的算法 其中Pollard来源于发明者Pollard的姓，Rho则来自内部伪随机算法固有的循环 Pollard Rho算法在其他因数分解算法[3]中不算太出众，但其空间复杂度Θ(1)的优势和好打的代码使得OIer更倾向于使用Pollard Rho算法 毕竟试除法太慢了，谁...
Pollard Rho算法
思维缜密的博客
01-17 1103
假设一年有n天，房间中有k人，每个人的生日在这n天中，服从均匀分布，两个人的生日相互独立问至少要有多少人，才能使其中两个人生日相同的概率达到p解：考虑k≤n设k个人生日互不相同为事件A，则PAnn​nn−1​⋯nn−k1​由题意PA≤1−p,由1x≤exPA≤e−n1​e−n2​⋯enk−1​e−2nkk−1​≤1−p解得k≥211−2nln。
Pollard rho算法总结
Harris-H的博客
07-06 653
Pollard rho算法总结 前置知识 快速幂 快速乘 Miller Rrabin判断素数O(klog3n)O(klog^3n)O(klog3n) 快速幂 太简单了，不讲 ll ksm(ll a,ll n,ll p){ ll s=1; while(n){ if(n&1) s=qmul(s,a,p); a=qmul(a,a,p); n>>=1; } return s; } 快速乘 比较简单，就转化为long double 在转换为longlong 自然溢出 差
Pollard Rho因子分解算法
weixin_30335353的博客
02-09 301
　　有一类问题，要求我们将一个正整数x，分解为两个非平凡因子（平凡因子为1与x）的乘积x=ab。 　　显然我们需要先检测x是否为素数（如果是素数将无解），可以使用Miller-Rabin算法来进行测试。 　　Pollard Rho是一个非常玄学的方式，用于在O(n^1/4)的期望时间复杂度内计算合数n的某个非平凡因子。事实上算法导论给出的是O(√p)，p是n的某个最小因子，满足p与n/p互质。...
Pollard-Rho算法详解
09-12
Pollard-Rho算法详解
Pollard Rho算法思想
07-28
Pollard Rho算法思想
RhoPollard_Factorize:Java 多线程 Rho Pollard 分解算法
06-25
RhoPollard_Factorize Java RhoPollard 分解算法，在单线程和多线程中实现。
pollard-rho-factoriser:使用 Miller-Rabin 检验的 Pollard-Rho 数因子分解器
06-11
波拉德-rho-分解器使用 Pollard-Rho 算法将数字分解为质因数，并使用 Miller-Rabin 检验验证质数。 当前编程为在作为参数给出的范围内SSN * (10 ^ 6 + j) + i 。 二次筛未实施。
RSA算法的纯Python实现
05-28
RSA算法的纯Python实现，压缩包内共4个文件，分别是 1、大整数的运算库（当然不是算加减乘除的，这个python本身就有）。这个库是计算乘模运算，幂模运算（蒙哥马利算法），最大公约数算法及扩展最大公约数算法（扩展欧几里得算法）等。 2、质数库。Miller_Rabin素数判断法，大整数快速因式分解算法（pollard_rho算法），生成指定位数的大质数或大整数算法等。 3、RSA算法库。使用上面两个库，实现RSA算法。实现了生成指定数位的密钥对，加密，解密，签名和验证，这5个核心功能。 4、RSAtest.py一个使用RSA算法库的例子。例子从生成密钥对开始，对数据进行加解密，签名和验证签名，最后用修改后的消息再次验证签名。 这个RSA算法最低支持32位密钥长度，最长没限制。但是事实上，在我的电脑上测试，1024位大概1.3秒左右，1536大约5~6秒，2048位密钥生成就需要约27秒。
大数分解（基于非常大的整数的分解）
11-28
对大整数进行分解！
64位以内Rabin-Miller 强伪素数测试和Pollard rho 因数分解算法的实现
10-22
64位以内Rabin-Miller 强伪素数测试和Pollard rho 因数分解算法的实现的C代码
分解因子算法——Pollard rho算法
国科大网安二班的博客
03-22 2816
分解因子算法——Pollard ρ\rhoρ 算法 攻击RSA密码体制最明显的方法就是分解大整数。关于大整数分解的算法有许多，常见的有试除法、p±1p\pm1p±1算法、Pollard ρ\rhoρ算法、数域筛法、二次筛法等等。这篇分享的就是其中之一的Pollard ρ\rhoρ算法。 我们说因子分解，很多时候并不一定要把大整数nnn彻底分解成素数乘积，而是求出nnn的某个非平凡因子即可。求大整数的一个因子固然困难，但是Euclidean算法告诉我们求两个数的最大公因子是可以在O(log⁡n)O(\log
唯一分解之Pollard-Rho算法
这里RevolIA，_(:з」∠)_
02-02 1428
一般分解是的复杂度，那么Pollard-Rho复杂度大概是，嗯就是x的四分之一次方，也就是说即使是longlong 的极限1e18，也能1s内跑的出来（18/4 = 4.5） 原理： 对于一个大整数n，我们取任意一个数x是n的质因数的几率很小， 如果取两个数x1以及x2使得它们的差是n的因数，那么几率就提高了， 如果取x1以及x2使得gcd((x1−x2),n)>1的概率就更高了。（...
pollard_rho学习笔记 数论
forever_shi的博客
06-02 1503
pollard_rho算法是用来解决质因数分解问题的。 我们知道，朴素的质因数分解是O(n−−√)O(n)O(\sqrt{n})的，但是如果nnn很大的话应该怎么办呢？这时候就要用到pollard_rho了。 pollard_rho也是一种基于随机的算法，它的思路是先用miller_rabin来判断当前数是否已经是素数了，如果是的话记录并返回。如果不是，我们设要分解的数为nnn,那么我们考虑去...
$PollardRho$ 算法及其优化详解
weixin_30415801的博客
03-16 601
\(PollardRho\) 算法总结： Pollard Rho是一个非常玄学的算法，用于在\(O(n^{1/4})\)的期望时间复杂度内计算合数n的某个非平凡因子（除了1和它本身以外能整除它的数）。事实上算法导论给出的是\(O(\sqrt p)\)，\(p\)是\(n\)的某个最小因子，满足\(p\)与\(n/p\)互质。但是这些都是期望，未必符合实际。但事实上Pollard Rho算法在实际环...
Pollard’s rho算法
最新发布
永远相信美好的事情即将发生
06-09 484
给定一正整数N∈N∗，试快速找到它的一个因数。很久很久以前，我们曾学过试除法来解决这个问题。很容易想到因数是成对称分布的：即N1N​和N​N。这个很容易想清楚，我们只需要把区间1N​扫一遍就可以了，此时试除法的时间复杂度为ON​。对于N≥1018的数据，这个算法运行起来无疑是非常糟糕的。我们希望有更快的算法。对于这样的算法，一个比较好的想法是去设计一个随机程序，随便猜一个因数。如果你运气好，这个程序的时间复杂度下限为O1。但对于一个N≥10。
Pollard rho 算法求解离散对数问题
国科大网安二班的博客
02-28 3688
Pollard ρ\rhoρ 算法求解离散对数问题 离散对数(DLP)问题：设有群(G,⋅)(G,\cdot)(G,⋅)，α∈G\alpha \in Gα∈G是一个nnn阶元素。给定β∈<α>\beta \in \left< \alpha \right>β∈⟨α⟩，找到指数c，0≤c≤n−1c，0\le c\le n-1c，0≤c≤n−1，满足 αc=β \alpha ^{c} =\beta αc=β 前面分享过因子分解的Pollard ρ\rhoρ 算法（为了更好地理解Pollar
【模板】Pollard-Rho算法
C202044zxy的博客
09-18 644
一、题目 电磁看题 二、解法 作者讲的解法只是一个缩略版，要想获得更好的理解请参照大佬的博客。 0x01 生日悖论 如果你不是很了解，点此观看 生日悖论告诉了我们一个道理，也就是我们用组合计算的方式会比单个确切值更有概率得到答案。什么意思呢？举个例子，我们要找到xxx，用r−lr-lr−l的方式比直接randrandrand概率有更大概率得到xxx，这里作者就不给详细证明了，感性理解。 所以与其直...
大数分解的时间复杂度为多少
06-07
对于一般的大数分解问题，它的时间...因此，对于大数分解问题，我们通常采用一些特殊的技巧来加速计算，例如分解质因数、Pollard-rho算法等。这些算法的时间复杂度虽然也很高，但通常比一般的大数分解算法要快得多。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值