欧拉方法python代码实现

如有不对，请批评指正！

1. 显式Euler和隐式Euler

2. 改进的Euler

3. 龙格-库塔（Runge-Kutta）

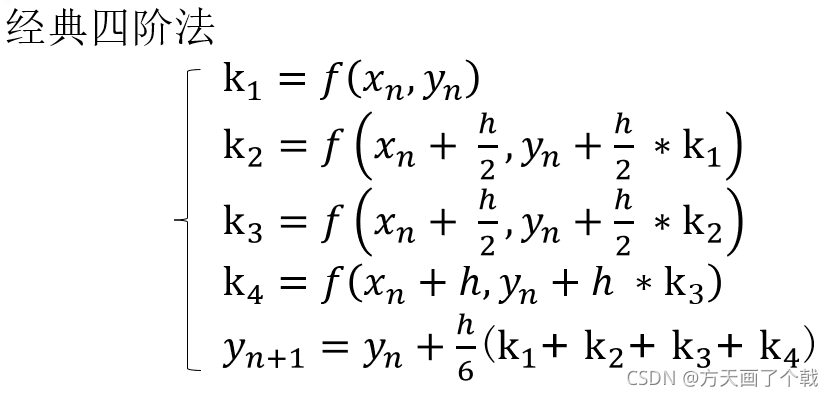
4. 举个栗子

代码仅为了说明计算过程，并未进行优化！

import math
import matplotlib.pyplot as plt

y_e = []  # 显式
y_i = []  # 隐式
y_pro = []  # 改进
y_p = []  # 改进
y_rk = []  # 龙格-库塔
y_c = []  # 解析解
x = []
h = 0.1  # 步长
num = 20


def fun(x0, y0):
    return -2 * x0 / y0 + y0


def Euler():
    print('{:>3s}{:>8s}{:>9s}{:>12s}{:>9s}{:>9s}'.format('x', 'y_e', 'y_i', 'y_pro', 'y_rk', 'y_c'))
    for i in range(num):
        # 显示Euler
        y_e.append(round(y_e[i] + h * fun(x[i], y_e[i]), 5))

        # 隐式Euler
        y_i1 = y_i[i] + h * fun(x[i], y_i[i])
        y_i2 = y_i[i] + h * fun(x[i + 1], y_i1)
        while abs(y_i2 - y_i1) > 1e-6:
            y_i1 = y_i2
            y_i2 = y_i[i] + h * fun(x[i + 1], y_i1)
        y_i.append(y_i2)

        # 改进Euler
        y_p.append(y_pro[i] + h * fun(x[i], y_pro[i]))
        y_pro.append(round(y_pro[i] + h / 2 * (fun(x[i], y_pro[i]) + fun(x[i + 1], y_p[i])), 5))

        # 龙格-库塔
        k1 = fun(x[i], y_rk[i])
        k2 = fun(x[i] + h / 2, y_rk[i] + h / 2 * k1)
        k3 = fun(x[i] + h / 2, y_rk[i] + h / 2 * k2)
        k4 = fun(x[i] + h, y_rk[i] + h * k3)
        y_rk.append(round(y_rk[i] + h / 6 * (k1 + 2 * k2 + 2 * k3 + k4), 5))

        # 解析解
        y_c.append(round(math.sqrt(1 + 2 * x[i + 1]), 5))

        print('{}{:>10f}{:>10f}{:>10f}{:>10f}{:>10f}\n'.format(
            round(x[i + 1], 1),
            y_e[i + 1],
            y_i[i + 1],
            y_pro[i + 1],
            y_rk[i + 1],
            y_c[i + 1]))

    plt.plot(x, y_e, label='Euler_Explicit', color='r', marker='+')
    plt.plot(x, y_i, label='Euler_Implicit', color='c', marker='>')
    plt.plot(x, y_pro, label='Euler_Improvement', color='b', marker='3')
    plt.plot(x, y_rk, label='Euler_RungeKutta', color='m', marker='d')
    plt.plot(x, y_c, label='Analytical solution', color='g', marker='o')
    plt.legend()
    plt.show()


if __name__ == '__main__':
    # 初始值
    x.append(0.0)
    y_e.append(1)  # 显式
    y_i.append(1)  # 隐式
    y_pro.append(1)  # 改进
    y_rk.append(1)  # 龙格-库塔
    y_c.append(1)  # 解析解
    for i in range(num):
        x.append(round(x[0] + (i + 1) * h, 1))
    Euler()

5. 运行结果

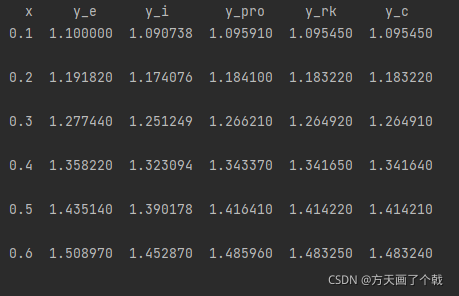
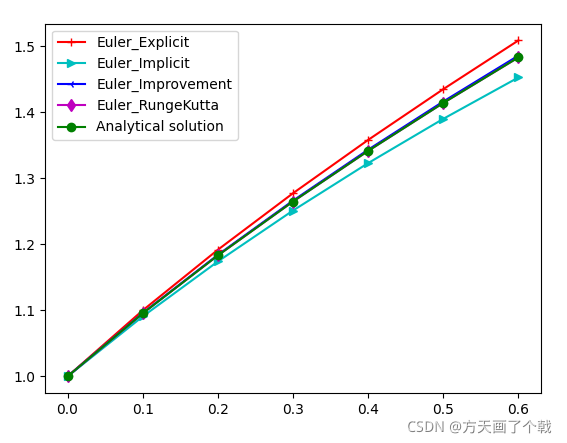
num = 6时

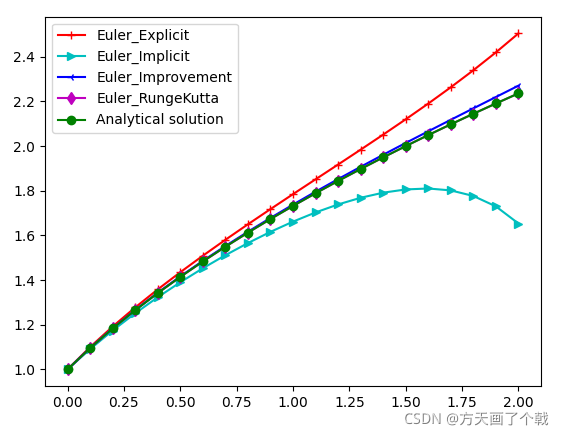
num = 20

参考：代码实现：显示欧拉、隐式欧拉、改进欧拉、龙格库塔法

如有不对，敬请批评指正！
（转载文章请注明作者和出处）