从网上搜了半天也没几篇关于MIS多重重要性采样有关的文章,着实有些不解。这么重要的技术,为什么仅仅存在于论文的世界里呢?
作为上个世纪末一篇流芳几十年的博士论文,发表在SIGGRAPH上,即《Robust Monte Carlo Methods for Light Transport Simulation》这部承前启后的开山之作,里面提出的最重要的方法之一就是MIS算法,既然没有多少人写,那我就自己来写一下吧,打算好好整理整理这种方法的思想和算法公式。
本文需要提前了解什么是蒙特卡洛算法,以及什么是重要性采样,以及什么是蒙特卡洛光线追踪技术。
本文会写个小例子对比多重重要性采样技术的优点
目录
一、采样光源和采样BRDF
学过光线追踪的人都知道,MCRT一共有两种方法进行采样:
一种是采样BRDF:即根据表面散射分布概率,来发射相应概率的采样光纤。例如对于严格的镜面,根据其BRDF就往它的镜面反射方向发射采样ray就好了:

对于极其粗糙的面,我们设置BRDF在各个方向的概率都一样,也就是随机向四周任意方向发射采样ray即可。注意BRDF和BSDF简单区分的话其实都一样,散射和反射本身也是指代的同一种效应。
另一种是采样光:即在某个散射点上,我们直接从光上进行采样,然后计算采样到光采样点的概率,用来作为MCRT的计算输入。
这两种方法的比较:

从上到下,平板的粗糙度一直在增加。
出现上面的现象的原因是,当采样BSDF时,比较粗糙的面就不容易采样到光源,尤其是光源比较小的时候。
而采样光源时,对于比较大的光源,采样的方向和镜面光方向一旦差别比较大就不算采样到,所以光滑的平板不容易采样到光源:比如RT追踪到一个散射点,然后朝着光源散射,然后从光源采样,但是从光源采样到的点不一定能根据BSDF(因为比较光滑,类似镜面反射)反射到人眼。
二、两种策略的对比分析
首先这两种策略都是重要性采样技术:都是作用在某个散射点上的采样技术,只是对应不同的情况,它们的采样方差不一样。对于粗糙面来说,BSDF采样的方差会大很多,这是因为BSDF采样的Ray比较发散,很难对准比较小的光源位置。
所以我们需要认识到,这两种采样技术,其实都是运用在某个散射点上的不同的概率分布罢了。
其实我们完全可以针对某物体的粗糙度来选择使用哪种策略——这肯定是可以的,比较粗糙的,同时光源比较小的时候,就用采样光的技术;比较光滑的,同时光源比较大,就用采样BSDF的技术。但是,对于多光源场景,以及光源大小如何判断等问题,以及如何确定光滑与不光滑的阈值等,这种方法是没有解决的办法的。
对于渲染方程,我们惟一的目标就是要计算其积分值,而采样的意义也是为了尽可能快地收敛到我们想要的结果,哪怕这个结果只是在不断逼近而可能永远也到达不了真实值(对光线追踪来说,尤其是基于场景的渲染(IBL)技术,即使忽略场景本应该是连续的,除非把所有的光源代表的离散点都采样一遍,否则根本无法得到精准的渲染结果)。
采样BRDF:这个概率密度就是由BRDF决定的。

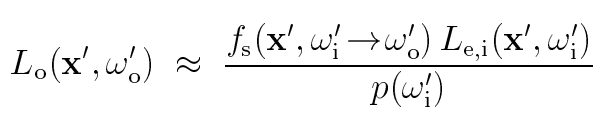
采样光源:这个概率密度是由光到散射点的距离以及夹角决定的。

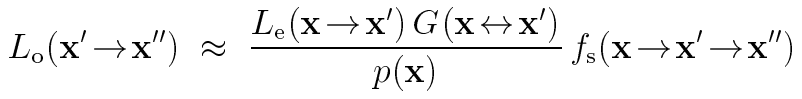
例如,BSDF采样策略可以表示为光源表面上的分布,使用关系式:

该公式使方向密度转化为区域密度成为可能,其实这个关系式表示的就是:
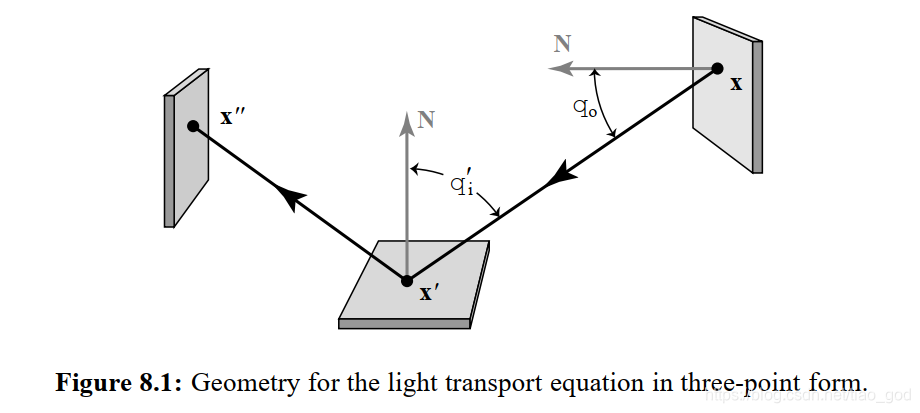
其中注意![]() 代表这个方向的垂直立体角:
代表这个方向的垂直立体角:

从而将两种采样策略表示为同一域上不同的概率分布。
上面的式子因为不太好表述,所以就这样简单地写一下,如果以后有时间,我会重新构思一下怎么介绍这些公式的由来。
三、问题的提出
我们一般要求积分的方程比较复杂,例如前面的光亮度积分,不同场景需要考虑不同的材质和光的位置,所以很难设计比较好的采样策略。
主要的问题是,我们希望在整个参数值范围内得到低方差的结果,也就是说,当这些参数变化时,得到的所有可能的被积函数:
 例如某个函数是红色函数和绿色函数的组合函数。
例如某个函数是红色函数和绿色函数的组合函数。
不幸的是,要做到这一点往往很困难。问题是被积函数通常是许多不同因子的和或积,并且过于复杂,无法直接从中采样。
相反,样本是从密度函数中选择的,该密度函数与因子的某个子集成比例(如上文所述的BSDF采样策略)。当一个未考虑的因素对被积函数有很大影响时,这可能导致高方差。(比如前面我们在积分光源的时候有时候只考虑了对光源重要性采样,有时候只考虑了对BRDF重要性采样)。
针对这类集成问题,提出了一种新的策略,称为多重重要性抽样。它基于使用几种不同的技术进行采样的思想,旨在对被积函数的不同特征进行采样。例如,假设被积函数的形式
![]()
而且其中的每个![]() 都是已知形式的,我们就可以找到对应于每个
都是已知形式的,我们就可以找到对应于每个![]() 的合适的采样概率点
的合适的采样概率点![]() ,
,
我们主要关注的不是如何构造一套合适的抽样技术,甚至不是如何确定从每一种技术中应抽取的样本数量。相反,我们考虑的问题是,一旦采集了这些属于不同概率密度的样本,它们应该如何组合。将展示如何以一种无偏的方式来做到这一点,并且方差可以证明是接近最优的。例如,在光泽高光问题中,我们建议同时使用BSDF和光源采样策略进行采样。然后,我们展示如何自动组合这些样本,以获得整个表面粗糙度和光源参数范围内的低方差结果。
四、多重重要性采样
使用超过一种采样技术,可以让MC的鲁棒性更好,但是重点在于怎么把采样的样本进行组合。
- multi-sample model:组合样本的任意无偏方法可以被表示为权重函数,这给了我们一个很大的空间去探索可能的组合策略,以及一个统一的表示方法。我们提出了一个可证明的好的组合样本的策略,我们称之为balance heuristic。我们证明了这种方法在一个小的加法项内给出了一个比任何其他无偏组合策略都小的方差。该方法简单实用,可使蒙特卡罗计算更具鲁棒性。我们还提出了其他几种组合策略,这些策略基本上是balance heuristic算法的改进:它们在一般情况下保留了其可证明的良好行为,但在普通的特殊情况下被设计为具有较低的方差。因此,在实践中,它们通常比balance heuristic法更可取。
- 最后,我们考虑了一种不同的模型,即one-sample model模型。在该模型下,通过随机选择一种非采样技术,然后从中提取单个样本来估计积分。再次,我们考虑如何通过加权样本来最小化方差,并且我们证明对于这个模型,balance heuristic是最优的。
- 注意,这里所说的单采样和多采样模型,不是说单采样只采样一次,而是说一次采样以后通过多个PDF进行加权。
多采样模型
需要一个精确的模型来表示我们的采样点是如何获得和被组合了。我们将使用下面描述的多样本模型。该模型允许将任何无偏组合策略编码为一组加权函数。
假如我们要对f(x)进行积分:
 ,
,
其中,对于![]() , 采样概率密度
, 采样概率密度![]() 是知道的,而且可以通过
是知道的,而且可以通过![]() 产生任意的样本分布。
产生任意的样本分布。
假设ni是从概率密度pi中产生的样本的数量,设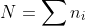 代表样本的总元素数。我们假设每种技术的样本数是预先确定的,然后再抽取任何样本。(我们不考虑如何在各种技术之间分配样本的问题,这本身是一个有趣的问题,将在后面进一步讨论)来自采样技术 i 的样本表示为
代表样本的总元素数。我们假设每种技术的样本数是预先确定的,然后再抽取任何样本。(我们不考虑如何在各种技术之间分配样本的问题,这本身是一个有趣的问题,将在后面进一步讨论)来自采样技术 i 的样本表示为 ,j 表示 1 到 ni。假设所有样本都是独立的,即生成新的随机数来控制去选择哪个样本。
,j 表示 1 到 ni。假设所有样本都是独立的,即生成新的随机数来控制去选择哪个样本。
如何用 来得到积分值呢,我们需要一种无偏的策略来组合这些样本。我们假设这些样本的权重是不同的,取决于 pi ,故我们用 wi 来表示采用 pi 概率密度进行采样得到的样本,在组合策略中的权重:
来得到积分值呢,我们需要一种无偏的策略来组合这些样本。我们假设这些样本的权重是不同的,取决于 pi ,故我们用 wi 来表示采用 pi 概率密度进行采样得到的样本,在组合策略中的权重:
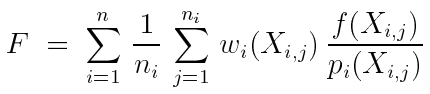
这个公式可以理解为使用一定的权重项来组合 ![]() ,进行估计。因为是无偏的,所以说有两点必须要满足:
,进行估计。因为是无偏的,所以说有两点必须要满足:
这说明,在![]() 的采样点处一定有至少一个样本的 pi 不为0,即一定能在那个不为0的 x 点产生样本。因此对任意的 pi ,能够采样整个邻域都是不必须的(因为会有别的pi概率能够采样到)。pi 作为集中在被积函数特定区域的特殊采样技术。
的采样点处一定有至少一个样本的 pi 不为0,即一定能在那个不为0的 x 点产生样本。因此对任意的 pi ,能够采样整个邻域都是不必须的(因为会有别的pi概率能够采样到)。pi 作为集中在被积函数特定区域的特殊采样技术。
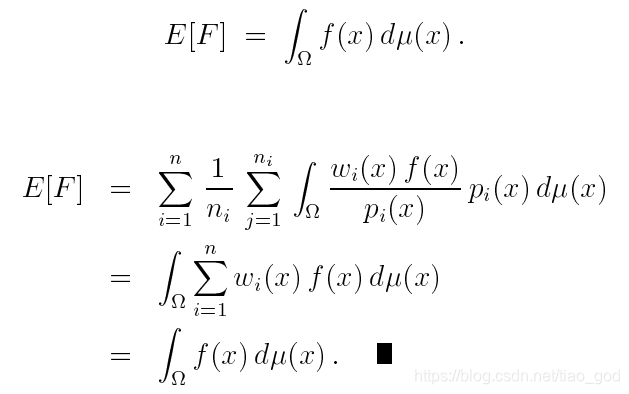
通过合理的采选择权重函数,很容易去表示任何无偏的策略。首先是一些可能的例子,以及如何用权重函数来表示它们。以及通过一种新的组合策略,证明该策略提供了比其他任何表示都要好的性能。
可以采用的权重函数举例
假如我们有三个采样技术 p1,p2,p3,以及每个技术只采样一个样本,最终的估计值为:
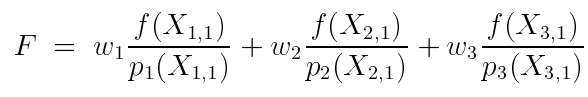
它相当于是![]() 估计器的加权组合。(注意这个时候的权重值是我们随便选取的,只要它们加起来等于1就行了)
估计器的加权组合。(注意这个时候的权重值是我们随便选取的,只要它们加起来等于1就行了)
但是这种估计器可能因为某个采样技术的方差过大导致结果很不好:
![]()
另一种可能的组合策略是在采样技术中划分域,注意这些域之间是不重叠的。

对于权重函数来说:

例如,通常通过将场景划分为光源区域和非光源区域来评估散射方程,这两个区域使用不同的技术进行采样。。根据场景的几何体和材质,这种固定的划分可能会导致比所需的大得多的方差(如我们在高光示例中看到的采样效果很差的例子)。
图形中经常使用的另一种组合技术是将被积函数写为一个和的形式:
![]()
并使用不同的采样技术来估计每个gi的贡献。例如,当BSDF被拆分为漫反射、光泽度和镜面反射组件时,会发生这种情况,它们的贡献将分别估计(通过从密度函数pi/gi采样)。与前面一样,将此策略表示为一组加权函数是很简单的。
多样本模型的产生
多样本估计器可以写为:

其中![]() 表示的是样本贡献。
表示的是样本贡献。![]() 是任意的,但是为了满足无偏估计,
是任意的,但是为了满足无偏估计,

多样本模型可以表示任何无偏组合策略,要保证每个基于某种概率密度样本的采样都是独立的。由上面的公式可以知道:

只要这里的 wi 满足前面所述的对权重的两个要求,结果就一定是无偏的。
balance heuristic
前面写的多采样方法给出了无偏估计器的表示形式,这里我们需要找到其中方差最小的无偏估计器。
我们最终会得到这种权重函数 : 
由balance可以知道,
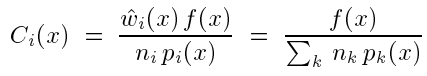 这里的关于样本的贡献项Ci并不取决于产生它的技术(参考上面的式子,其与pi无关)。
这里的关于样本的贡献项Ci并不取决于产生它的技术(参考上面的式子,其与pi无关)。
这个估计器的特点是,没有比它更好的组合方案了。
该定理的理解
令 为上面所述的权重函数
为上面所述的权重函数 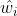 的采样器,令
的采样器,令 为任意的无偏估计器,
为任意的无偏估计器,
 其中
其中 ![]() 表示期望估计值(论文有该定理的证明,这里就不再赘述了)
表示期望估计值(论文有该定理的证明,这里就不再赘述了)
虽然该函数表示的是小于等于,我们可以了解到,就算再好的采样组合技术,也不会比现在的技术有多大的提升了。当然我们知道假如某种产生的概率密度函数和被积函数是成比例的,则最好的方法就是直接使用当前的pi技术来估计,忽略其他的估计器,但是这种情况一般是不可知的,就算相比于最好的估计器,该估计器的方差比它再差也差不过右边的项。
请注意,随着每种技术的样本数增加,方差差距变为零。另一方面,如果使用一个糟糕的组合策略,那么方差可以比最优值大任意数量。
这基本上就是我们在高光图像中观察到的:如果使用错误的样本来估计积分,方差可能会比  大几十倍或几百倍。
大几十倍或几百倍。
但是在计算中,我们不光要计算当前pi产生Xi,j的概率,我们还得把其他n-1种技术产生Xi,j的概率计算出来。这样做通常很简单;这只是重新组织计算概率的例程,并将所有密度表示为同一度量。
为了计算每个采样点x的加权函数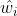 ,我们计算了两种抽样技术产生x的概率密度。因此,如果x是通过对光源进行采样而生成的,那么我们也可以通过对BSDF进行采样来计算产生相同点x的概率密度。请注意,与其他计算(如光线投射到物体上的计算)相比,计算这些额外概率的成本微不足道。
,我们计算了两种抽样技术产生x的概率密度。因此,如果x是通过对光源进行采样而生成的,那么我们也可以通过对BSDF进行采样来计算产生相同点x的概率密度。请注意,与其他计算(如光线投射到物体上的计算)相比,计算这些额外概率的成本微不足道。


其中,![]() 表示总的采样样本数,
表示总的采样样本数,![]() 表示用每种采样技术分别占总采样样本数的比例。
表示用每种采样技术分别占总采样样本数的比例。
这种组合技术也可以理解为一个标准的MC采样估计器:
 表示给定点x取样的概率密度,取整个n样本序列的平均值。
表示给定点x取样的概率密度,取整个n样本序列的平均值。
因此,balance heuristic是组合样本的自然方法。它具有标准蒙特卡罗估计量的形式,其中分母p^表示应用它的整个样本组的平均分布。下图给出了该估计器的伪代码:

然而,重要的是要认识到这种估计器的主要优点不是它简单或标准,而是它与其他组合策略相比具有可证明的良好性能。这就是我们在加权函数方面引入更复杂的公式的原因,以便我们可以将其与其他组合策略进行比较。
提升的组合策略
尽管balance heuristic 是一个很好的组合策略,但是仍有提高的空间。这里我们讨论两种有更低方差的估计器。
我们表明,在原始采样技术非常好的情况下,例如光源采样产生低方差结果的情况下,balance heuristic会导致比必要的更多的方差(因为平衡,会把其他估计器的方差引进来)。问题是,由于平衡启发式的附加方差是加性的:当最优估计量已经有很大的方差时,这并不显著,但是与方差很低的最优估计量相比,这是明显的。因此我们讨论一下在低方差情况下(一种估计器很适合被积函数,而且比其他的都好太多的时候)应该如何改变权重函数。(实际上,表现出来的就是我们会让权重函数区别更大,有的权重非常小,趋近于0,有的权重非常大,趋近于1)。这两种方法,叫cutoff 和 power heuristics,balance heuristic 可以作为这两类估计量族的一个极限情况得到。最后我们证明这两类估计器在理论上应该是最优的,而且从来不会比balance heuristic差,而且对于低方差问题,可以表现得更好。
我们还做了很多实验来验证理论,基于这些实验,我们发现有一种策略在实践中是一个很好的选择:即指数为2的power heuristic 。

此图像是使用BSDF采样策略和光源采样策略渲染的。这些样本与前面的图的完全相同,只是这里使用balance heuristic将两种样本组合起来。这就产生了一种对整个光泽表面和光源几何形状都有效的策略。
低方差问题的例子和分析
虽然使用平衡启发(balance heuristic)对上面的效果很好,但是对比特定情况的最优采样器而言,并不是特别好:(这里每个像素只用每种技术采样一个值)

这种情况,在采用的所有采样技术中,某一种技术明显特别好的时候会出现。即使平衡启发的方差已经很低了,但是在采样次数比较少的时候,它和最优采样器之间的差距还是非常地大。不幸的是,在多样本模型的点抽样假设下,没有办法可靠地检测到这种情况。相反,我们的策略是使用所有给定的技术获取样本,并计算权重函数,自动将低权重分配给任何不相关的样本。毕竟我们不知道哪种采样技术最好,所以说我们也很难去从中找到最适合的技术。
下图表示分别用两种密度函数来采样求f的积分值。

在这种情况下,很明显我们如果让采样p1的权重为1,采样p2的权重为0的话,可以得到最好的估计结果。而平衡启发要考虑两种采样技术,所以会引入额外的方差。

如上图我们把采样区域分成A和B两部分,其中属于B的部分p2>p1,属于A的部分p1>p2。然后我们分别用两种采样技术采样一个数据:
- 首先考虑p1,采样p1数据的可能性出现在A中的概率更大,权重
 接近于1,接近于最优采样。
接近于1,接近于最优采样。 - 其次考虑p2,采样p2数据的可能性出现在B中的概率更大,权重

 接近于1,但是毕竟函数值很小,所以贡献也很小。
接近于1,但是毕竟函数值很小,所以贡献也很小。
然而有两个效果会带来大的方差:
从样本p1抽样得到的值可能是在AB的边界附近,![]() 明显小于1,因此样本贡献就比最优采样的
明显小于1,因此样本贡献就比最优采样的![]() 小了很多,显示在积分值的效果上就是暗了一些:
小了很多,显示在积分值的效果上就是暗了一些:
 这里面的小黑点就是这么来的。
这里面的小黑点就是这么来的。
另外就是p2的样本可能发生在区域A,这个时候![]() 很小,但是贡献:
很小,但是贡献:
![]()
确是接近于![]() ,因为有可能从p1的样本也发生在区域A中,所以两者的估计值加起来就几乎是两倍的
,因为有可能从p1的样本也发生在区域A中,所以两者的估计值加起来就几乎是两倍的![]() ,所以就比正常结果亮了一倍,上图的比较亮的点也是这么来的。
,所以就比正常结果亮了一倍,上图的比较亮的点也是这么来的。
最终可知,额外引入的噪声来自于两个地方:
- 有些从p1采样得到的样本权重小于1:发生在区域AB边界附近,p1和p2大小相似。
- 一些从p2得到的样本占据了比较大的贡献。
很多样本因为在区域A中所以权重比较小,甚至有的样本在AB边界附近。(值得注意的是在p2>>p1的地方,权重![]() 可以忽略)。
可以忽略)。
我们完全可以依靠多次采样来获得更好的效果,但是,如果能在较少采样次数时就得到更好的优化结果,岂不是更好吗。
更好的策略
其实就是让更大的权重函数更接近1,让小的权重函数更接近0。这对减少上面的两种方差都有很大好处。
我们看上面的图,首先p1采样大部分都发生在区域A中,p1>p2,我们希望最优权重这个时候是1.
平衡启发的样本权重是 ![]() 大于1/2,我们通过让该权重变得更尖锐(大的更大,小的更小)来优化策略。例如,当权重大于1/2的时候,就设置为1。该方法可以减少从p2采样到区域A中的方差,因为这个时候平衡启发计算的权重
大于1/2,我们通过让该权重变得更尖锐(大的更大,小的更小)来优化策略。例如,当权重大于1/2的时候,就设置为1。该方法可以减少从p2采样到区域A中的方差,因为这个时候平衡启发计算的权重![]() ,所以就归0了。
,所以就归0了。
我们一共实现两种锐化策略,一种叫 截断启发(cutoff heuristic),一种叫幂启发(power heuristic)。
为了方便表示,令![]() ,平衡启发式就可以写为:
,平衡启发式就可以写为:
 ,就是红圈里的部分:
,就是红圈里的部分:
- 截断启发
设置一个阈值![]() ,丢掉小于阈值的权重:
,丢掉小于阈值的权重:
 ,其中
,其中 ![]() 。
。
- 幂启发
 经过实验发现β为2的时候比较理想。
经过实验发现β为2的时候比较理想。
样本的贡献![]() 与pi成比例,当 pi 相对于其他pk减小的时候,样本的贡献也在减小。(与平衡启发不同,平衡启发里无论是哪种采样技术产生的,它的贡献都是一样大的):
与pi成比例,当 pi 相对于其他pk减小的时候,样本的贡献也在减小。(与平衡启发不同,平衡启发里无论是哪种采样技术产生的,它的贡献都是一样大的):
我还是用上面两个采样技术各采样一次的例子来说明:

假如用采样技术p1采样,这个时候假如是平衡启发,则估值为 f/(p1+p2) :


但是幂启发就是 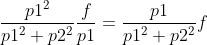 ,
,

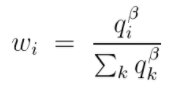
但是我觉得,它对于下面一种情况来说,效果会更坏:我们画个图来说明,蓝色表示被积函数,绿色表示p1采样的PDF,紫色表示p2采样的PDF:
 我们还是只用每个采样器分别采样一次
我们还是只用每个采样器分别采样一次
当用p1采样到下图红色区域的时候:根据f1/p1是最优采样,这个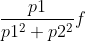 的效果甚至比
的效果甚至比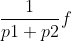 的估值还要差。
的估值还要差。

而当p1采样到如下红色区域时,幂启发式得到的估值确实比平衡启发式的效果要好。p2采样到红色区域的时候范围的时候估值也比平衡启发式的效果要好(f 的贡献变小了)。

其实平衡启发就是幂启发取 β=0 的结果。
- 最大启发
令幂启发的 β 为无穷大,可以得到:
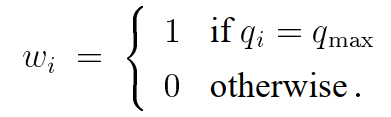
pi 产生的样本仅仅在区域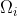 里权重为1。因为过多的样本被丢弃了,所以在实际当中效果不是很好,但是它给出了组合策略一些比较深层次的理解,而且很简洁。
里权重为1。因为过多的样本被丢弃了,所以在实际当中效果不是很好,但是它给出了组合策略一些比较深层次的理解,而且很简洁。
方差范围

F 是任意一种采样器,F' 是上面提到的各种启发式策略,c是常量:

单采样模型
随机从某一个采样技术中选择一个进行采样,只采样一个值。需要通过考虑权重如何计算来最小化其方差,在这个条件下,平衡启发式是最好的算法,方差最小。
给定 n 个采样技术,每个采样技术被选择的概率为c1,c2,c3……,然后采样到一个样本,这种方法在图形学中应用还比较广泛,因为BSDF可能会根据不同的glossy,diffuse或者specular选择。
 其中
其中![]() 表示根据 ci 随机分布的概率
表示根据 ci 随机分布的概率
估计器在上面讨论过的权重 wi 下是无偏的。
应该怎么选择权重wi来最小化方差呢?
设F是任何无偏估计器,![]() 是使用平衡启发式权重的估计器,经过论证,
是使用平衡启发式权重的估计器,经过论证,
![]()










 本文深入探讨了多重重要性采样(MIS)技术在光线追踪中的应用,对比分析了采样光源与采样BRDF的方法,并详细介绍了MIS的原理、多采样模型及其优势。此外,还讲解了几种权重函数的使用方法,包括balanceheuristic,以及如何通过实验验证理论的有效性。
本文深入探讨了多重重要性采样(MIS)技术在光线追踪中的应用,对比分析了采样光源与采样BRDF的方法,并详细介绍了MIS的原理、多采样模型及其优势。此外,还讲解了几种权重函数的使用方法,包括balanceheuristic,以及如何通过实验验证理论的有效性。


















 1063
1063

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










