周志华-机器学习-笔记（五）- 强化学习

 #### 任务与奖赏 ####

　　“强化学习”(reinforcement learning)可以讲述为在任务过程中不断摸索，然后总结出较好的完成任务策略。
　　强化学习任务通常用马尔可夫决策过程(Markov Decision Process，简称MDP)来描述：机器处于环境$E$中，状态空间为$X$，其中每个状态$x \in X$是机器感知到的环境的描述；机器能采取的动作构成了动作空间$A$；若某个动作$a \in A$作用在当前状态$x$上，则潜在的转移函数$P$将使得环境从当前状态按某种概率转移到另一个状态；在转移到另一个状态的同时，环境会根据潜在的“奖赏”(reward)函数$R$反馈给机器一个奖赏；综合起来，强化学习任务对应了四元组$E=<X,A,P,R>$，其中$P:X \times A \times X \rightarrow \mathbb{R}$指定了状态转移概率，$R:X \times A \times X \rightarrow \mathbb{R}$指定了奖赏；在有的应用中，奖赏函数可能仅与状态转移有关，即$R:X \times X \rightarrow \mathbb{R}$。

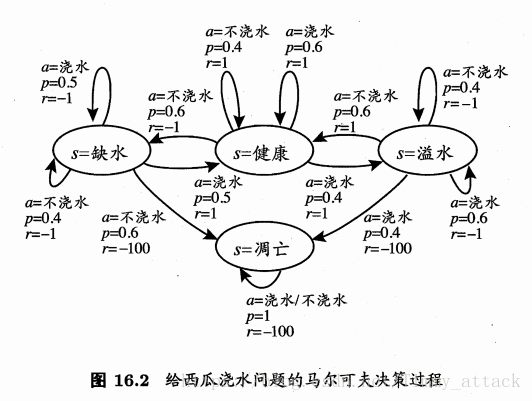
　　图16.2给出了西瓜浇水的马尔可夫决策过程。该任务中只有四个状态（健康、缺水、溢水、凋亡）和两个动作（浇水、不浇水），在每一步转移后，若状态是保持瓜苗健康则获得奖赏$1$，瓜苗缺水或溢水奖赏为$-1$，当瓜苗凋亡时奖赏是最小值$-100$。箭头代表状态转移，箭头旁的$a,p,r$分别代表导致状态转移的动作、转移概率以及返回的奖赏。
　　机器要做的是通过在环境中不断地尝试而学得一个“策略”(policy)$\pi$，根据这个策略，在状态$x$下就能得知要执行的动作$a=\pi(x)$。策略有两种表示方法：一种是将策略表示为函数$\pi:X \rightarrow A$，确定性策略常用这种表示；另一种是概率表示$\pi:X \times A \rightarrow \mathbb{R}$，随机性策略常用这种表示，$\pi(x,a)$为状态$x$下选择动作$a$的概率，这里必须有$\sum_a \pi(x,a)=1$。
　　策略的优劣取决于长期执行这一策略后得到的累积奖赏。在强化学习任务中，学习的目的就是要找到能使长期积累奖赏最大化的策略。长期积累奖赏有多种计算方式，常用的有“T步积累奖赏”$\mathbb{E}[\frac{1}{T} \sum^{T}_{t=1}r_t]$和“r折扣累积奖赏”$\mathbb{E}[\sum^{+\infty}_{t=0}\gamma^{t}r_{t+1}]$，其中$r_t$表示第$t$不获得的奖赏值，$\mathbb{E}$表示对所有随机变量求期望。

K-摇臂赌博机

探索与利用

　　我们考虑比较简单的情形：最大化单步奖赏，即仅考虑一步操作。这时需要考虑两个方面：一是需知道每个动作带来的奖赏，二是要执行奖赏最大的动作。
　　单步强化学习任务对应了一个理论模型，即“K-摇臂赌博机”(K-armed bandit)。

　　K-摇臂赌博机和我们常见的老虎机差不多，投入硬币后可选择按下其中一个摇臂，每个摇臂以一定的概率吐出硬币。
　　若仅为获知每个摇臂的期望奖赏，则可采用“仅探索”(exploration-only)法：将所有的尝试机会平均分配给每个摇臂（即轮流按下每个摇臂），最后以每个摇臂各自的平均吐币概率作为其奖赏期望的近似估计。
　　若仅为执行奖赏最大的动作，则可采用“仅利用”(exploitation-only)法：按下目前最优的（即到目前为止平均奖赏最大）的摇臂，若有多个摇臂同为最优，则随机选择其中一个。
　　显然，“仅探索”法能很好地估计每个摇臂的奖赏，却会市区很多选择最优摇臂的机会；“仅利用”法则相反，它没有很好地估计摇臂期望奖赏，很有可能经常选不到最优摇臂。因此，这两种方法都难以使得最终的积累奖赏最大化。
　　由于尝试次数是有限的，“探索”和“利用”这两者相互矛盾，加强了一方则会自然消弱另一方，这就是强化学习所面临的“探索-利用窘境”(Exploration-Exploitation dilemma)。欲使积累奖赏最大，则必须在探索与利用之间达成较好的折中。

$\epsilon$-贪心

　　$\epsilon$-贪心法基于一个概率来对探索和利用进行折中：每次尝试时，以$\epsilon$的概率进行探索，即以均匀概率随机选取一个摇臂；以$1-\epsilon$的概率进行利用，即选择当前平均奖赏最高的摇臂（若有多个，则随机选取一个）。
　　令$Q(k)$记录摇臂$k$的平均奖赏，若摇臂$k$被尝试了$n$次，得到的奖赏为$v_1,v_2,...,v_n$。一般，我们对均值进行增量式计算，即每尝试一次就立即更新Q(k)。这样每次尝试仅需记录两个值：已尝试次数$n-1$和最近平均奖赏$Q_{n-1}(k)$

$$Q_n(k) = Q_{n-1}(k) + \frac{1}{n}(v_n - Q_{n-1}(k)) \tag{16.3}$$
　　 $\epsilon$-贪心算法描述如图16.4所示

$Q(i)$和 $count(i)$分别记录摇臂 $i$的平均奖赏和选中次数。
　　若摇臂奖赏的不确定性较大，例如概率分布较宽时，则需更多的探索，此时需要较大的$\epsilon$值；若摇臂的不确定性较小，例如概率分布较集中时，则小量的尝试就能很好地近似真实奖赏，此时需要的 $\epsilon$较小。

Softmax

　　Softmax算法基于当前已知的摇臂平均奖赏来对探索和利用进行折中。若各个摇臂的平均奖赏相当，则选取各摇臂的概率也相当；若某些摇臂的平均奖赏明显高于其他摇臂，则被选取的概率也明显更高。
　　Softmax算法中摇臂概率的分配是基于Boltzmann分布：

$$P(k) = \frac{e^{\frac{Q(k)}{\tau}}}{\sum_{i=1}^{K}e^{\frac{Q(i)}{\tau}}} \tag{16.4}$$ 其中， $Q(i)$记录当前摇臂的平均奖赏； $\tau > 0$称为“温度”， $\tau$越小则平均奖赏高的摇臂被选择的概率越高。 $\tau$趋于 $0$时Softmax将趋于“仅利用”，$\tau$趋于无穷大时Softmax则趋于“仅探索”。

有模型学习

　　假定任务对应的马尔可夫决策过程四元组$E=<X,A,P,R>$均为已知，这样的情形称为“模型已知”，即机器对环境进行了建模。

策略评估

　　在模型已知时，对任意策略$\pi$能估计出该策略带来的期望积累奖赏。令函数$V^{\pi}(x)$表示从状态$x$出发，使用策略$\pi$所带来的积累奖赏；函数$Q^{\pi}(x,a)$表示从状态$x$出发，执行动作$a$后再使用策略$\pi$带来的积累奖赏。这里$V(\cdot)$称为“状态值函数”(state value function)，$Q(\cdot)$称为“状态-动作值函数”(state-action value function)，分别代表指定“状态”上以及指定“状态-动作”上的积累奖赏。可以定义状态值函数

$$\begin{cases} V^{\pi}_{T}(x) = \mathbb{E}_{\pi}[\frac{1}{T}\sum^{T}_{t=1}r_t \;|\; x_0 = x]， T步积累奖赏； \\ V^{\pi}_{\gamma}(x) = \mathbb{E}_{\pi}[\sum^{+\infty}_{t=0}\gamma^{t}r_{t+1} \;|\; x_0 = x]，\gamma折扣积累奖赏 \end{cases} \tag{16.5}$$
　　令 $x_0$表示起始状态， $a_0$表示起始状态上采取的第一个动作；对于 $T$不积累奖赏，用下标$t$表示后续执行的步数。有状态-动作值函数
$$\begin{cases} Q^{\pi}_{T}(x,a) = \mathbb{E}_{\pi}[\frac{1}{T}\sum^{T}_{t=1}r_t \;|\; x_0 = x,a_0 = a]; \\ Q^{\pi}_{\gamma}(x,a) = \mathbb{E}_{\pi}[\sum^{+\infty}_{t=0}\gamma^{t}r_{t+1} \;|\; x_0 = x,a_0 = a]. \end{cases} \tag{16.6}$$