[Contrastive Learning] Improving Contrastive Learning by Visualizing Feature Transformation

[Contrastive Learning] Improving Contrastive Learning by Visualizing Feature Transformation

• 论文链接：Arxiv
• 期刊/会议：ICCV 2021 Oral
• 是否有code: Code

关键词

对比学习 可视化方法 数据增广

问题简述

Motiviation

这是篇卖“方法”的文章。

• 作者提供了一种可视化工具(称之为score distribution)，来分析、解释与理解对比学习的学习过程
• 基于score distribution的观察，作者提出了两种特征层面上的增广方式(Feature Transformation, FT)，能够有效涨点。FT的使用十分方便，能够嵌入到各类对比学习方法之中；

方法介绍

先借用文章中的一图一公式来简单回顾下主流对比学习范式

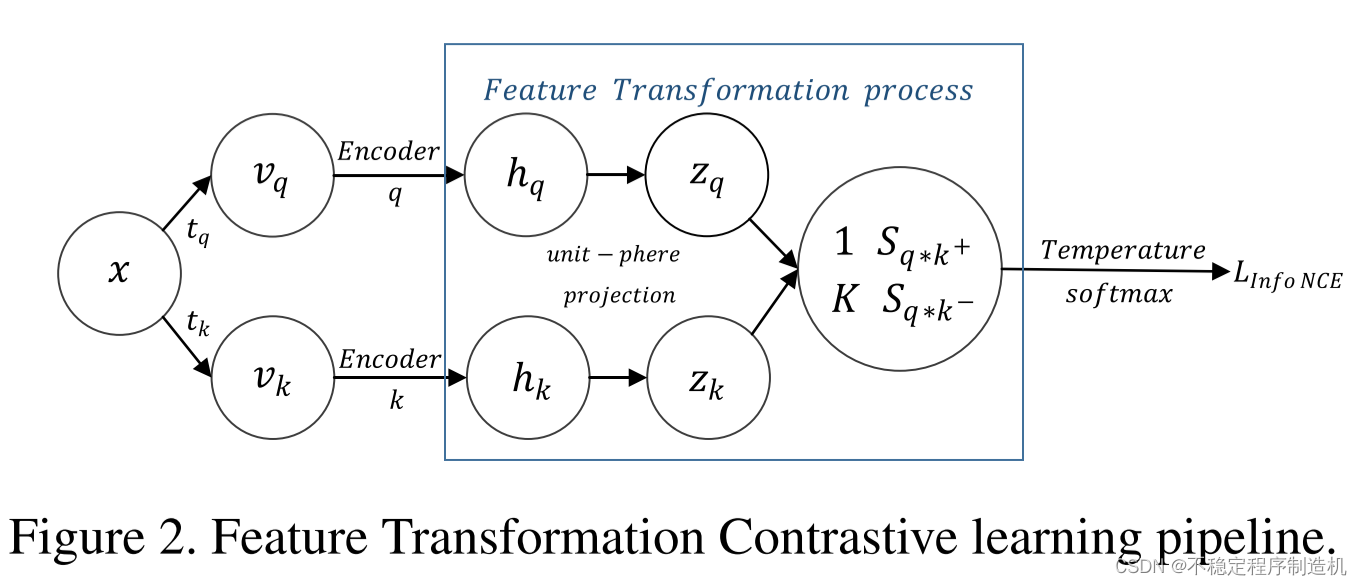
$${\mathcal{L}}_{\mathcal{I}nfo\text{NCE}}=-log[\frac{exp(S_{q\cdot k^{+}}/\tau )}{exp(S_{q\cdot k^{+}}/\tau )+{\sum }_{K}exp(S_{q\cdot k^{-}}/\tau )}]\text{\hspace{1em}(1)}$$

可视化工具 Score Distribution Visualization：

什么是Score Distribution呢？其实就是指$S_{q\cdot k^{+}}$（positive score distribution）与$S_{q\cdot k^{-}}$ （negative score distribution），就是这么简单。
那为什么要使用score distribution呢？作者解释了两点：

• 主流的对比学习范式都是用InfoNCE损失，而InfoNCE损失其实就是在比较经过log-softmax之后的positive/negative score distributions。因此，使用score distribution能够更加直观的反应InfoNCE损失的学习过程；
• $S_{q\cdot k^{+}}$ 和 $S_{q\cdot k^{-}}$ 是标量，数据量少，便于存储和可视化；

那Score Distribution怎么反应对比学习过程学的好坏呢？作者基于score distribution提出了三个统计量：

1. positive score distribution均值，以下简称为$mea{n}_{psd}$.
2. negative score distribution均值，以下简称为$mea{n}_{nsd}$.
3. negative score distribution方差，以下简称为$va{r}_{nsd}$.

以这三个统计量为基础，作者提出了两个标准：

• 在学习过程中，$mea{n}_{psd}$最好不要太高。太高，说明参与训练的正例都是简单例，阻碍网络学习到更“本质”的特征；
• 在学习过程中，$va{r}_{nsd}$最好不要太大，即$mea{n}_{nsd}$的曲线最好保持平滑与稳定。波动太剧烈说明学习过程不稳定，容易导致模型塌缩(model collapse);

如何验证这两条标准是合理的呢，作者通过在MOCO中引入Score Distribution可视化工具来通过模型性能反推可视化工具的有效型，看下图：

从上图（a）中我们可以看到，MOCO的效果随着动量参数m的变化而变化。用橙色曲线表示的$m=0.99$分类精度达到56.2，是最好的； 蓝色曲线代表的$m=0.999$次之，达到53.1；而绿色曲线代表的$m=0.9$则只有46.5，模型性能大幅下降，塌缩了。
对比三种曲线在(a),(b),©三张子图上的表现，发现橙色曲线的表现是最符合两条标准的，即：

• （a）图中，橙色曲线最小，代表$va{r}_{nsd}$最小，蓝色和绿色依次变大，最终模型的分类精度也依次下降；
• （b）图中，绿色曲线最不平滑，即$mea{n}_{nsd}$波动较大，反映了$m=0.9$时模型塌缩了；
• （c）图中，绿色曲线的$mea{n}_{psd}$最高，效果也最差，暗合标准1。

emmm，多少感觉有点牵强，不过看在Score Distribution是第一种分析对比学习的可视化工具，忍了。

特征层面数据增广 Feature Transformation：

本文提出了两种FT方式：

1. positive pair extrapolation，正例外延。目的是把正例之间的距离拉远，从而提升$mea{n}_{psd}$；
   做法如下：
   $$\begin{gathered} {\hat{z}}_q={\lambda }_{ex}{z}_q+(1-{\lambda }_{ex})z_{k^{+}} \\ {\hat{z}}_{k^{+}}={\lambda }_{ex}{z}_{k^{+}}+(1-{\lambda }_{ex})z_q \end{gathered}$$
   ${\lambda }_{ex}$是超参数，要求大于1，满足Beta分布 $\lambda \sim Beta({\alpha }_{ex},{\alpha }_{ex})+1$, 实验证明$({\alpha }_{ex}>1$效果会比较好；其原理就和上图(b)中类似，这种做法实现简单的同时，能够满足$S_{q\cdot k}\ge {\hat{S}}_{q\cdot k}$

2. negative pair interpolation，负例插值。目的是提升负例之间的多样性，从而提升$mea{n}_{psd}$；
   $${\hat{Z}}_{neg}={\lambda }_{in}\cdot Z_{neg}+(1-{\lambda }_{in})\cdot Z_{perm}$$
   $Z_{neg}$就是负例的集合，在MOCO中就是memory queue，在SimCLR中就是BatchSize中的所有负例。假设 Z n e g = { z 1 , z 2 , . . . , z K } Z_{neg}=\{z_{1},z_{2},...,z_{K}\} Zneg​={z1​,z2​,...,zK​}$Z_{perm}$中的perm是permutation的缩写，即将$Z_{neg}$这个序列的顺序打乱。同样的，${\lambda }_{in}$是超参数，同样也从Beta分布中采样得到 $\lambda \sim Beta({\alpha }_{in},{\alpha }_{in})$。
   原文中对于负例插值的作用解释如下：在负例数量不多的前提下，由负例构成的空间是十分稀疏的，通过负例(内)插值，能够使这个系数的空间更"稠密"一些，降低波动的影响；

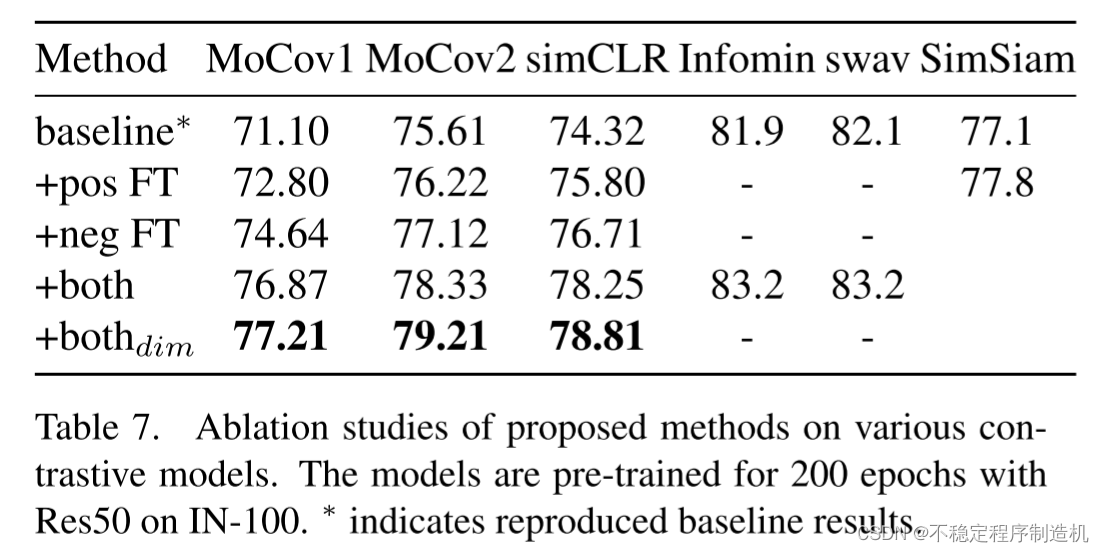
可以看出，两种FT效果还是挺明显的，而且对于对比学习框架没有约束，各个方法都能用。相比之下负例内插的效果更明显些，也符合“增大K值”很重要的一个共识。上表中最后一行代表着超参${\lambda }_{ex}$与${\lambda }_{in}$从一个标量变为了向量，两个FT操作也随之由vector-level变成了dimension-level；

在不同的数据集上，效果也很好；

总结

卖方法的，思路不是很新颖，不过优点很明显：

1. 能自圆其说，由Score Distribution的发现引入Feature Transformation的过程很自然。
2. 效果很强，同时实现简单；
   缺点：
3. 把Score Distribution作为一款可视化分析工具来说，感觉有点微妙。文中仅以MOCO的三个实验的纵向对比为例，不知道能否在不同的方法中进行横向对比？

顺道一提，本文有附加支撑材料，这个博文中没有涉及，读者有兴趣可以去看看。

参考文献

本文基本均为原创

Over~收工。