排序算法（1）——插入排序

插入排序（Insertion Sort）

    （1）算法思想

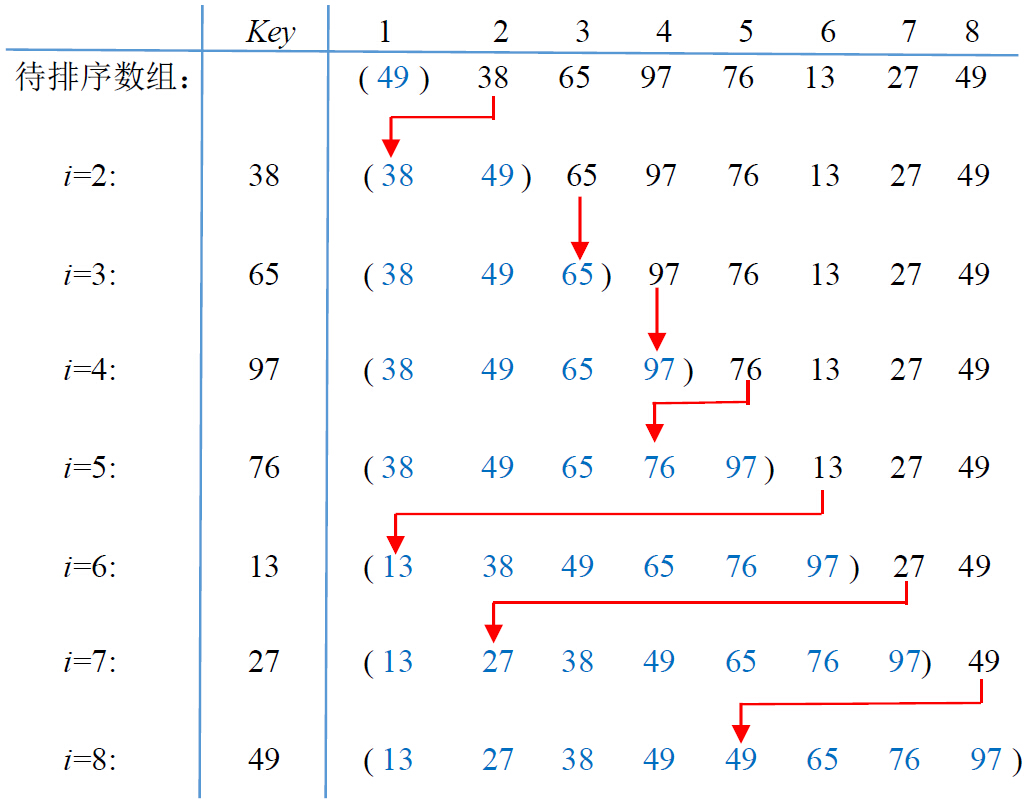
              插入排序的思想非常简单，给定待排序的数组A[1..n]，依次对数组A的第2个到第n个元素执行插入操作。当对第j个元素（称为关键字，key）进行插入操作时，假设A[1..j-1]已经是有序序列了（前面元素的插入操作已经使之有序），则只需在A[1..j-1]中从后往前搜索，找到第一个小于等于A[j]的元素，将A[j]插入到这个元素后面即可。具体排序过程如下图所示：

    （2）伪代码

             INSERTION-SORT(A)
             1 for j ← 2 to length(A)                   // length(A)表示数组A的元素个数，即n
             2      do key ← A[j]                          // 接下来将A[j]插入到已排序的序列A[1..j-1]中
             3           i ← j – 1                              // 从j的前一个元素开始从后往前进行搜索
             4          while i > 0 and A[i] > key
             5                    do A[i+1] ← A[i]      // 遇到大于A[j]的元素往后移动，遇到小于等于A[j]的元素停止搜索
             6                         i ← i – 1
             7           A[i+1] ← key                     // 找到插入位置

    （3）代码实现

              注意：具体实现的时候，数组下标是从0开始，这里跟伪代码中有一点区别。            

void InsertionSort(int A[],int n)
{
    int j;
    for(j=1;j<n;j++)
    {
        int key=A[j];
        int i=j-1;
        while(i>=0&&A[i]>key)
        {
            A[i+1]=A[i];
            i--;
        }
        A[i+1]=key;
    }
}

          另外，插入排序也可以用递归实现，首先对A[1..n-1】进行递归排序，然后将A[n]插入到已经排好序的A[1..n-1]中，具体实现如下：

void InsertionSort(int A[],int n)
{
    if(n>0)
    {
        InsertionSort(A,n-1);
        int i=n-2;
        int key=A[n-1];
        while(i>=0&&A[i]>key)
        {
            A[i+1]=A[i];
            i--;
        }
        A[i+1]=key;
    }

（4）算法分析

             a.运行时间分析：  插入排序时间开销与输入序列的规模（即待排序数组的长度）及数组的已排序程度有关。输入序列规模越大，时间开销越大；相同规模的两个序列，已排序程度越小，时间开销越大。算法时间开销的最佳情况出现在输入序列为已排序序列时，最坏情况出现在输入序列为逆序排列序列时。

             b.时间复杂度：Θ(n^2)（注：时间复杂度一般考察算法的最坏情况时的时间代价）。

             c.插入排序是原地排序（sort in place），即在待排序的数组内部进行排序，不需要额外申请新的空间作临时容器。

             d.插入排序是稳定排序（stable sort），所谓稳定排序是指待排序序列中有两个（或者两个以上）相等的元素：Ai=Aj，排序前i<j，若排序后仍然满足i<j，即相等元素排序前后的顺序并未改变，则称这种排序算法是稳定的。

             e.若数据用的是双向链表这种数据结构来存储，要实现对这个双向链表的排序，使用插入排序是一个不错的选择，因为链表这种数据结构若选择需要频繁交换的排序算法（如冒泡排序），代价极大。