本文介绍了图论的基础概念，包括有向图和无向图的定义，强调了边的方向和邻接关系。在有向图中，边由一对有序顶点表示，而在无向图中，边是无方向的。还讨论了顶点的度（入度和出度），以及路径的概念，包括可达性和简单路径。
图论基础(一)
有向图定义
有向图G是一个二元组(V, E)，记为G=(V, E)。
其中V是有向图G的顶点集合，是一个有限集合，元素为顶点；E是有向图G的边集合，元素为边，边也是一个二元组< u, v >，其中u，v是有向图G的顶点集合中的元素，< u, v >在这里是有方向的边，以u为起点，指向v的一条有向路径。u可以与v相同，代表自身指向自身的一个自环路径。
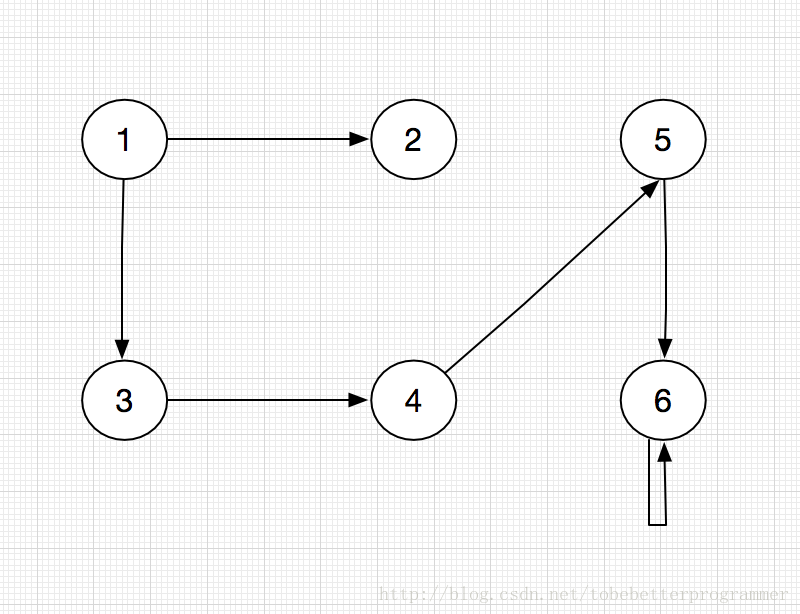
假定存在有向图G=(V, E)，顶点集合V={ 1, 2, 3, 4, 5, 6 }，边集合E={ < 1, 2 >, <1, 3>, < 3, 4 >, < 4, 5 >, < 5, 6 > , < 6, 6 > } ，该有向图的结构则为以下形式：
最低0.47元/天 解锁文章
扫一扫
5505
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
