无刷直流发电机高效电能转换

电气工程

无刷直流发电机用低成本电能转换系统 最大化的设计与实现

阿博尔法兹勒·哈尔瓦伊·尼亚萨尔*，阿米尔侯赛因·萨巴格安
Faculty卡尚大学电气与计算机工程学院，伊朗卡尚，邮政信箱：87317‐51167
2015年8月30日收到；2015年10月22日修订；2015年11月1日接受

关键词 无刷直流发电机；永磁同步发电机；功率密度最大化；有源整流器；电流整形

摘要

本文提出了一种简单且低成本的方法，用于捕获永磁无刷直流（BLDC）发电机的最大功率输出。传统的整流方法基于无源变换器，由于无法将电流波形控制为理想波形，导致从无刷发电机中抽取高度畸变的电流。这会降低功率因数，并减小效率和每安培功率能力。因此，在本研究中采用了一种有源六开关功率变换器，并根据相位反电动势电压生成最优电流波形。相电流被控制为与相电压同相，其幅值被调节以稳定直流母线电压。所提出的控制理论通过针对无刷直流电机（BLDC）发电机和永磁同步发电机（PMSG）的仿真得到了验证。此外，还提供了一些实验结果，以证明理论分析和仿真结果的正确性。

2015艾因夏姆斯大学工程学院。由Elsevier出版和托管。这是一篇根据知识共享署名‐非商业性‐禁止演绎许可（http://creativecommons.org/licenses/by-nc-nd/4.0/）发布的开放获取文章。

引言

如今，分布式发电系统以及电动汽车和混合动力汽车推进系统的发展显著提升了永磁（PM）无刷发电机的普及程度。这类发电机已广泛应用于汽车等领域，微型涡轮机、风力发电，因其高功率密度、鲁棒性和可靠性 [1]。永磁无刷发电机主要有两种类型：梯形波型（BLDCG）和正弦波型（PMSG）。若采用现代基于矢量的控制技术，PMSG需要高分辨率位置传感器才能实现最佳运行，而BLDCG仅需三个低成本的霍尔效应位置传感器[2]。与其他发电机相比，无刷直流电机具有重量轻、紧凑设计、控制简便和低维护等优点[3,4]。与永磁同步发电机相比，无刷直流发电机的功率密度可高出约15%[5]。

另一方面，由于在许多独立发电系统（如风能转换系统（WECS）或汽车应用）中，发电机转轴的变速导致输出电压频率变化，因此需要配备电力电子接口以连接到永磁无刷发电机。该系统中最关键的问题是在较低损耗下从发电机中提取最大电能，从而减小发电机的尺寸和重量[6]。

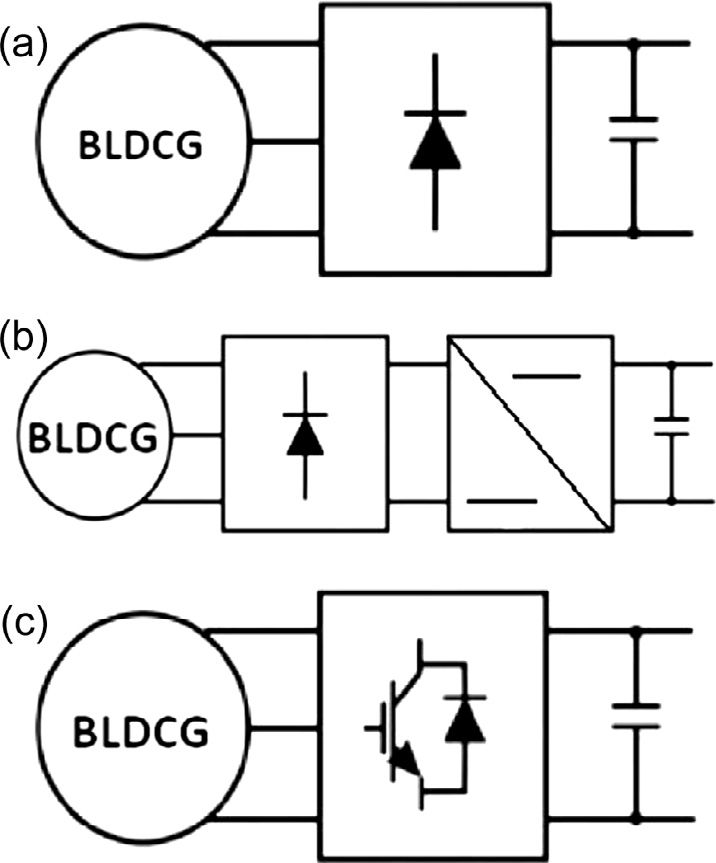
图1显示了无刷直流发电系统所采用的各种拓扑结构。

最简单的解决方案是使用如图1(a)所示的不可控三相整流器，该方案无需任何控制且成本最低。在这种情况下，发电机的反电动势幅值必须高于直流母线电容电压，而该电压会因取决于发电机转速和直流负载而发生变化。因此，输出功率取决于转速和负载电阻。因此，采用不可控整流器的拓扑结构具有相对较低的效率和较低的功率密度[7]。

由于上述缺点，在某些应用中，无刷直流发电机通过二极管桥与DC/DC变换器拓扑结构进行控制，如图1(b)所示。通过在任何无刷直流发电机上增加二极管桥，可以采用不同的DC/DC变换器，并实现对电压、电流或功率的调节。其主要原因在于利用该解决方案的原因在于其简单性和模块化设计。然而，这种拓扑结构的主要缺点之一是交流侧出现严重畸变的不可控电流，导致每安培低功率。在这种拓扑结构中，无刷直流发电机的相电压和电流不同相，因此功率因数降低 [8]。

另一种解决方案是使用带有六个有源开关的功率变换器，如图1(c)[9,10]所示。对于该拓扑结构，可以采用多种控制策略，例如基于矢量、电流波形整形和电流优化策略。这似乎使得变速发电机的控制硬件变得复杂且昂贵，但在驱动器的低轴转速下表现出色。这种复杂系统可见于电动汽车和混合动力汽车的再生制动应用中。通过这种方式，可以从无刷直流发电机中提取每安培最大功率[11]。

直接功率控制策略已被用于无刷直流发电机系统的电压和功率调节[12]。在[13]中提出了一种电流控制方法，以消除转矩脉动并最大化非正弦无刷直流电机在电动汽车和混合动力电动汽车中的功率密度。为此，针对特定谐波的消除采用了简单的代数方法而非快速傅里叶变换。文献[14]提出了一种基于同时最小化转矩脉动和焦耳损耗的无刷直流发电机预测控制方法。在[15]中，采用了一种固定转子转速下的混合永磁（HPM）发电机和无源滤波器，为混合动力电动汽车产生可变直流母线电压。通过控制电机励磁来获取期望的功率和电压。前述由电流畸变引起的问题已通过复杂系统得以解决。

另一种基于无刷直流发电机的供电系统在[16]中被用于小型风能转换系统，其中采用DC/DC变换器进行直流母线电压调节。在[17]中，采用了一种基于无刷直流发电机的风能转换系统用于分布式发电，使用PWM整流器控制无刷直流发电机的功率，且参考相电流为矩形波。

本文提出了一种用于无刷直流发电机的新型电流成形算法的分析与实现。所开发的算法可设计用于最大功率提取或直流电压调节。该系统可用于风能转换系统、汽车系统中的再生制动以及基于微型涡轮的供电系统。在描述之后

符号说明

• ea, eb, ec：定子相位反电动势电压
• H1; H2; H3：霍尔效应位置传感器的输出信号
• ia; ib; ic：定子相电流
• I0 a：负斜率部分参考相电流
• Ls：每相定子电感
• M：定子互感
• Pavg：平均气隙功率
• Poutput：发电机输出功率
• Rs：每相定子电阻
• tH1;off：传感器 H1 的下降沿时刻
• tH1;on：传感器 H1 的上升沿时刻
• tH2;off：传感器 H2 的下降沿时刻
• tH2；开启：传感器H2的上升沿时刻
• va；vb；vc：定子端电压
• BLDCG：无刷直流发电机
• EV：电动汽车
• EMF：电动势
• FFT：快速傅里叶变换
• HEV：混合动力电动汽车
• PM：永磁体
• PMDC：永磁直流
• PMSG：永磁同步发电机
• WECS：风能转换系统

2. 无刷直流发电机的最优功率控制

2.1. 无刷直流发电机系统及建模

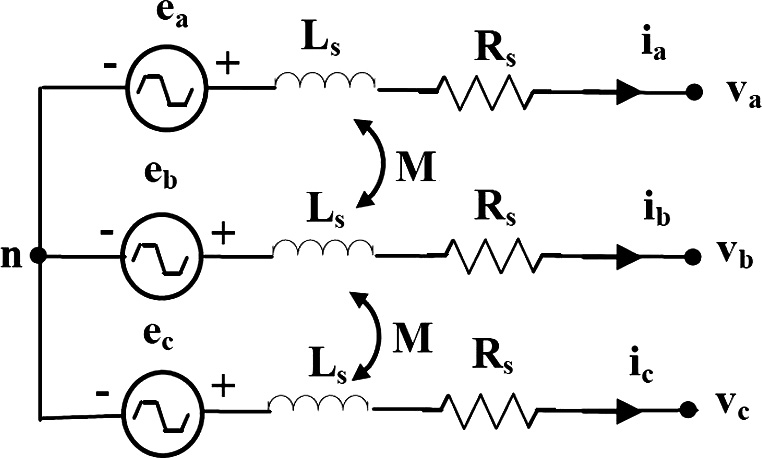
为了简化三相控制并最大化输出功率，推导了无刷直流发电机的等效动态模型。无刷直流发电机的等效电路如图2所示。假设三绕组各相的电阻和电感相等，感应相反电动势电压具有相同的波形；开关和铁损可忽略不计[5]。基于这些假设，无刷直流发电机的相电压方程可表示如下：

$$
\begin{bmatrix}
e_a \
e_b \
e_c
\end{bmatrix}
=
\begin{bmatrix}
R_s & 0 & 0 \
0 & R_s & 0 \
0 & 0 & R_s
\end{bmatrix}
\begin{bmatrix}
i_a \
i_b \
i_c
\end{bmatrix}
+
\begin{bmatrix}
L_s - M & 0 & 0 \
0 & L_s - M & 0 \
0 & 0 & L_s - M
\end{bmatrix}
\frac{d}{dt}
\begin{bmatrix}
i_a \
i_b \
i_c
\end{bmatrix}
+
\begin{bmatrix}
v_a \
v_b \
v_c
\end{bmatrix}
\quad (1)
$$

其中，ex、vx、ix、Rs、Ls和M分别表示相位反电动势电压、端电压、相电流、相电阻、相自感和互感。

无刷直流发电机产生具有梯形波形的三相反电动势，如图3所示，其幅值与转速成正比。无刷直流发电机的相电流波形取决于连接到发电机的功率转换电路及所采用的整流策略。为了最大化无刷直流发电机的输出功率，将提出一种最优电流控制策略。

2.2. 无刷直流发电机的功率

在三相无刷直流发电机中，平均气隙功率由以下公式得到：

$$
P_{avg} = \sum_{k=a,b,c} \frac{1}{T} \int_0^T e_k(t)i_k(t)dt
= \frac{1}{T} \int_0^T \left{ e_a(t)i_a(t) + e_b(t)i_b(t) + e_c(t)i_c(t) \right} dt
= \frac{3}{T} \int_0^T e_a(t)i_a(t)dt
\quad (2)
$$

其中 ek(t) 表示感应相反电动势电压，ik(t) 是发电机的相电流。

根据相电压方程 (1)，无刷直流电机发电机的输出功率由下式计算：

$$
P_{output} = \sum_{k=a,b,c} \frac{1}{T} \int_0^T v_k(t)i_k(t)dt
= \frac{3}{T} \int_0^T \left{ e_a(t) - R_s i_a(t) - L_s \frac{di_a(t)}{dt} \right} i_a(t) dt
= \frac{3}{T} \int_0^T e_a(t)i_a(t)dt - 3R_s i_{a,rms}^2 - \frac{3L_s}{T} \int_0^T i_a(t)\frac{di_a(t)}{dt}dt
$$

可以看出，气隙功率由三部分组成：输出功率、定子铜损和定子电感平均功率，其中后者为零。由于在特定有效值电流下铜损为恒定值，且电感分量的平均功率为零，因此为了最优利用输出功率，最大化策略可应用于气隙功率的组成部分。

2.3. 无刷直流发电机功率最大化的基本原理

无刷直流发电机的反电动势电压呈梯形，为了最大化气隙功率，应注入梯形相电流波形。这是由于气隙功率与相反电动势电压和电流的乘积相关。如果相电流和电压具有相同的形状，则电压和电流的所有谐波分量将产生功率。另一个要点是，相电压和电流应同相。因此，以下技术基于电流控制，呈梯形且与电压同相。这一原理同样适用于永磁同步发电机。因此，为了最大化永磁同步发电机的功率输出，由于定子绕组中感应电压为正弦波形，电流的最佳波形应为与电压同相的正弦波。

2.4. 参考电流波形生成

对于基于相电流控制成形的无刷直流发电机功率最大化，需要生成参考电流波形。为了进行比较，三种参考电流考虑了方波、正弦和梯形波形，并将其注入BLDCG的各相中。将产生最大功率的电流波形定义为最优电流。

为了使a相参考电流的梯形波形与电压同相，采用了一种基于霍尔效应位置传感器信号的新技术，而无需使用昂贵的轴编码器。参考电流的幅值根据所需功率确定，如(2)所示。在图3中，当A相反电动势电压（ea）的正平部分即将开始时，传感器状态为H1= 1 和H2= 0；当ea进入负平部分时，传感器状态变为H1= 0和 H2= 1。a相梯形参考电流的负斜率部分可由以下公式得出：

$$
I_{0a} = -\frac{2}{t_{H2,on} - t_{H1,off}} (t - t_{H2,on}) + 1 \quad (4)
$$

其中，$t_{H2,on}$ 和 $t_{H1,off}$ 分别是传感器H2的上升沿时刻和传感器 H1的下降沿时刻。以相同的方式，可推导出a相梯形参考电流的正斜率部分。因此，为了使整个梯形相参考电流与反电动势电压同相，可采用以下关系：

$$
\begin{cases}
\text{if } H1 = 1 \& H2 = 0 \Rightarrow I_{0a} = 1 \
\text{if } H1 = 1 \& H2 = 1 \Rightarrow I_{0a} = -\frac{2}{t_{H2,on}-t_{H1,off}}(t - t_{H2,on}) + 1 \
\text{if } H1 = 0 \& H2 = 1 \Rightarrow I_{0a} = -1 \
\text{if } H1 = 0 \& H2 = 0 \Rightarrow I_{0a} = \frac{2}{t_{H2,off} - t_{H1,on}} (t - t_{H2,off}) - 1
\end{cases}
\quad (5)
$$

类似的关系可以用来为B相和C相生成梯形参考电流。

3. 仿真结果

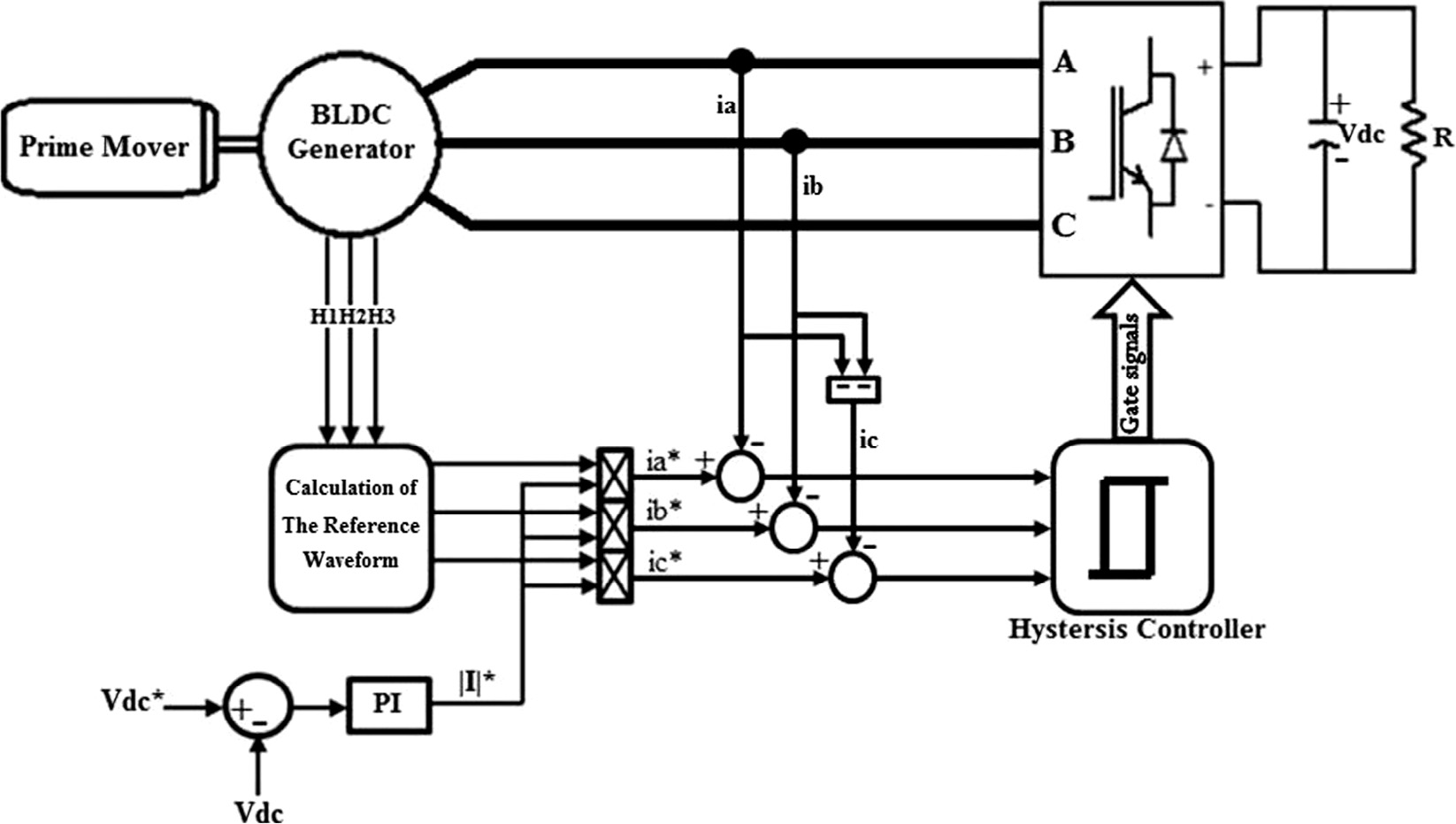
通过一些仿真验证了所提出的最大化输出功率的控制方法。图4显示了发电系统的拓扑结构。无刷发电机通过永磁直流电机作为原动机进行耦合，并连接到有源三相整流器，以将直流功率传递给直流母线和电阻负载。整流器被控制以捕获最大功率且不产生无功功率，并将直流母线电压维持在期望水平。

由于无刷发电机（梯形或正弦）的反电动势电压中，三相参考电流与反电动势电压同相位生成。采用三个滞环电流控制器产生施加于有源整流器的开关信号。如前所述，对于无刷直流发电机，使用霍尔效应位置传感器信号生成梯形参考电流，而对于永磁同步发电机，则需要轴编码器。对无刷直流发电机和永磁同步发电机均进行了仿真。

对于每台电机，比较了三种不同参考电流波形下的输出功率。这些情况包括：(a) 使用无源整流器，(b) 使用正弦电流参考的有源整流器，(c) 使用梯形电流参考的有源整流器。为了更便于比较，在相同转速、负载和定子有效值电流（或相同的定子铜耗和旋转损耗）条件下计算发电机的输出功率。

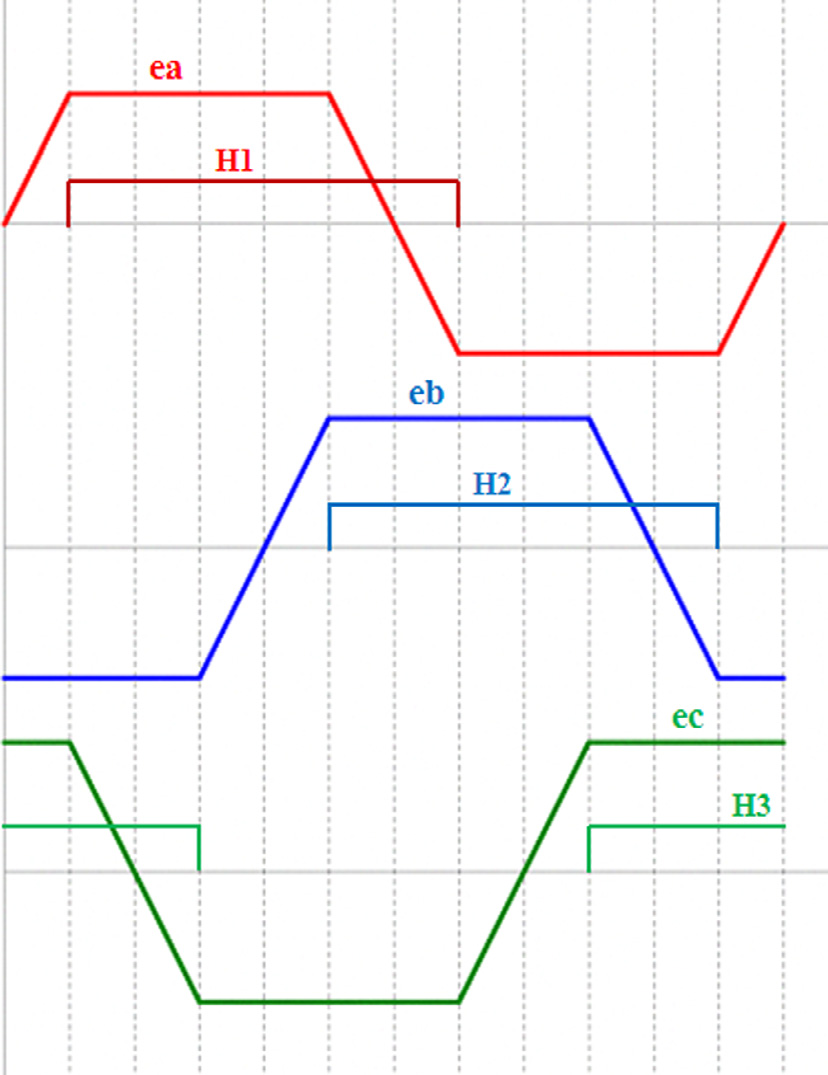
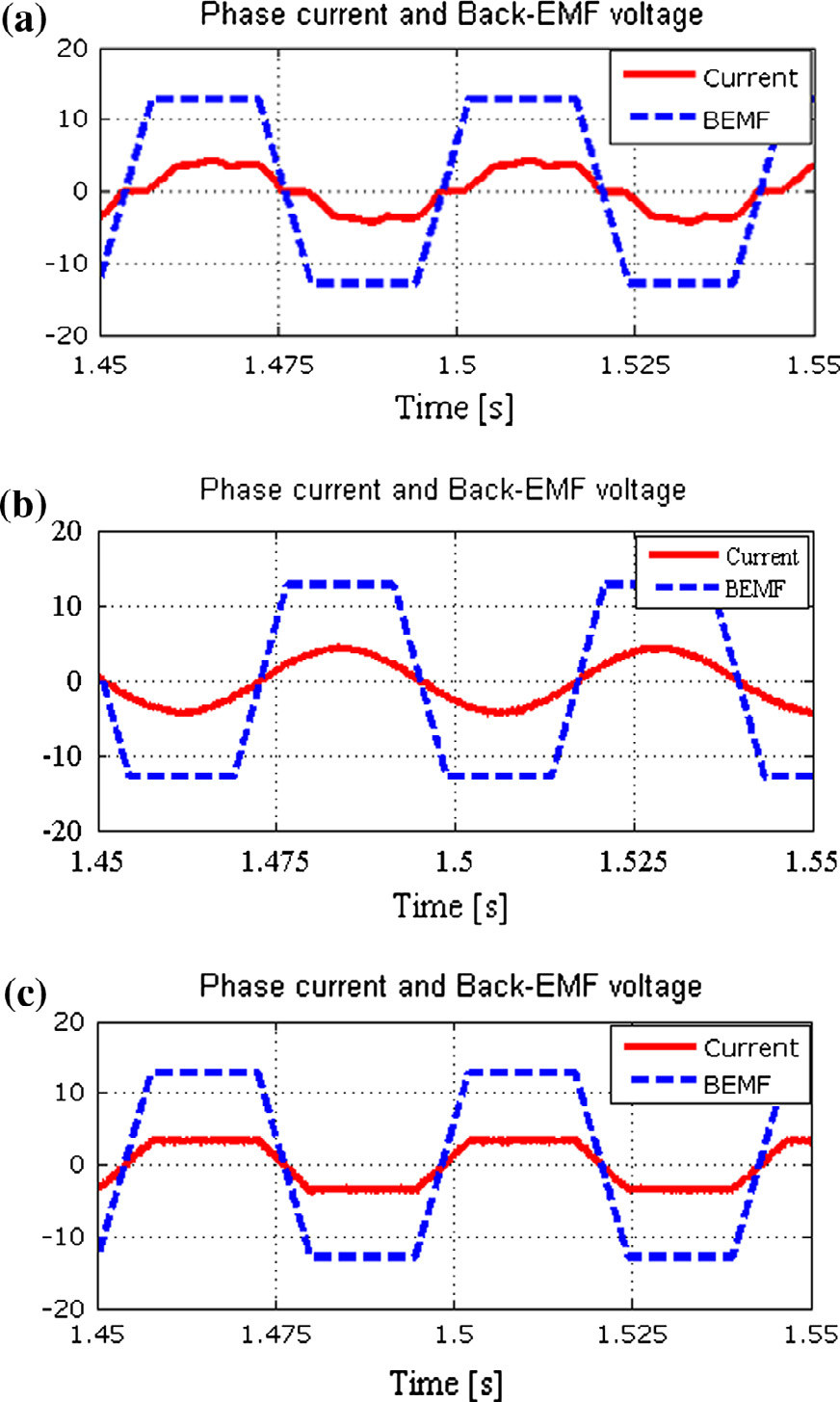
图5 显示了在450转/分钟转速下，无刷直流发电机在上述三种情况下的仿真结果，包括梯形相位反电动势电压和电流波形。在第一种情况下，当使用全桥二极管整流器作为无刷直流发电机的交流/直流变换器时，电流波形取决于转速和负载。由于电流未受控制，受相电感引起的相位延迟影响，会产生一定的畸变，因此该拓扑结构的效率较低。

在第二种情况下，采用滞环控制器产生正弦参考电流。该电流波形并不理想，因为电压和电流的所有谐波分量并未全部参与功率的产生。在第三种情况下，通过滞环控制器使无刷直流发电机产生梯形相电流。由于电压和电流具有相同的形状，所有谐波分量均参与功率的产生。

如图6 所示，在三种情况下，随着转速升高，电流畸变增大，这是由于电感引起的延迟增加所致。无刷直流发电机的数值结果总结于表1中。在450转/分钟速度下，采用梯形电流参考时，发电机功率相比全桥二极管整流器提高了6.8%；在1000转/分钟转速下，功率提高了11.6%。在更高速度下，由于电压与电流之间的相位偏离现象，功率增量将更大。在任何转速下，梯形电流的功率均高于正弦电流。

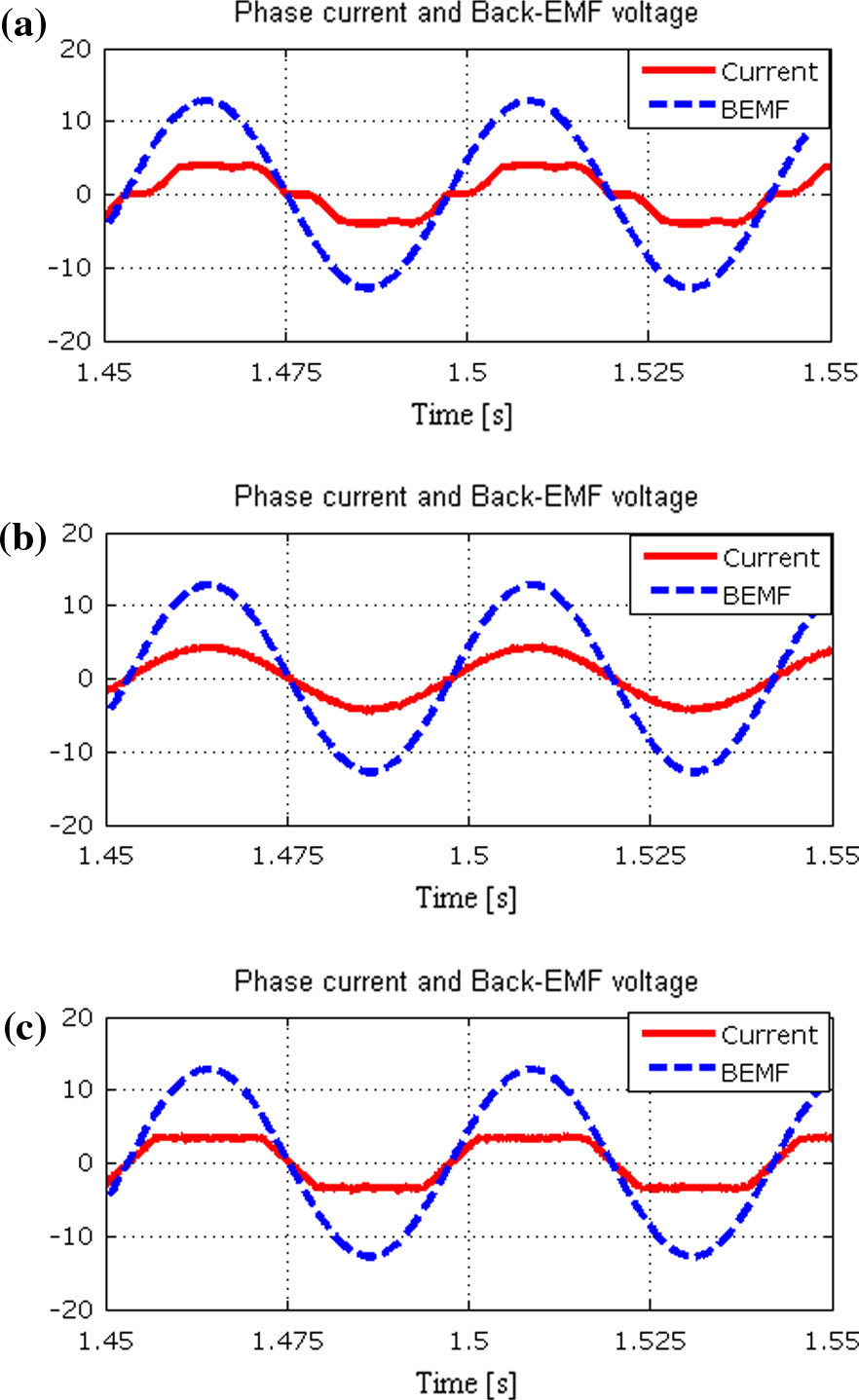
已对PMSG进行了相同的仿真和分析。图7显示了在450 转/分钟速度下，PMSG采用无源整流器和有源整流器时，正弦和梯形参考电流波形的仿真结果。由于感应反电动势电压为正弦波形，因此预计正弦波形为最优电流波形。

使用全桥二极管整流器，(b) 使用有源整流器配合正弦参考电流，以及(c) 梯形参考电流。)

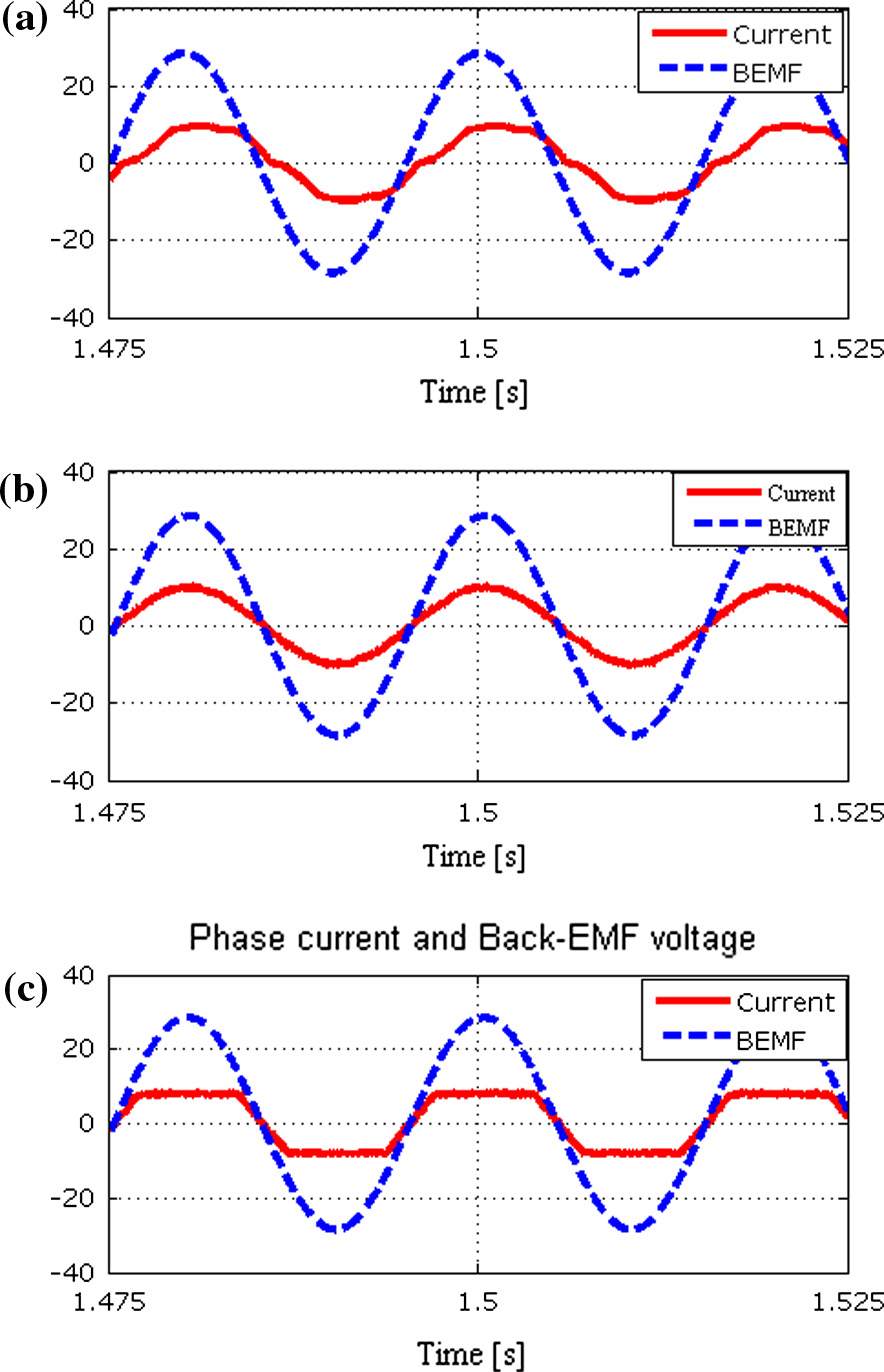
在1000转/分钟转速下PMSG的仿真结果如图8所示。使用无源整流器时存在较大的电流畸变，且在更高速度下畸变增大。PMSG的数值结果总结于表2中。在450转/分钟速度下，采用正弦电流时发电机功率比使用全桥二极管整流器提高了4.3%。在1000转/分钟转速下，该功率增量达到10.2%。对于梯形参考电流，在450转/分钟和1000转/分钟转速下的功率增量分别为1.8%和7.5%，均低于正弦情况。需要注意的是，有效值电流以及定子铜损保持恒定。

使用全桥二极管整流器，(b) 使用有源整流器配合正弦参考电流，以及(c) 梯形参考电流。)

表1 无刷直流发电机功率的比较

转速（转/分钟）	450	450	450	1000	1000	1000
	全桥二极管整流器	滞环控制 梯形	滞环控制 正弦	全桥二极管整流器	滞环控制 梯形	滞环控制 正弦
均方根电流（安培）	3	3	3	7	7	7
功率（瓦特）	95.2	101.7	99.2	472.8	527.7	514
增加（%）	–	6.8	4.2	–	11.6	8.7

表2 永磁同步发电机功率比较

转速（转/分钟）	450	450	450	1000	1000	1000
	全桥二极管整流器	滞环控制 梯形	滞环控制 正弦	全桥二极管整流器	滞环控制 梯形	滞环控制 正弦
均方根电流（安培）	3	3	3	7	7	7
功率（瓦特）	78.1	79.5	81.5	384.1	413	423.3
增加（%）	–	1.8	4.3	–	7.5	10.2
### 4. 实验结果
为了验证所开发的控制方法以及仿真和分析结果，设计并构建了一个实验平台。图9展示了整体实验系统装置。如图9（a）左侧所示，采用一台永磁直流电机作为系统的原动机，一台三相永磁同步电机作为发电机。由于实验室缺少合适的梯形波无刷直流发电机，因此实验结果仅针对永磁同步发电机给出。发电机的输入功率或轴转速可通过调节PMDC的电枢电压来改变。PMSG和PMDC电机的规格见附录A。如图9(b)所示，采用基于功率MOSFET的三相有源整流器，并使用电流和电压霍尔效应传感器进行电流调节和功率计算。电气负载采用可变电阻。所有控制和测量均通过低成本微控制器ATXMEGA128A3U实现。

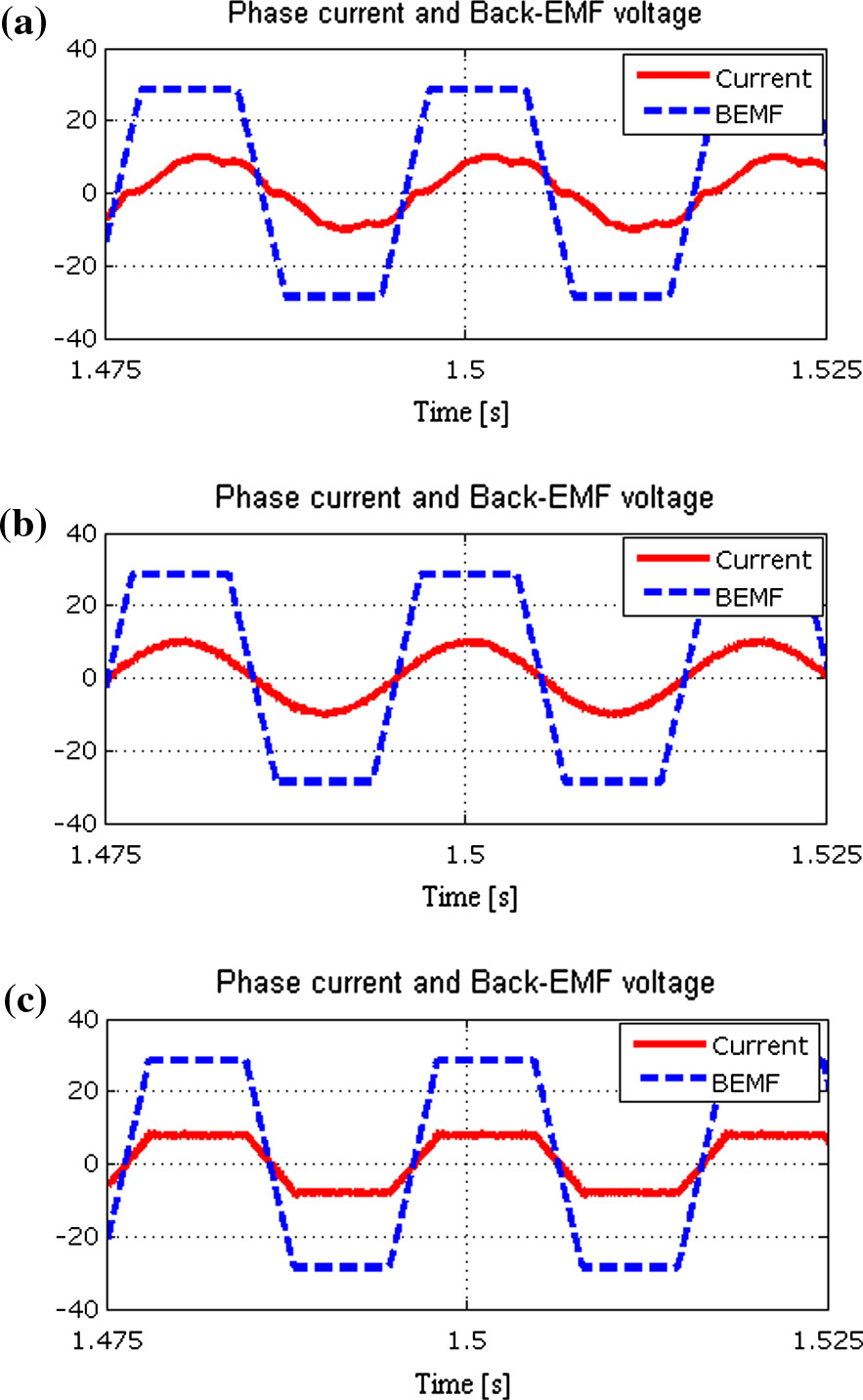
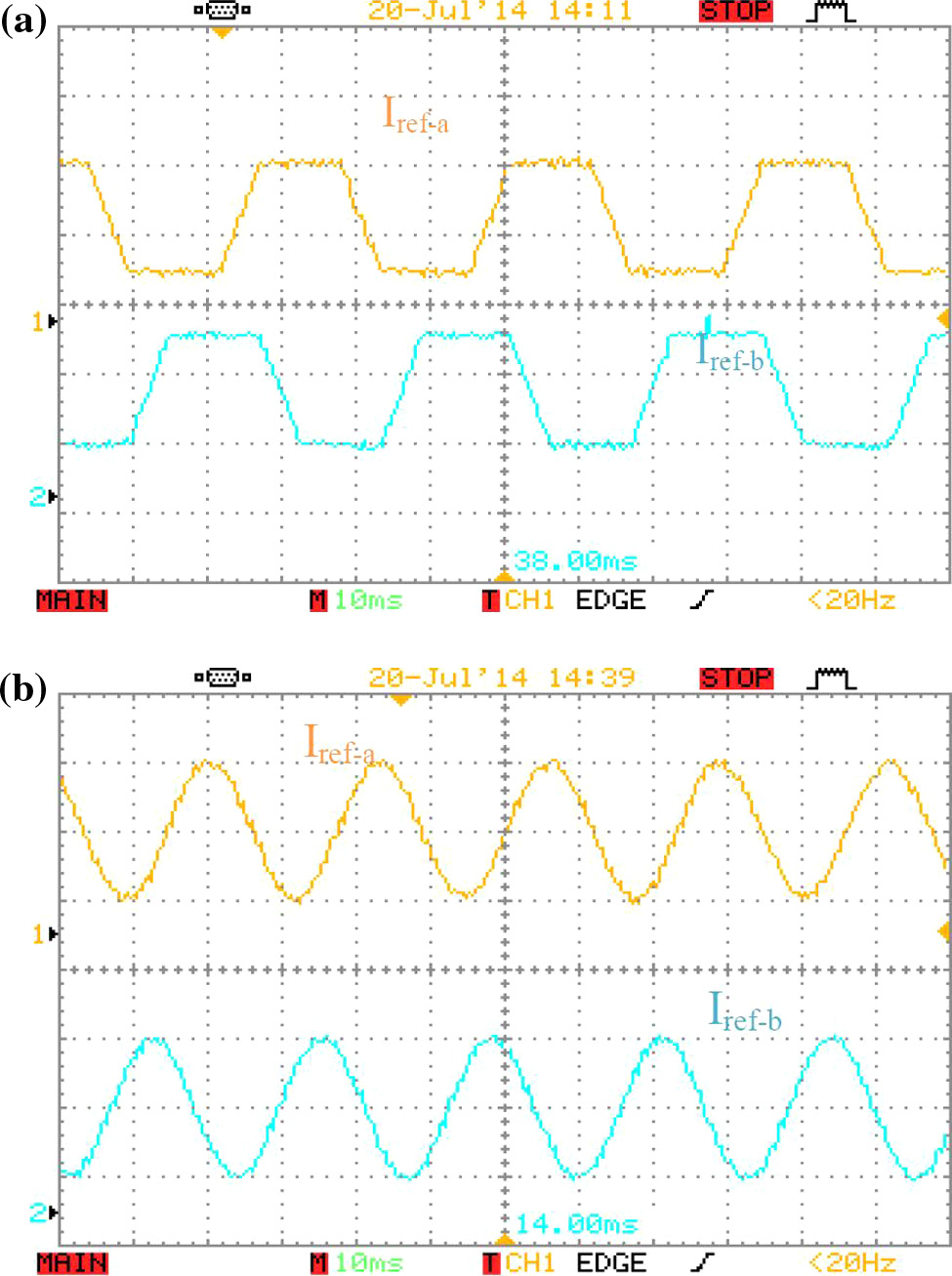
首先，将一个全桥二极管整流器连接到永磁同步发电机（PMSG）。图10显示了发电机在两种不同转速下的相电压和电流波形。此时对电流没有控制，因此永磁同步发电机的相电压和电流不同相，这在高速时更为明显。不同实验结果的一些计算总结于表3中。

450转/分钟转速下；(b) 1000转/分钟转速下。)

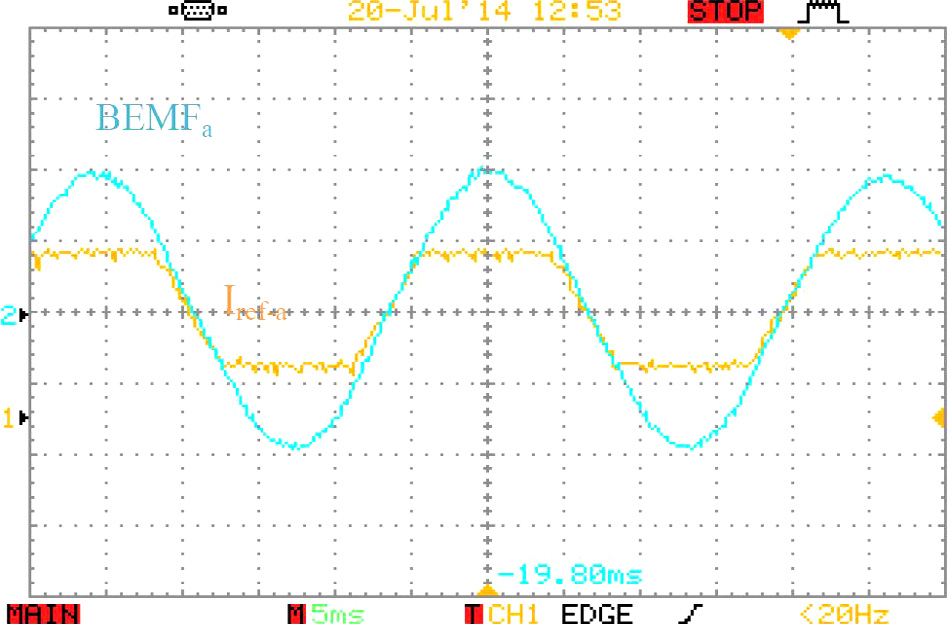
如图11所示，梯形和正弦形状的参考电流在微控制器中生成。为了生成梯形参考电流，可根据公式(4)使用霍尔效应位置传感器；而为了生成精确且同相的正弦参考电流，则应使用轴编码器。图12显示梯形参考电流与反电动势电压完全同相。

梯形电流和(b) 正弦电流。)

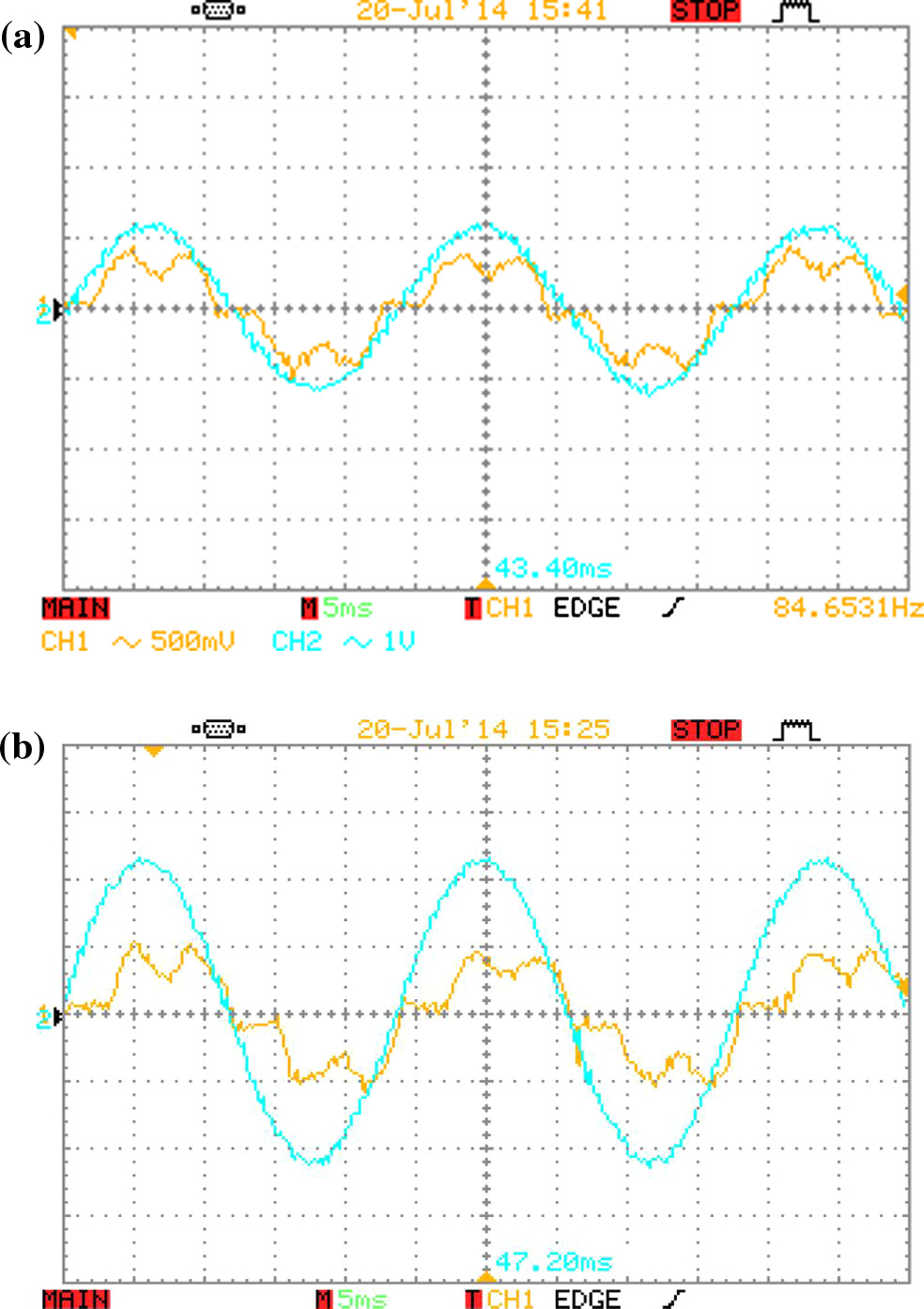
现在使用有源整流器。图13和图14分别显示了在450转/分钟和1000转/分钟两种转速下，梯形和正弦参考电流情况下发电机的电流波形。滞环电流调节器的性能令人满意，且相电流能够跟踪其对应的参考都很好。

450 转/分钟转速下；(b) 1000转/分钟转速下。)

上述三种情况的功率测量结果总结于表3中。在每种转速下，保持有效值电流（定子铜损）恒定。根据给出的结果，在450转/分钟速度下，正弦参考电流的功率比使用全桥二极管整流器时增加了4.1%；在1000转/分钟速度下，功率增加了10%。在所有转速下，正弦波形的功率增量均大于梯形情况。表2和表3的仿真与实验结果之间存在一些差异，这可能是由于仿真中所用数据不够精确所致。

表3 永磁同步发电机的实验结果。

转速（转/分钟）	450	450	450	1000	1000	1000
	全桥二极管整流器	滞环控制 梯形	滞环控制 正弦	全桥二极管整流器	滞环控制 梯形	滞环控制 正弦
均方根电流（安培）	3	3	3	7	7	7
功率（瓦特）	73	74.3	76	328	352.2	360.8
增加（%）	–	1.7	4.1	–	7.3	10

5. 结论

提出了一种用于最大化无刷直流电机和永磁同步发电机每安培功率和效率的控制技术。该方法基于相电流控制。针对两种发电机均进行了仿真，并利用功能强大的XMEGA微控制器对永磁同步发电机进行了实验。在两项工作中，每安培功率和效率均得到提升。对于无刷直流发电机，最优电流波形为梯形，为了生成梯形参考电流，采用霍尔效应位置传感器代替成本较高的轴编码器。仿真结果表明，输出功率提高了11.6%。因此，通过使用最优控制方法，发电机的重量和体积可减少11.6%。

结果还显示，当无刷直流发电机的相电流采用正弦波形时，输出功率提升了8.7%。永磁同步发电机的实验结果表明，输出功率提高了10%。该控制方案可用于电动汽车和混合动力电动汽车的再生制动，或用于优化发动机运行，使发动机工作在最优区域。