简谐震动简单分析

最新推荐文章于 2023-11-20 16:39:22 发布

papaofdoudou

最新推荐文章于 2023-11-20 16:39:22 发布

阅读量2.4k

点赞数 9

分类专栏：数学工程文章标签：目标检测深度学习人工智能

本文链接：https://blog.csdn.net/tugouxp/article/details/114552157

版权

数学同时被 2 个专栏收录

151 篇文章

订阅专栏

工程

53 篇文章

订阅专栏

之所以记录一下简谐震动，是因为最近在看拉普拉斯变换的时候，发现简谐震动和正弦有关系，正弦和傅里叶级数有关，傅里叶级数直接导出傅里叶变换，而傅里叶变换是拉普拉斯变换的一个特例，所以从简单的简谐运动开始分析，记录一下学习的足迹．

简谐运动，又称为简谐震动，谐震，SHM(simple Harmonic motion), 即是最简单也最基本的一种机械震动，当某物体进行简谐运动时，物体所受到的力跟位移成正比，并且力总是指向平衡位置．

如果用表示物体收到的回复力，用表示物体对于平衡位置的位移，根据胡克定律，正比于,她们之间的关系可以用下式来表示：

F=-kx

式中的是回复力与位移成正比的比例系数，负号的意思是，会复力的方向总跟物体位移的方向相反．

根据牛二定律

F=ma

一定质量的物体，加速度和物体所收到的和外力大小成正比，跟合力的方向相同，并且如果是孤立系统，系统的机械能守恒．

动力学方程：

对于简谐运动，其动力学方程是２阶微分方程，可以由牛顿第二运动定律得到：

$F=ma=m\frac{d^2x}{dt^2}=mx''$

F=-kx

所以：

mx''+kx=0

也就是：

$x''+\frac{k}{m}x=0$

这是一个二阶常系数齐次线性微分方程

可以先求出它的两个解 x_1,x_2 ,如果他们的比不为常数，也就是 x_1,x_2 线性无关，那么

x(t)=c_1x_1(t)+c_2x_2(t)

就是方程的一个通解．

当为常数时，指数函数 $y=e^{rx}$ 和它的各阶导数都只相差一个常数因子，由于指数函数这个特点，我们可以用 $x(t)=e^{rt}$ 来尝试，看能佛选取适当的，使得 $x(t)=e^{rt}$ 满足上面方程的解.

所以:

$r^2e^{rt}+\frac{k}{m}e^{rt}=0$

所以

$r^2+\frac{k}{m}=0=>r=\pm i\sqrt{\frac{k}{m}}$

所以，它的两个特根为：

$x_1(t)=e^{-i\sqrt{\frac{k}{m}}}=cos(\sqrt{\frac{k}{m}} \cdot t)-i sin(\sqrt{\frac{k}{m}} \cdot t)$

$x_2(t)=e^{i\sqrt{\frac{k}{m}}}=cos(\sqrt{\frac{k}{m}} \cdot t)+i sin(\sqrt{\frac{k}{m}} \cdot t)$

所以：

$X_1(t)=\frac{x_1(t)+x_2(t)}{2}=cos(\sqrt{\frac{k}{m}} \cdot t)$

$X_2(t)=\frac{x_1(t)-x_2(t)}{2i}=sin(\sqrt{\frac{k}{m}} \cdot t)$

所以，方程的通解是：

$\\ x(t)=c_1X_1(t)+c_2X_2(t)=c_1\cdot cos(\sqrt{\frac{k}{m}} \cdot t)+c_2\cdot sin(\sqrt{\frac{k}{m}} \cdot t)\\=Acos(\omega t-\varphi )$

转换形式：

$\\ Acos(\omega t-\varphi )=Asin(\frac{\pi}{2}-\omega t+\varphi )=Asin(\pi-\frac{\pi}{2}+\omega t-\varphi )=Asin(\omega t+\frac{\pi}{2}-\varphi )=Asin(\omega t + \phi )$

$\omega=\sqrt{\frac{k}{m}}$

$A=\sqrt{c_1^2+c_2^2}$

$tan(\varphi )=\frac{c_2}{c_1}$

$tan(\phi )=\frac{c_1}{c_2}$

$\phi +\varphi =\frac{\pi}{2}$

c_1,c_2 是由初始条件决定的常数，取平衡位置为原点，每一项都有物理意义，是振幅， $\omega$ 是角频率， $\varphi$ 是相位．

根据速度，加速度与位移量的关系，可以得到：

$v(t)=\frac{dx}{dt}=-A\omega sin(\omega t-\varphi )$

$a(t)=\frac{d^2x}{dt^2}=\frac{dv}{dt}=-A\omega^2 cos(\omega t-\varphi )$

$\omega=\sqrt{\frac{k}{m}}$

$\omega=\sqrt{\frac{k}{m}}=2\pi f=>f=\frac{1}{2\pi}\sqrt{\frac{k}{m}}$

$T=\frac{1}{f}=2\pi \sqrt{\frac{m}{k}}$

机械能守恒:

系统总机械能为动能+弹簧势能:

$\\ E=\frac{1}{2}mv^2(t)+\frac{1}{2}kx^2(t)=\frac{1}{2}mA^2\omega^2sin^2(\omega t - \varphi )+\frac{1}{2}kA^2cos^2(\omega t- \varphi) \\=\frac{1}{2}mA^2\frac{k}{m}sin^2(\omega t - \varphi )+\frac{1}{2}kA^2cos^2(\omega t-\varphi)\\=\frac{1}{2}kA^2sin^2(\omega t - \varphi )+\frac{1}{2}kA^2cos^2(\omega t- \varphi)\\=\frac{1}{2}kA^2[sin^2(\omega t-\varphi)+cos^2(\omega t- \varphi)]\\=\frac{1}{2}kA^2$

所以

$E=\frac{1}{2}kA^2$

能量守恒得证，根据这个结果，系统的总能量和弹性系数以及最大振幅有关，说白了，在 t_0 时刻，施加给系统的第一推动位置，决定了系统的总能量。

一图胜千言，看Geogebra如何描绘整个过程：

最外面蓝色圆圈表示位移变化，中间的绿色圆表示速度变化，最内层红色圆表示加速度的变化。

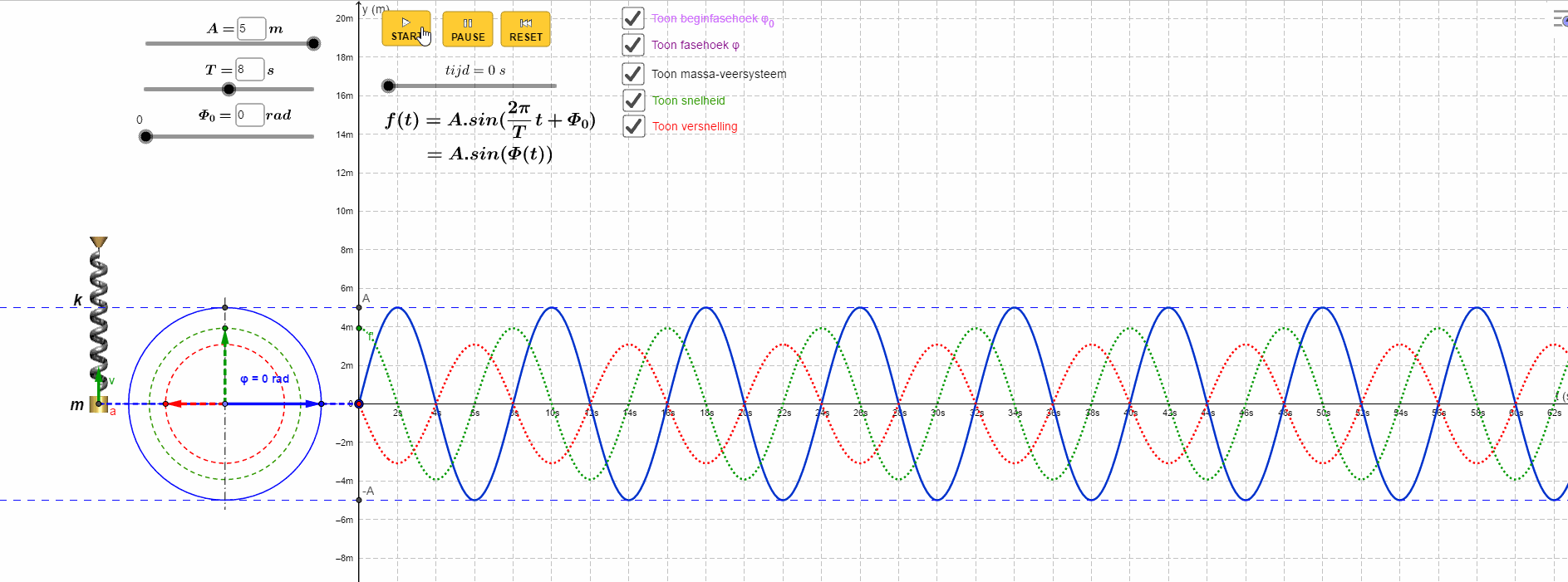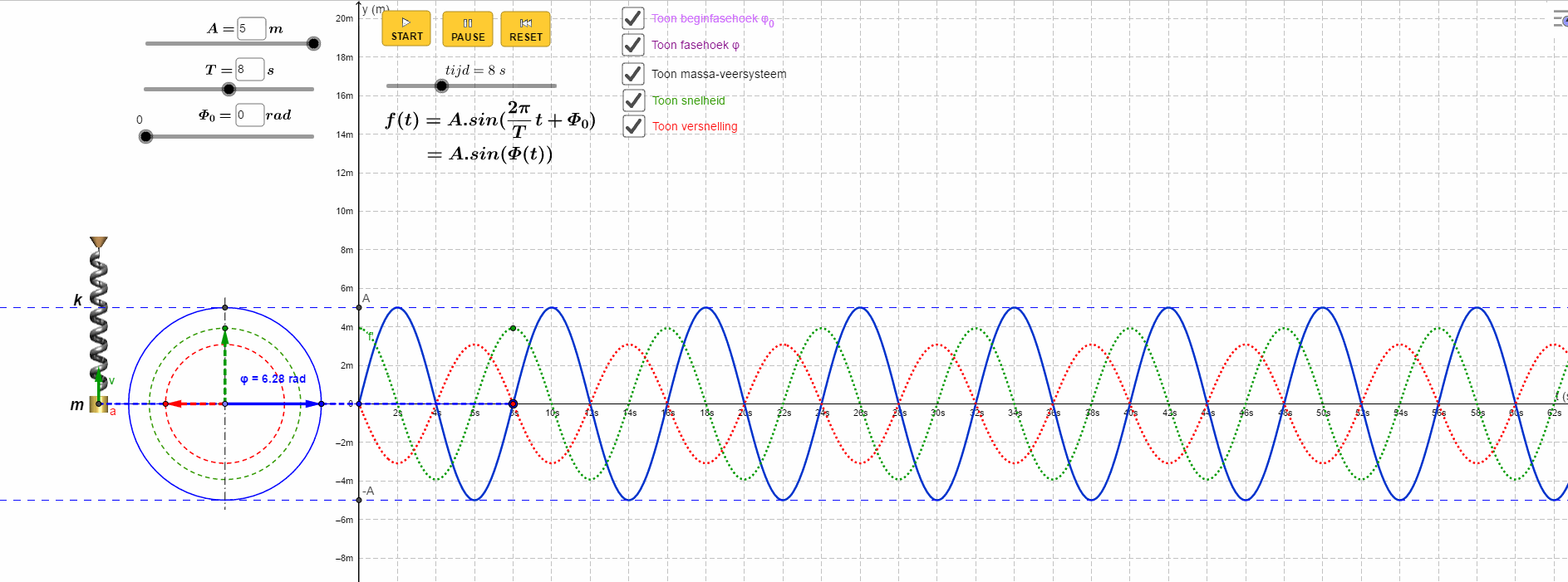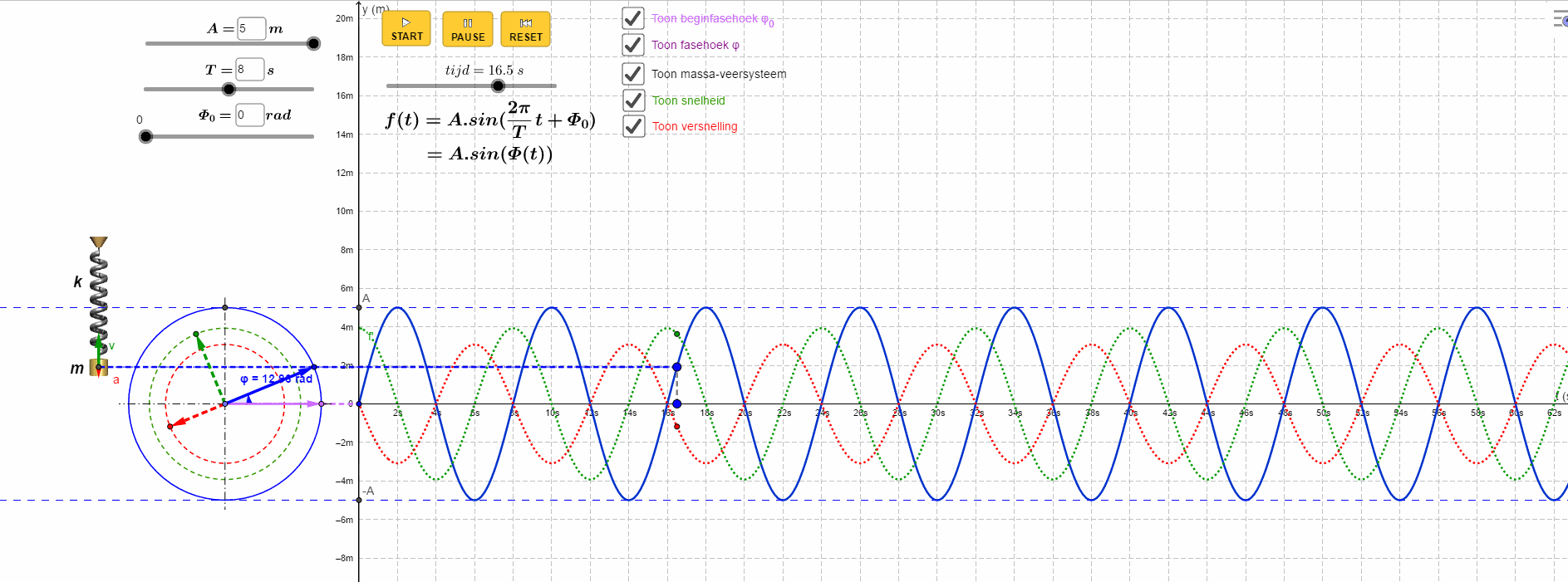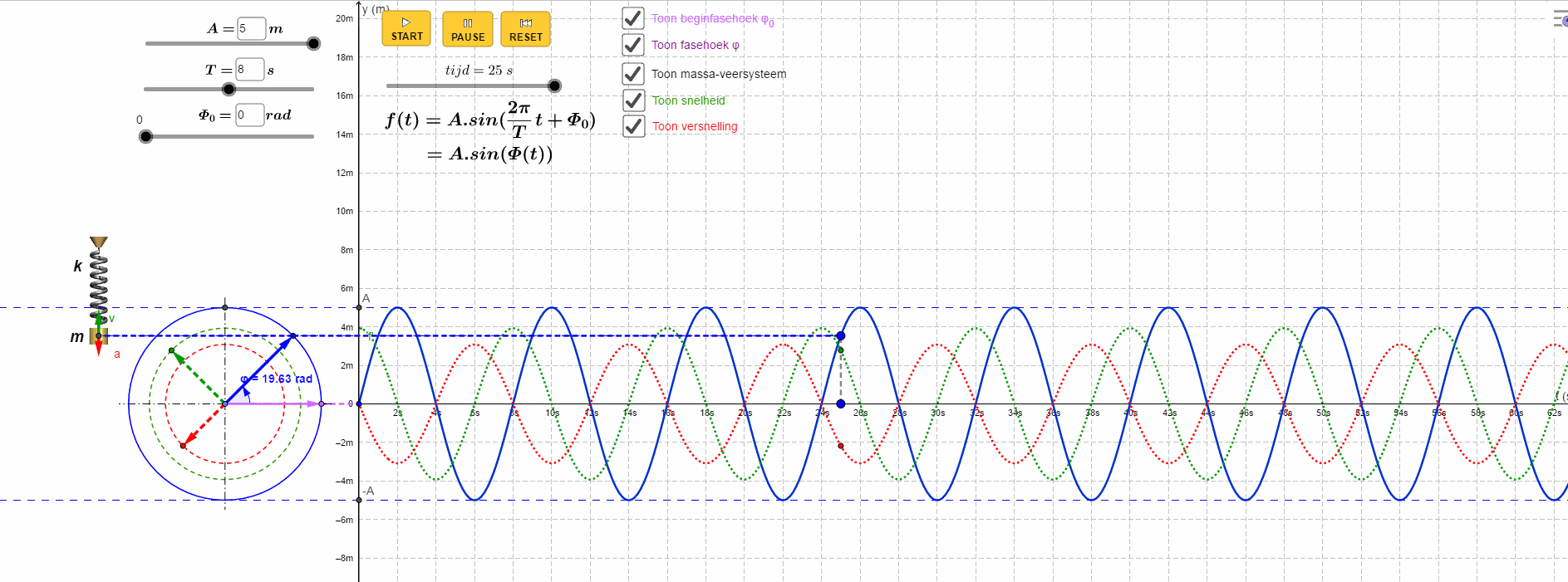
数学中有一类特殊的函数，它们有着非常良好的特性，比如三角函数，e指数函数，幂函数等等，你可以对它们不停求导而不会遇到奇点，也可以对它们进行泰勒展开，得到的收敛半径无穷大。更为特殊的是，某种意义上，它们似乎是构成其它函数的“元”函数，大部分的函数都可以用以上几类函数做近似表示，它将我们从时域带入频域，进入另一个和我们的世界对偶的新世界。为什么三角函数这么特殊？这是科学家讨论的话题，我等小民无从知晓，不过，冥冥中有种感觉，这种基础的问题可能会将我们导向研究世界的本质，现代物理认为世界上的大部分现象都与波有关，包括宏观物体物质波，或许这种关系里面隐藏着更为深刻的真相，现代宇宙学中的“弦理论”，认为世界十一维的，所有的物质都是由极其微小的单元”弦“构成，弦的震动构成了多姿多彩的世界，又是震动，又是圆，这中间，是否蕴藏着某种更本质的东西等待我们去发现。