到底什么是“数学思维”？超越宇宙尺度的人类思维之美！

turingbooks

于 2024-02-08 11:30:27 发布

阅读量163

点赞数

文章标签：算法

原文链接：https://mp.weixin.qq.com/s?__biz=MjM5Njc0MjIwMA==&mid=2649810564&idx=1&sn=295da5331e17727651aa6a6665e5015c&chksm=bf9a97d92fdbaa5926beb34ec798982eded966a840f63cf4ae2bc10b4cafbe9bf686cfd8460b&scene=126&sessionid=0

版权

本文介绍了数学思维的重要性，通过吴军老师的观点和《思考的乐趣》一书中关于数学证明的内容，特别是范德瓦尔登定理，展示了如何通过染色问题理解数学的逻辑。文章还提及了几本关于数学的书籍，鼓励读者探索数学之美和思维的深度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

新年新气象，知识不打烊！

全场电子书惊喜6折，开启智慧成长年！

翻开新篇章，让心灵与知识一同远航。

错过等一年，现在就是囤书的最好时光！

（PS：新上电子书不参与本次活动哦，小编多帮大家争取了半天时间，8号中午12点优惠就开始了，不要被老板发现）

吴军老师说，数学思维，不仅能让你登上更高的高度，开拓你的眼界，也能够帮你建立一些正确的常识，让你少走弯路，并且让你在人生的每一个岔路口，有更多更多的选择。

那么到底什么是数学思维呢？

数学科普大神顾森的这本《思考的乐趣》就从“生活中的数学”、“数学之美”、“几何的大厦”、“精妙的证明”和“思维的尺度”五个维度，用了大量的案例来展现数学的乐趣，每一个读过的人都会被深深吸引。

《思考的乐趣》出版至今，收到了十余万的读者的喜爱。今天就选取其中“史诗般壮观的数学证明”一节，为大家分享数学思维的尺度。

你认为，是否有可能把全体正整数染成红蓝二色，使得不存在无穷长的等差数列，满足数列中的所有数都是一种颜色？

事实上，满足题意的染色方案是存在的。例如，我们可以从数字1开始，把正整数染成一段红一段蓝，使得每一段的长度都是其前一段的两倍。也就是说，我们把1染成红色，2和3染成蓝色，4到7染成红色，8到15染成蓝色，依此类推，单色区间的长度成倍地增加。可以证明，如此染色后，一定不存在无穷长的单色等差数列。这是因为，假设某个等差数列的公差为，那么当单色区间的长度大于公差时，等差数列将会一截一截地落在不同的染色区间中，从而拥有不同的颜色。

有趣的是，把上述命题中的“无穷长”换成“任意长”，命题就不见得仍然正确了。1927年，荷兰数学家范•德•瓦尔登（Van der Waerden）证明了这么一个事实：对于任意大的正整数，总存在正整数，使得对从1到的正整数进行红蓝二染色后，不管你是怎么染色的，里面总存在一个单色的长度为的等差数列。当命题从两种颜色扩展到任意多种颜色时，该命题竟然也都成立。这个定理就叫做范德瓦尔登定理。下面，让我们来看看范德瓦尔登定理的证明过程。到了整个证明的最后一步，你一定会被震撼得说不出话来。

我们首先来证明的情况：存在某个使得对个连续自然数进行二染色后,里面总存在长为3的单色等差数列。我们把全体正整数5个5个地分组，1到5为第一组，6到10为第二组，以此类推。每一组里总共有种不同的染色方案，因此在前组里面必然有两个组的染色一模一样，比方说第7组和第23组吧。把第7组里的数分别记作，由鸽笼原理，、、里面一定存在两个颜色相同的数，不妨假设和都是红色吧。考虑的颜色：如果它是红色，我们的问题就解决了，已经是一个长度为3的等差数列。

下面考虑是蓝色的情况。别忘了第7组和第23组的染色完全相同，因此如果把第23组里的数分别记作，那么和也是红色，也是蓝色。下面我们来考虑全体正整数的第39组（注意到是等差数列），我们把它里面的5个数分别记作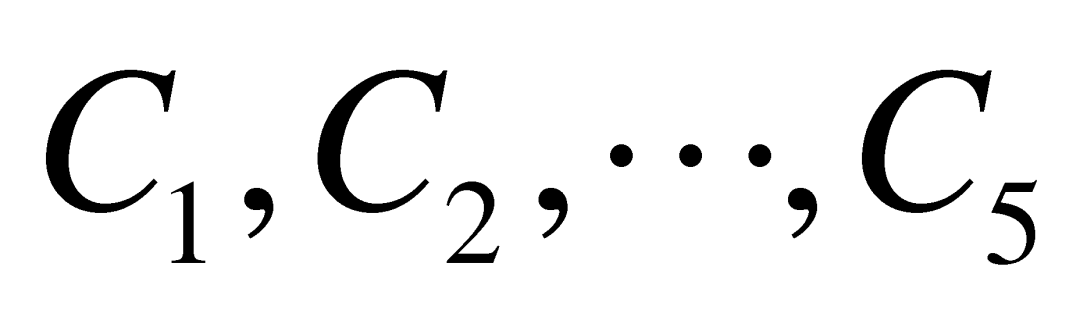。考虑的颜色：如果它是红色，那就是一个全为红色的等差数列，否则就是一个全为蓝色的等差数列。显然，上述证明中的“最坏情况”就是，第1组和第33组的染色相同，且第1组的第1个数和第33组的第3个数是红色的，则下一个数最远可以是第65组的第5个数，即全体正整数的第325个数。换句话说，时即满足条件。（这不一定是最小的，但确实是一个满足要求的。）

有意思的是，对任意的颜色数，上述证明都是适用的。比方说，当时，取，把全体正整数个个分为大组，在头组中必然存在两个染色一样的组，不妨把它们记作大组A和大组B。把这两个大组里的数分别都7个7个地分成个小组，在头组中，必然有两个小组的染色方案一模一样，比如小组a和小组b。

在每一个小组的前4个数中，必然有2个数的颜色是相同的，假设第1个数和第4个数是红色。那这个小组里面的第7个数要么是红色（问题已解决），要么是另一种颜色（比如蓝色）。将与前两个小组构成等差序列的第三个小组记作小组c，由于一个大组中有个小组，因此小组c一定还在该大组中。小组c中的第7个数要么是红色（问题已解决），要么是蓝色（问题已解决），要么是剩下的那种颜色（比如黄色）。那么，与两个大组构成等差序列的第三个大组（记作大组C）中，对于相应的小组c位置上的第7个数（图1中标记星号的位置）的颜色就没有任何选择了，它或者和每个大组的那个染黄色的数成等差数列，或者和大组A中的小组a的蓝色数、大组B中的小组b的蓝色数构成等差数列，或者是跨越层数最多的，和大组A中的小组a的第1个红色数、大组B中的小组b的第2个红色数构成等差数列。

图　1

类似地，对于更大的颜色数，我们都可以归纳证明，只不过分组的层数更多，底数也相应变大。因此，我们解决了且任意大时的情形。

真正令人震撼的时刻到了。接下来，我们将对施加归纳。下面尝试证明、的情况，即存在一个充分大的，使得对1到的正整数进行二染色后，里面总存在长度为4的单色等差数列。由于当时每325个数里面必然有一个等差数列，因此我们按每487个数一组进行分组。这样可以保证每一组里面的前325个数中总存在长为3的单色等差数列，并且该数列的第4个数也在该组内。注意，一个487元组共有种染色方案，如果我们把它们看做种不同的“广义颜色”，由、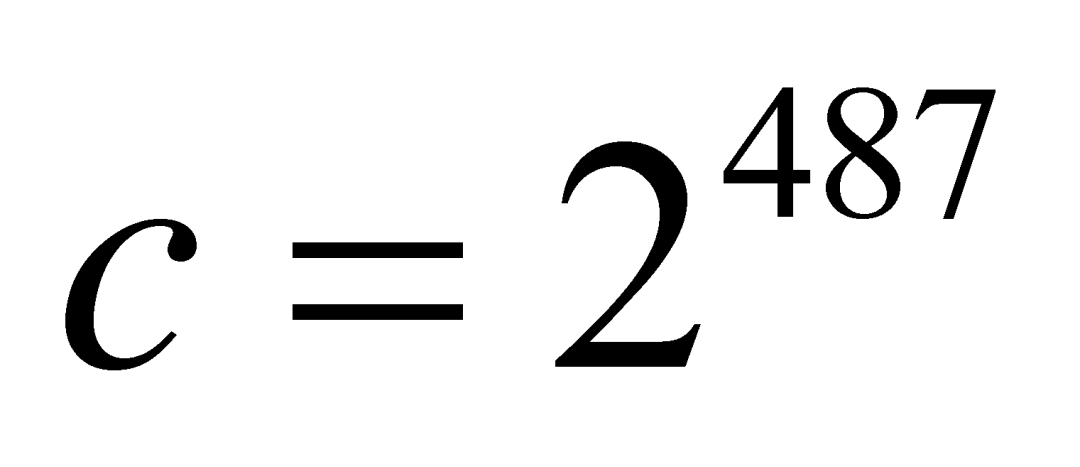的情况知，必然存在3个组，这3个组的位置形成等差数列，并且它们的染色方案完全相同。考虑每一组中前325个数所形成的长为3的等差数列，并考虑该数列中第4个数的颜色：如果颜色相同，问题解决；否则便考察顺推下去的第4个组的相应位置上的数的颜色，它将别无选择。

类似地，我们可以归纳出任意大的和任意大的的情形。可想而知，也可以说难以想象，用这种做法得出的是何等地巨大，它将很快超出整个宇宙中任何具有实际意义的数字，其大小已经不能用通常的方式来记录了。这个证明的气势太宏大了，以至于当初很多人都没想到。当我第一次读到种颜色时，视野一瞬间广大得难以描述；并且当我向着更大的方向看去时，不禁对思维的尺度表示深深的膜拜。

推荐阅读

《思考的乐趣：Matrix67数学笔记》

作者：顾森

中科院院士张景中、汤涛联袂推荐

本书是一个疯狂数学爱好者的数学笔记，面向所有喜爱数学的读者。本书包括5部分内容，即生活中的数学、数学之美、几何的大厦、精妙的证明、思维的尺度，涉及48篇精彩的文章。即使你不喜欢数学，也会为本书的精彩所倾倒。

这是一本标新立异的趣味数学书。每一个读过的人都会被深深吸引。这是一个热爱思考的年轻人积攒的让人一读就欲罢不能的趣味书。

新年新气象，知识不打烊！

全场电子书惊喜6折，开启智慧成长年！

翻开新篇章，让心灵与知识一同远航。

错过等一年，现在就是囤书的最好时光！

（PS：新上电子书不参与本次活动哦，小编多帮大家争取了半天时间，8号中午12点优惠就开始了，不要被老板发现）

《数学的雨伞下：理解世界的乐趣》

作者：[法] 米卡埃尔•洛奈（Mickaël Launay）

译者：欧瑜

惊讶！是思考的起点；

数学，是理解世界本质与万物关联的工具！

以数学为起点，以思考为快乐！

法国数学学会“达朗贝尔奖”得主科普名作。

数学，是理解世界本质与万物关联的工具，它能制造两个指南针：一个叫“实用”，一个叫“优雅”。不懂得数学的意义，就无法真正学习和理解数学。

科学家为什么那么聪明？因为他们有非凡的思考方法。

以数学为工具，以思考为快乐；培养自己的思考力、观察力，成为真正的思考者。

《数学女孩》（1-6）

作者：结城浩

译者：朱一飞等

日本数学会强力推荐，内容由浅入深，绝赞的数学科普书，在动人的故事中走近数学，在青春的浪漫中理解数学。

《数学女孩》系列以小说的形式展开，从基础数学到费马大定理、哥德尔不完备定理、随机算法、伽罗瓦理论、庞加莱猜想，重点描述一群年轻人探寻数学之美的过程。

《数学女孩的秘密笔记》系列（全7册）

作者：［日］结城浩

译者：陈朕疆/卫宫纮

全网已上市！持续热销中!

日本数学会强力推荐，热销超50万册。《数学女孩》全新延展系列。

初等数学科普×青春小说，数学再也不枯燥，在动人的故事中走近数学，在青春的浪漫中理解数学。

“数学女孩”系列以小说的形式展开，重点讲述一群年轻人探寻数学之美的故事，内容深入浅出，讲解十分精妙，被称为“绝赞的数学科普书”。“数学女孩的秘密笔记”是“数学女孩”的延伸系列。作者结城浩收集了互联网上读者针对“数学女孩”系列提出的问题，整理成篇，以人物对话和练习题的形式，生动巧妙地解说各种数学概念。