高中不讲，大学要用！多项式也能做除法？

在刚刚结束的高数衔接公开课上，宋浩老师为大家详细地讲解了多项式及其除法、和高次方程的内容。几千名同学齐聚线上课堂，进行了近3个小时的课程学习，结束时大家仍意犹未尽。在这篇文章中，我们来复习一下多项式的部分。

一、多项式概念

多项式是我们在中学时代就接触过的概念，只不过因为没有掌握更高级的数学语言，所以更多是通过具体例子来理解（见下图）。

但数学是一门语言统一、逻辑严谨、可以推理演绎的学科，在高等数学中，我们将用更为严谨的数学语言给出定义，因此多项式的严格定义为：

注意，这里的x是一个符号，可以表示变量（如数字），也可以表示矩阵（线性代数中的一个重要概念）等其他含义，因此这个定义中的多项式是一种形式上的表达式，是对我们中学所学多项式的推广。

多项式在线性代数和概率论的应用

此外，多项式与方程、函数、不等式等有着密切的联系。例如我们在中小学阶段接触的乘法公式，其展开式就是多项式。

我们可以根据上图中的一系列公式推广出的多项式展开（具体的数学证明不在此展示），即：

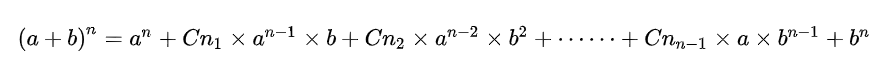
别看上面这个式子很长，但是记忆也是有规律可循的，其中的高次幂、两个常数的幂次都是有递增或递减规律的，大家可以试着自己发现一下。这里展示常用的乘法公式，方便大家收藏记忆。

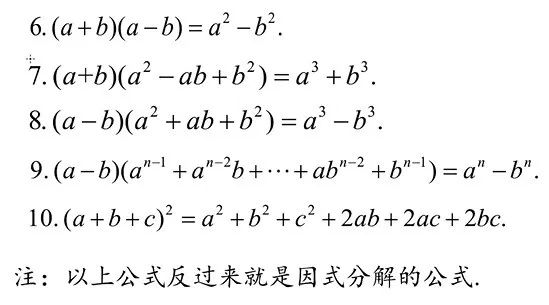
因式分解与解高次方程有密切的关系。

二、多项式的除法

多项式的除法是高等数学和线性代数经常会用到的计算类型，无论是解方程、解不等式，还是在线性代数中求特征值，我们都会用到多项式的除法。简单理解就是，多项式除法就像整数除法一样是除法的一种类型，只不过除项和被除项是多项式，俗称「长除」。它的严格数学定义为：

多项式的除法有一系列特别深奥的结论，非数学的同学就不用去看这些结论了，我们就直接通过例题来给大家讲多项式怎么样做除法？解多项式除法采用竖式除法：

(1)把被除式和除式降幂排列，缺项用0补齐;

(2)用被除式的第一项去除除式的第一项，得商式的第一项；

(3)用商式的第一项去乘除式，把积写在被除式的下面(同类项对齐)做减法;

(4)把差当作新的被除式，重复上面的做法，直到余式为0或次数低于除式的次数为止。

至此，关于多项式除法的思想和应用就清晰了，更多的定理和定义无非是对定理一的推广和变形，具体定理放到下方：

限于篇幅在此就不赘述了。

这里多说一句，题目中往往用函数f(x)或者g(x)表示一个多项式，大家不要因为符号多而畏难，很多时候我们为了求解去试数不会超过±5（毕竟老师也知道大家考试的时间有限）。多熟悉数学符号、熟悉公式的叫法会对大家的解题大有裨益。

三、一个著名的多项式

在包括数论、分析数论、调和分析、量子计算等领域，有一个核心概念不断被提及、研究和广泛应用，这就是狄利克雷多项式。它是一类特殊的函数，其一般形式可以表示为：

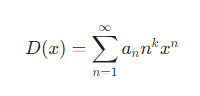
其中:

·是多项式的值,

· 是系数，

· 是自然数，

· 是一个非负整数，

· 是变量。

这里用了∑符号来简化了多项式的加法，感兴趣的同学也可以把这个式子展开看看。狄利克雷多项式以德国数学家彼得·哥特弗里德·狄利克雷的名字命名，他是高斯的学生，也是解析数论的创始人。他的成果为世人所知的有：抽屉原理、函数的现代定义……对数学分析、复分析、数论和代数都有着重要贡献。

狄利克雷多项式之所以著名，主要是因为它在数学和物理学中扮演了关键角色，特别是在数论和分析数论中：

代数函数的生成函数：

狄利克雷多项式是某些代数函数的生成函数，这些函数在数论中非常重要。通过狄利克雷多项式，可以研究代数函数的性质，如它们的增长速度和周期性。

素数分布和解析数论：

狄利克雷多项式与素数分布和解析数论有密切关系。例如，素数的倒数和可以通过狄利克雷多项式来表示，这有助于理解素数的分布规律。

调和分析：

狄利克雷多项式在调和分析中与傅里叶级数和傅里叶变换有联系，它们帮助研究周期函数的性质。

量子计算：

在量子计算中，狄利克雷多项式的性质可能被用于设计新的量子算法。例如，它们与量子态的叠加和纠缠有关。

在刚开始的非数学专业的高数学习中，很多人可能暂时应用不到这些内容，大家可以根据自己的专业有选择地进行了解。

以上知识点视频课程已加入「高数共学营」下划了解详情↓↓

同时，衔接课课后练习题宋老师也给大家准备好了，联系群主小希领取~

参考资料：

《宋浩高数共学营（上学期）》高数衔接课  宋浩老师&图灵社区 联合出品

  第三部分内容来源于网络素材整理，如百度百科等

这是一系列直播大课和社群服务，

在这里你将获得：

01

10+场直播全程陪伴

本期共学营将会有不少于10场的宋浩老师直播大课，紧贴大学课程进度进行重难点精讲，讲解知识要点技巧、解题思路和步骤，逐步掌握解题过程，提高解题效率和准确率；在期中和期末考试前进行知识串讲，帮助大家回顾和巩固整个学期的学习内容。

02

阶段测试与模拟试卷

根据学习进度定制高数上学期期中期末模拟测试卷并对试题进行详细讲解，让学生能够及时检验学习成果，查漏补缺，加深对知识点的理解；找出进度差距，督促学习。

03

知识点覆盖范围全面

一般学校只讲到不定积分，有的学校可能学到定积分的应用，少部分学校可能讲完微分方程，宋浩老师将在本期高数共学营中带大家完成高等数学上册全部知识点，同学们可以根据自己的需求有侧重地进行学习。

04

科学安排学习进度

细分每周学习内容，将高数上册内容分解成3个月的进度表，根据教材重点安排必做习题（教材课后习题和精选750题）。进度！进度！进度！帮助同学们按进度完成学习任务。

早鸟优惠倒计时！

99元/学期

随营赠礼：宋浩老师已经录制的100题讲解[一题一解]

加入共学营可观看往期回放

领取宋老师上课手写讲义