
在数学发展的过程中,很多时候提出新的数学问题,开创新的数学领域,最初的动机并不是解释生活中的现象,而是因为它本身的美妙。几乎所有的数学家都认为数学是优美的。而普通人要如何感受数学的美呢?
数学科普大神顾森的这本《思考的乐趣》就从“生活中的数学”、“数学之美”、“几何的大厦”、“精妙的证明”和“思维的尺度”五个维度,用了大量的案例来展现数学的乐趣,每一个读过的人都会被深深吸引。这是一个热爱思考的年轻人积攒的让人一读就欲罢不能的趣味书。《思考的乐趣》出版至今,收到了十余万的读者的喜爱。
今天就选取书中那些关于有趣“神秘的数学常数”与大家一起分享数学的美。
我一直觉得,数学中的各种常数是最令人敬畏的东西,它们似乎是宇宙诞生之初上帝就已经精心选择好了的。那一串无限不循环的数字往往会让人陷入一种无底洞般的沉思——为什么这串数字不是别的,偏偏就是这个样呢?除了那些众所周知的基本常数之外,还有很多非主流的数学常数,它们的存在性和无理性同样给它们赋予了浓重的神秘色彩。现在,就让我们一起来看一看,数学当中到底有哪些神秘的常数。
01
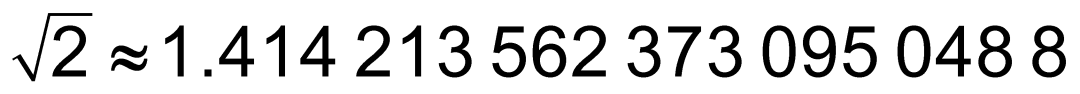
古希腊的大哲学家毕达哥拉斯(Pythagoras)很早就注意到了数学与大千世界的联系,对数学科学的发展有着功不可没的贡献。他还创立了在古希腊影响最深远的学派之一——毕达哥拉斯学派。毕达哥拉斯学派对数字的认识达到了审美的高度。他们相信,在这个世界中“万物皆数”,所有事物都可以用整数或者整数之比来描述。
然而,毕达哥拉斯学派的一位叫做希帕索斯(Hippasus)的学者却发现,边长为1的正方形,对角线的长度不能用整数之比来表示。这一发现无疑触犯了学派的信条,因此希帕索斯的命运非常悲惨,最后被溺死在了大海之中。与此有关的历史记载非常模糊,因此后人开始添油加醋,演绎出了这段故事的诸多版本,希帕索斯为何而死也是众说纷纭。不管怎样,希帕索斯都被人们当作了发现无理数的第一人。
利用勾股定理可知,边长为1的正方形,对角线的长度就是方程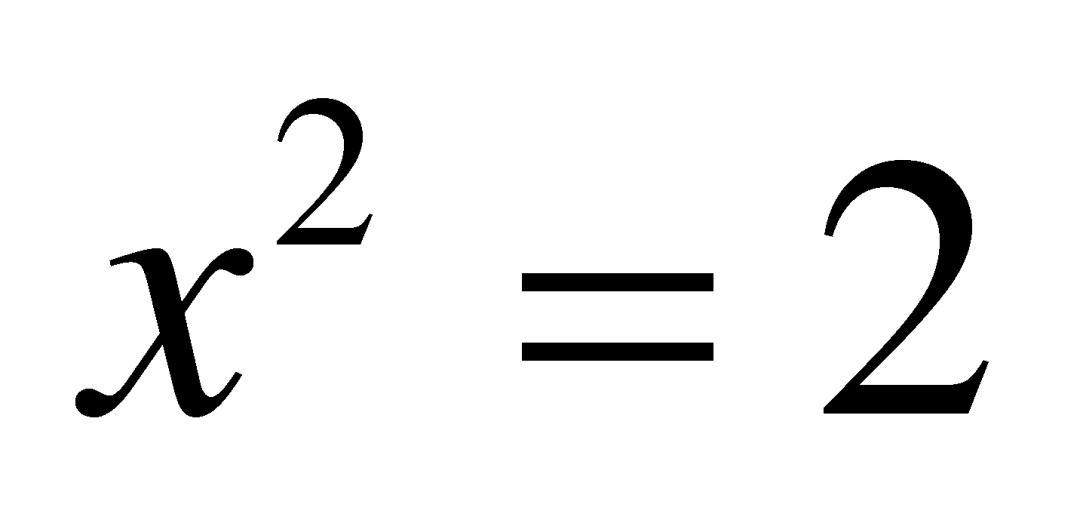 的唯一正数解,我们通常把它记作
的唯一正数解,我们通常把它记作![]() 。
。![]() 可能是最具代表性的无理数了,证明它的无理性有很多种方法。最常见的一种就是下面这个反证法:假设
可能是最具代表性的无理数了,证明它的无理性有很多种方法。最常见的一种就是下面这个反证法:假设![]() 可以表示成
可以表示成![]() ,并且假设
,并且假设![]() 已经是一个最简分数了。那么
已经是一个最简分数了。那么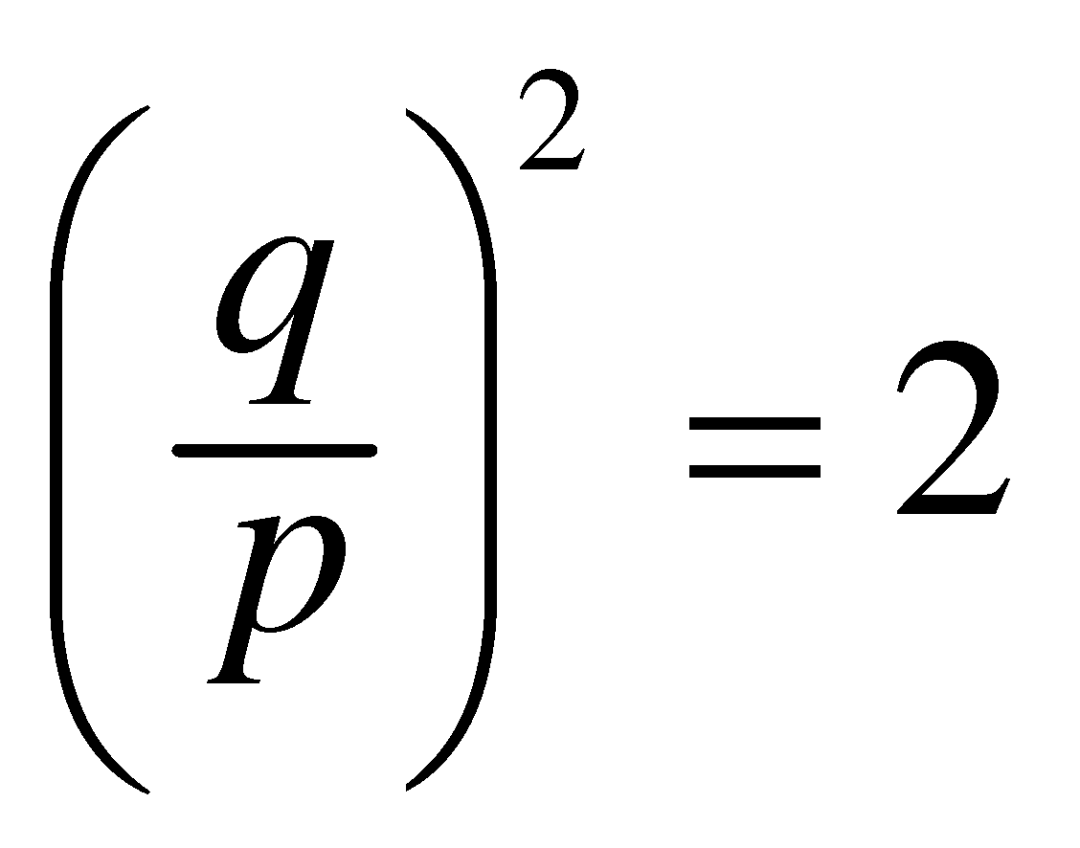 ,也即
,也即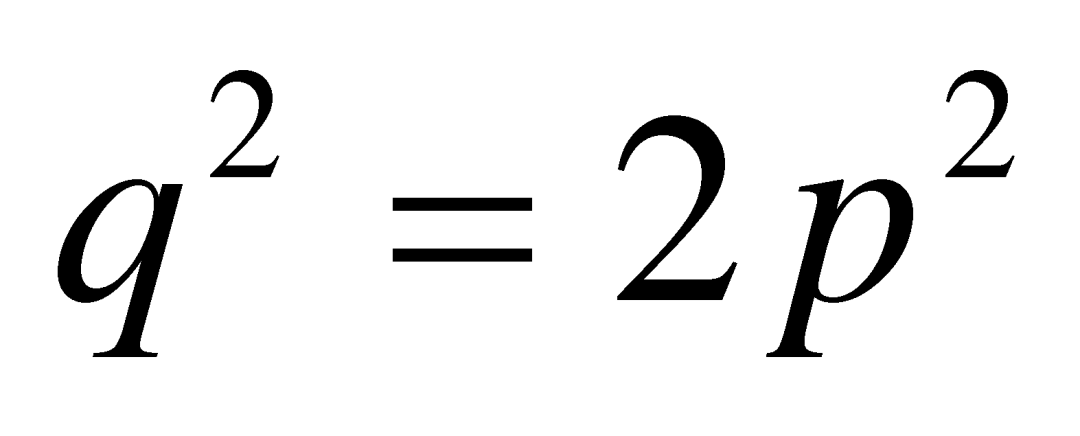 。这说明
。这说明![]() 是个偶数。但只有偶数的平方才能等于偶数,因此
是个偶数。但只有偶数的平方才能等于偶数,因此![]() 一定是偶数。
一定是偶数。![]() 是偶数就说明
是偶数就说明![]() 能被4整除,等式两边约掉一个2,可见
能被4整除,等式两边约掉一个2,可见![]() 也是偶数,从而
也是偶数,从而![]() 是偶数。这样,
是偶数。这样,![]() 也是偶数,
也是偶数,![]() 也是偶数,那么
也是偶数,那么![]() 和
和![]() 就还可以继续约分,与我们的假设矛盾。
就还可以继续约分,与我们的假设矛盾。
证明还可以更简单一些。同样假设![]() 已经是最简分数了,那么
已经是最简分数了,那么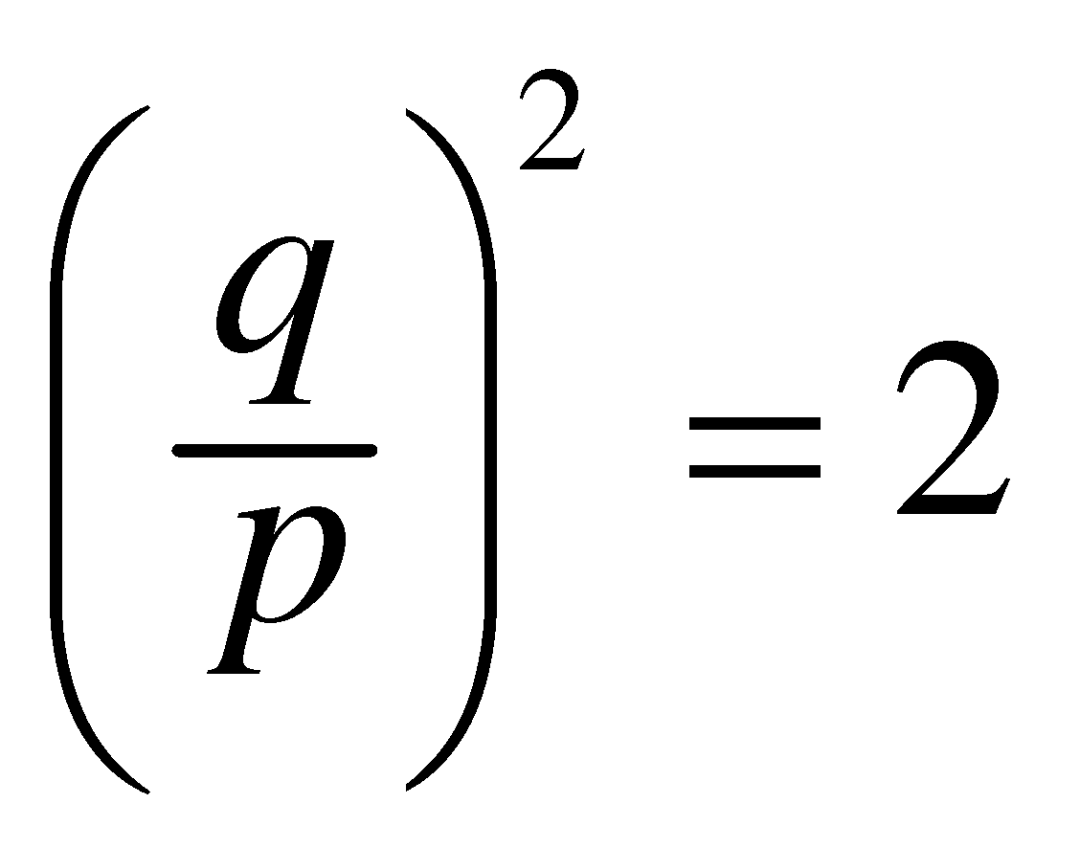 ,也就是
,也就是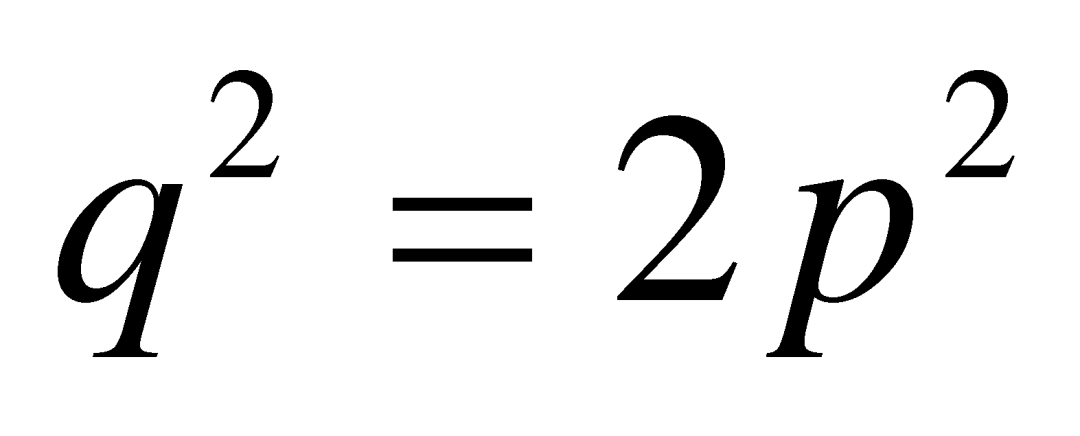 。注意到等式的左边是一个平方数,它只能以0、1、4、5、6、9结尾;等式的右边是一个平方数的两倍,它的末位则只可能是0、2、8。然而q2和2_p_2是相等的,因此它们必须都以0结尾。这说明,p2和q2里一定都含有因子5,从而p和q本身也都含有因子5,这说明
。注意到等式的左边是一个平方数,它只能以0、1、4、5、6、9结尾;等式的右边是一个平方数的两倍,它的末位则只可能是0、2、8。然而q2和2_p_2是相等的,因此它们必须都以0结尾。这说明,p2和q2里一定都含有因子5,从而p和q本身也都含有因子5,这说明![]() 可以继续约分,与假设矛盾。
可以继续约分,与假设矛盾。
我们还有一些更帅的方法来证明,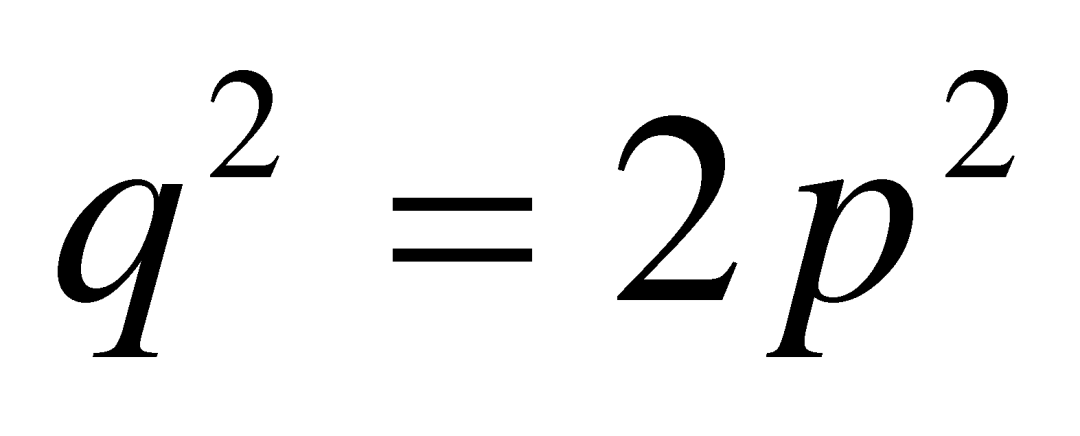 没有正整数解。比方说,注意到,如果对一个平方数分解质因数,它必然有偶数个质因数(
没有正整数解。比方说,注意到,如果对一个平方数分解质因数,它必然有偶数个质因数(![]() 的所有质因数就是把
的所有质因数就是把![]() 的质因数复制成两份)。于是,
的质因数复制成两份)。于是,![]() 有偶数个质因数,
有偶数个质因数,![]() 也有偶数个质因数,
也有偶数个质因数,![]() 就有奇数个质因数。等号左边的数有偶数个质因数,等号右边的数有奇数个质因数,这显然是不可能的,因为同一个数只有一种分解质因数的方法。
就有奇数个质因数。等号左边的数有偶数个质因数,等号右边的数有奇数个质因数,这显然是不可能的,因为同一个数只有一种分解质因数的方法。
无理数的出现推翻了古希腊数学体系中的一个最基本的假设,冲击了古希腊哲学中离散的世界观,引发了数学史上的第一次数学危机。
无理数虽说“无理”,但在生产生活中的用途却相当广泛。量一量你手边的书本杂志的长与宽,你会发现它们的比值都约为1.414。这是因为通常印刷用的纸张都满足这么一个性质:把两条较短边对折到一起,得到一个新的矩形,则新矩形的长宽之比和原来一样。因此,如果原来的长宽比为![]() ,新的长宽比就是
,新的长宽比就是![]() 。解方程
。解方程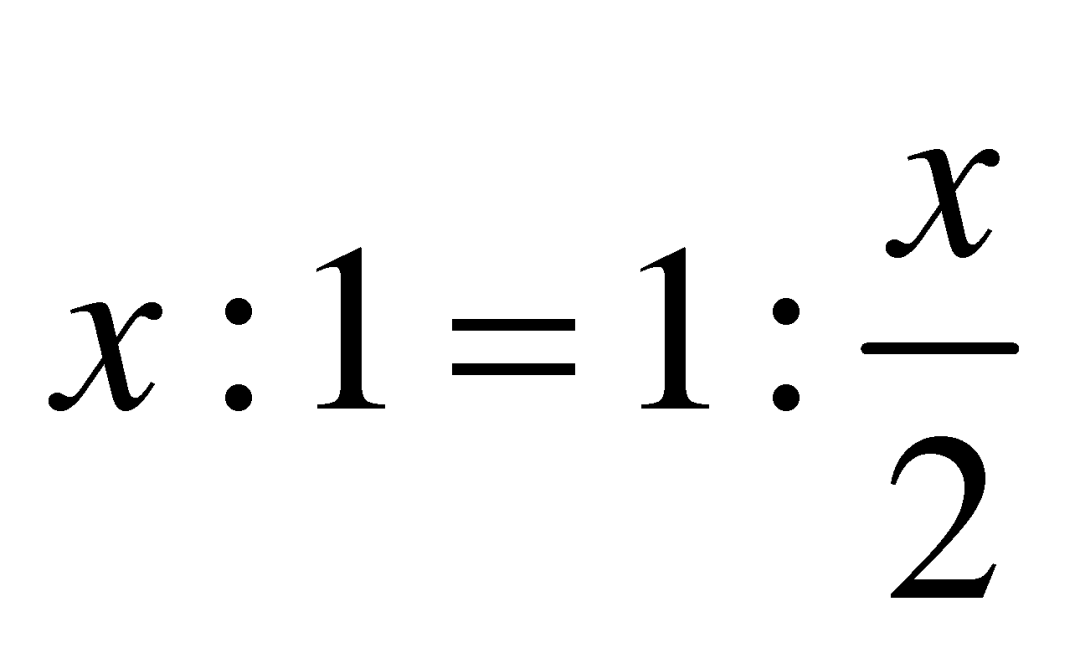 就能得到
就能得到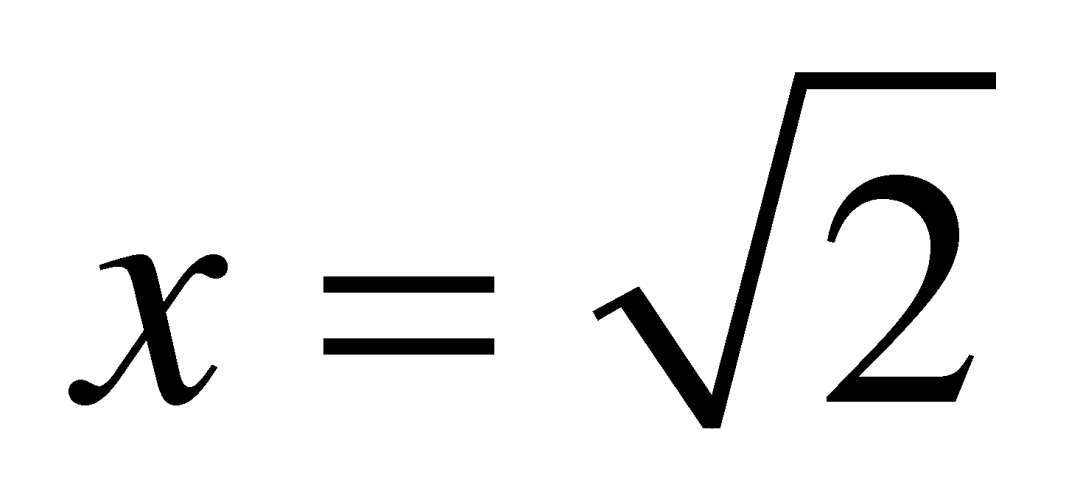 。
。
02
圆周率
不管圆有多大,它的周长与直径的比值总是一个固定的数。我们就把这个数叫做圆周率,用希腊字母![]() 来表示。人们很早就认识到了圆周率的存在,对圆周率的研究甚至可以追溯到公元前。从那以后,人类对圆周率的探索就从未停止过。几千年过去了,人类对圆周率的了解越来越多,但却一直被圆周率是否有理的问题所困扰。直到1761年,德国数学家朗伯(Lambert)才证明了
来表示。人们很早就认识到了圆周率的存在,对圆周率的研究甚至可以追溯到公元前。从那以后,人类对圆周率的探索就从未停止过。几千年过去了,人类对圆周率的了解越来越多,但却一直被圆周率是否有理的问题所困扰。直到1761年,德国数学家朗伯(Lambert)才证明了![]() 是无理数。
是无理数。
![]() 是数学中最基本、最重要、最神奇的常数,它常常出现在一些与几何毫无关系的场合中。例如,全体正整数的平方的倒数和就会收敛到一个与
是数学中最基本、最重要、最神奇的常数,它常常出现在一些与几何毫无关系的场合中。例如,全体正整数的平方的倒数和就会收敛到一个与![]() 有关的数值:
有关的数值:
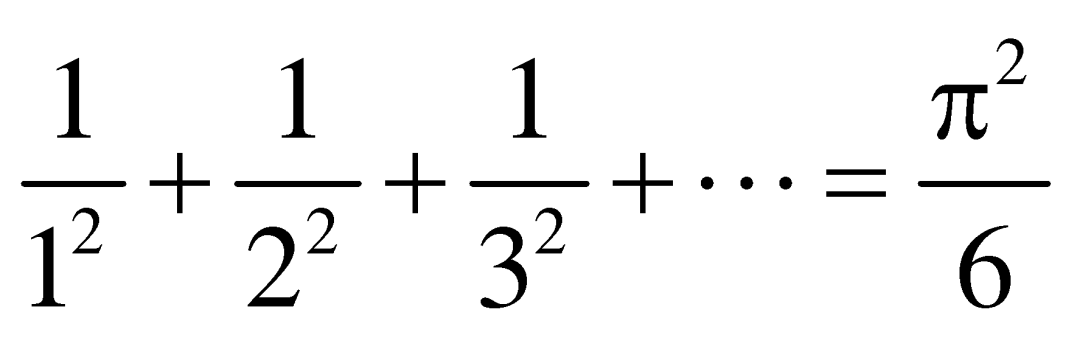
而任意取出两个正整数,则它们互质(最大公约数为1)的概率为![]() ,恰好是上面这个算式答案的倒数。
,恰好是上面这个算式答案的倒数。
03
自然底数
在17世纪末,瑞士数学家伯努利(Bernoulli)注意到了一个有趣的现象:当![]() 越大时,
越大时,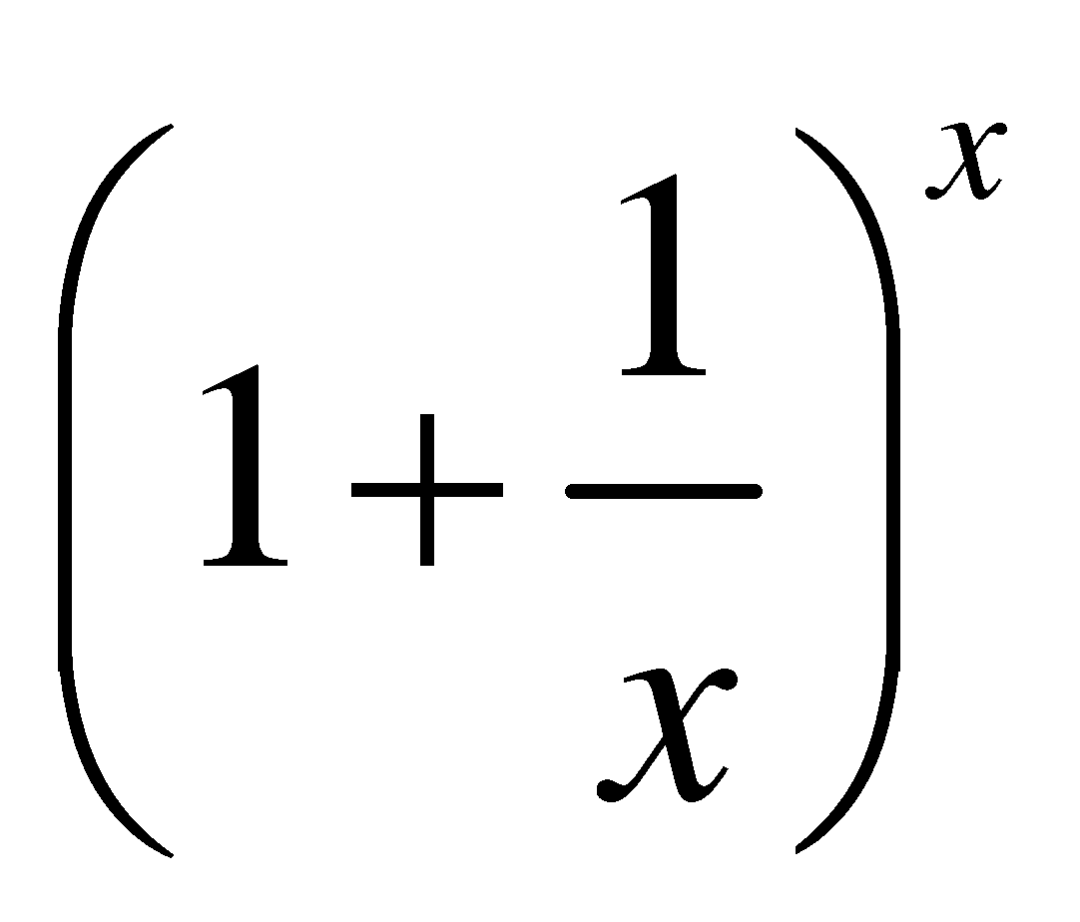 将会越接近某个固定的数:
将会越接近某个固定的数:
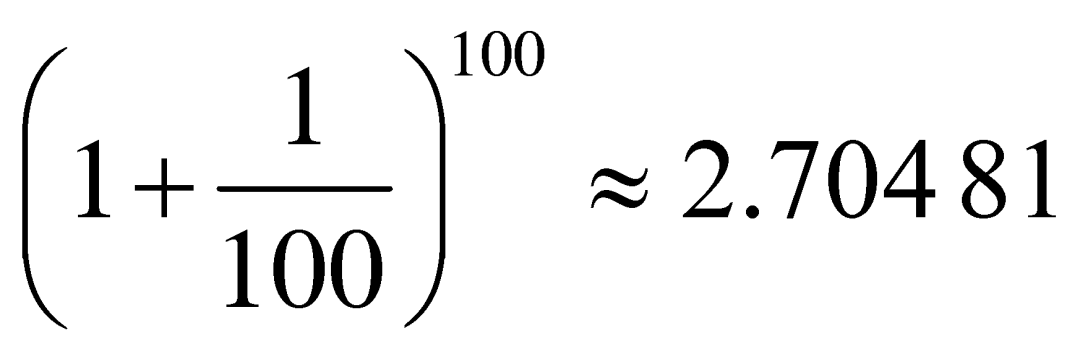
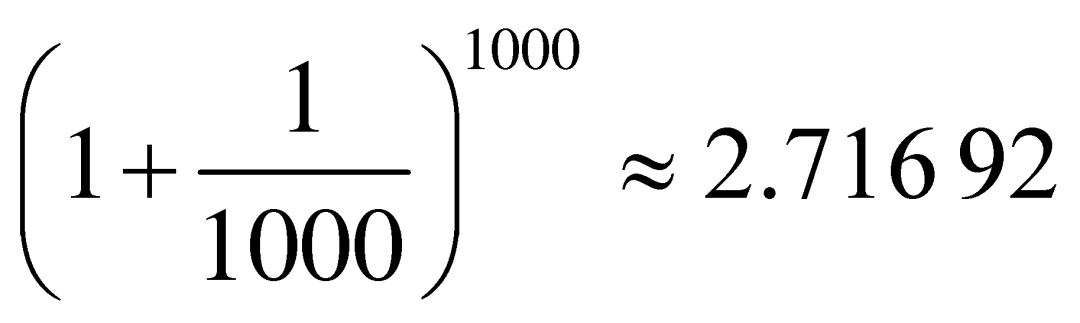
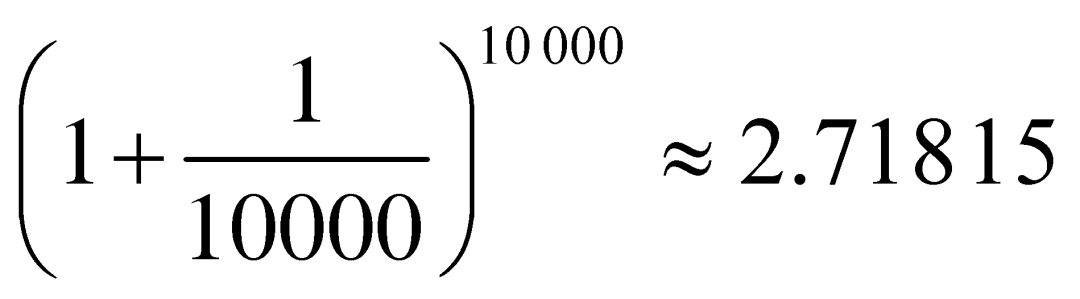
18世纪的大数学家欧拉(Euler)仔细研究了这个问题,并第一次用字母![]() 来表示当
来表示当![]() 无穷大时
无穷大时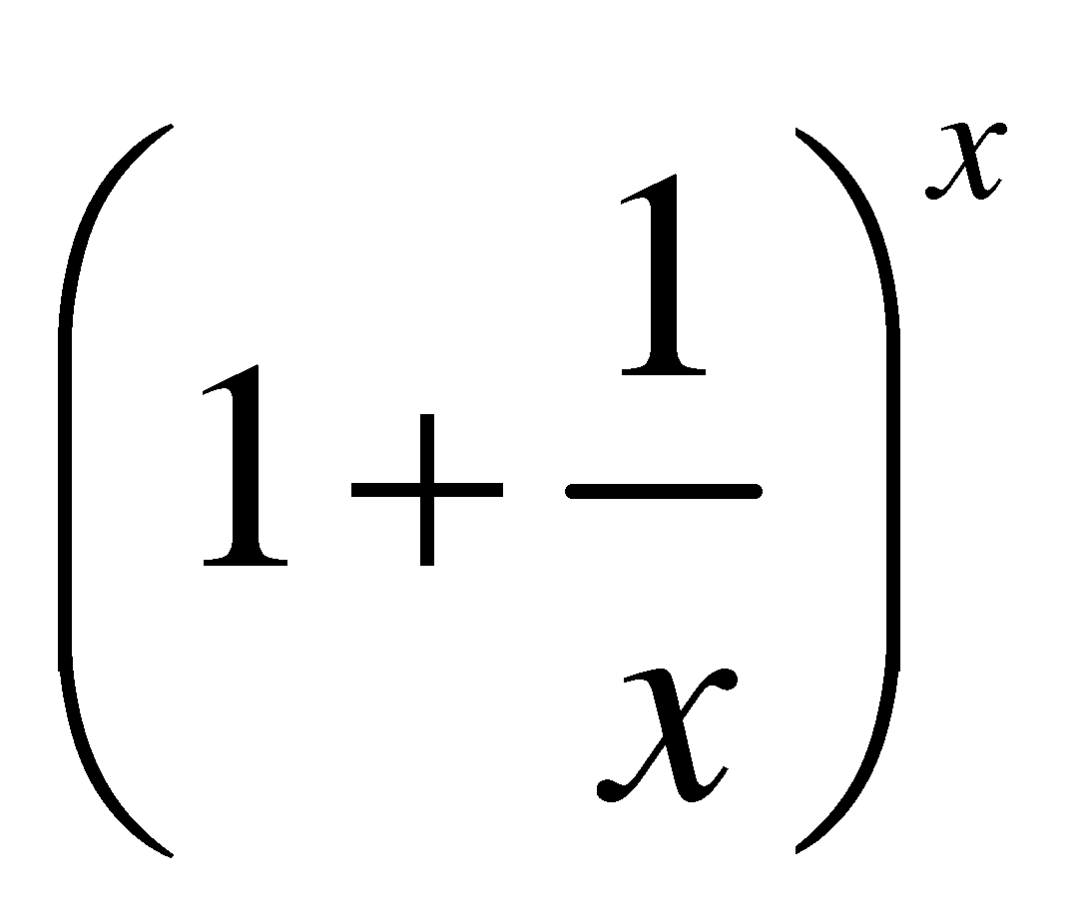 的值。他不但求出了
的值。他不但求出了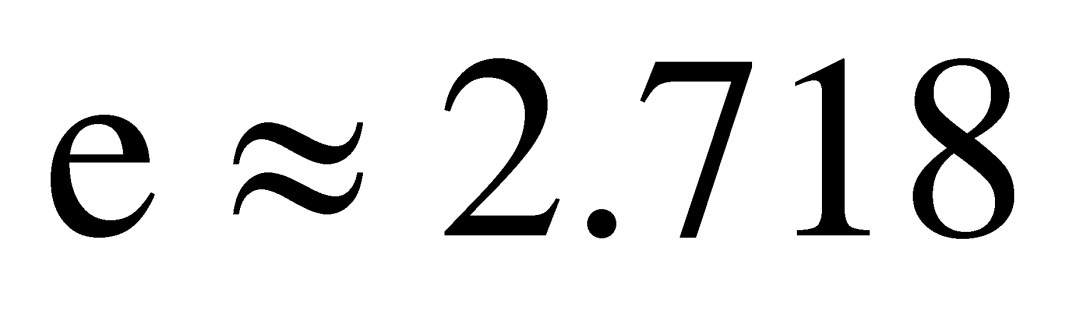 ,还证明了
,还证明了![]() 是无理数。
是无理数。![]() 的用途也十分广泛,很多公式里都有
的用途也十分广泛,很多公式里都有![]() 的身影。比方说,如果把前
的身影。比方说,如果把前![]() 个正整数的乘积记作
个正整数的乘积记作![]() ,则有斯特林(Stirling)近似公式
,则有斯特林(Stirling)近似公式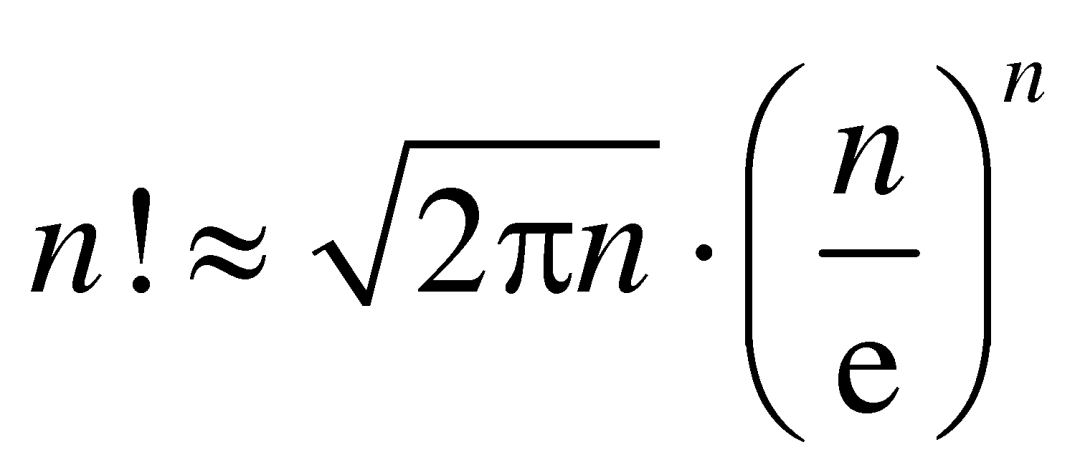 。在微积分中,无理数
。在微积分中,无理数![]() 更是大显神通,
更是大显神通,![]() 的导数竟然是它本身,这使得
的导数竟然是它本身,这使得![]() 也成为了高等数学中最重要的无理数之一。
也成为了高等数学中最重要的无理数之一。
在数学中还有一个奇妙的常数i,它叫做“虚数单位”,简单地说也就是![]() 的意思。虽然
的意思。虽然![]() 看上去非常不合理,但若承认它的存在,所有的n次多项式都会有恰好n个根(包括重根),数系瞬间变得如同水晶球一般完美。可以说,圆周率π、自然底数e和虚数单位i是数学中最基本的三个常数。有一个等式用加法、乘法、乘方这三种最基础的运算,把这三个最基本的常数以及两个最基本的数字(0和1)联系在了一起,没有任何杂质,没有任何冗余,漂亮到了神圣的地步:
看上去非常不合理,但若承认它的存在,所有的n次多项式都会有恰好n个根(包括重根),数系瞬间变得如同水晶球一般完美。可以说,圆周率π、自然底数e和虚数单位i是数学中最基本的三个常数。有一个等式用加法、乘法、乘方这三种最基础的运算,把这三个最基本的常数以及两个最基本的数字(0和1)联系在了一起,没有任何杂质,没有任何冗余,漂亮到了神圣的地步:
eπi + 1 = 0
这个等式也是由欧拉发现的,它叫做“欧拉恒等式”。《数学情报》(The Mathematical Intelligencer)杂志曾举办过一次读者投票活动,欧拉恒等式被评选为“史上最美的公式”。
04
欧拉常数
第一次看到调和级数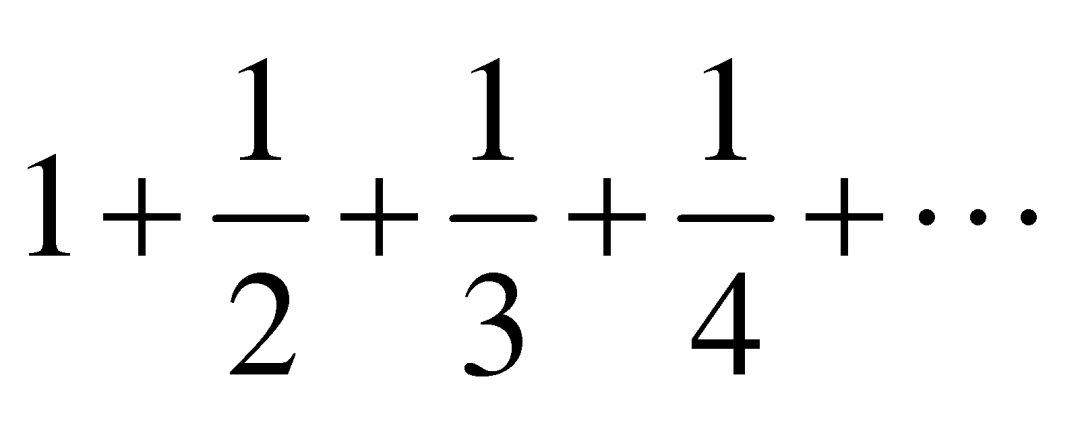 ,很多人都以为它会收敛到一个固定的值。其实,这个级数是发散的,无限地加下去,和也将会变得无穷大。我们很容易证明这一点:把
,很多人都以为它会收敛到一个固定的值。其实,这个级数是发散的,无限地加下去,和也将会变得无穷大。我们很容易证明这一点:把![]() 和
和![]() 都缩小到
都缩小到![]() ,把
,把![]() 到
到![]() 这4个数都缩小到
这4个数都缩小到![]() ,把接下来的8个数都缩小到
,把接下来的8个数都缩小到![]() ,等等,可以看出数列仍然是发散的——因为这相当于有无穷多个
,等等,可以看出数列仍然是发散的——因为这相当于有无穷多个![]() 在相加。因此,我们不但证明了
在相加。因此,我们不但证明了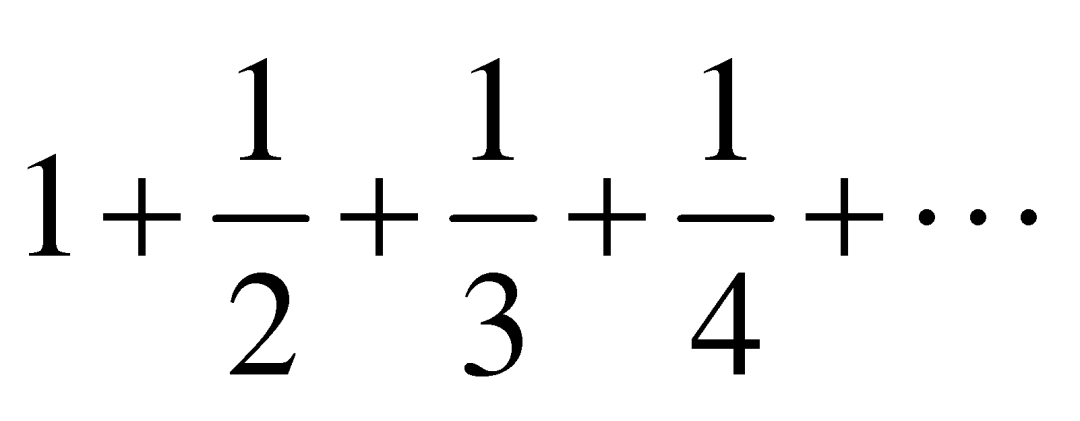 的发散性,还证明了数列的前
的发散性,还证明了数列的前![]() 项之和一定大于
项之和一定大于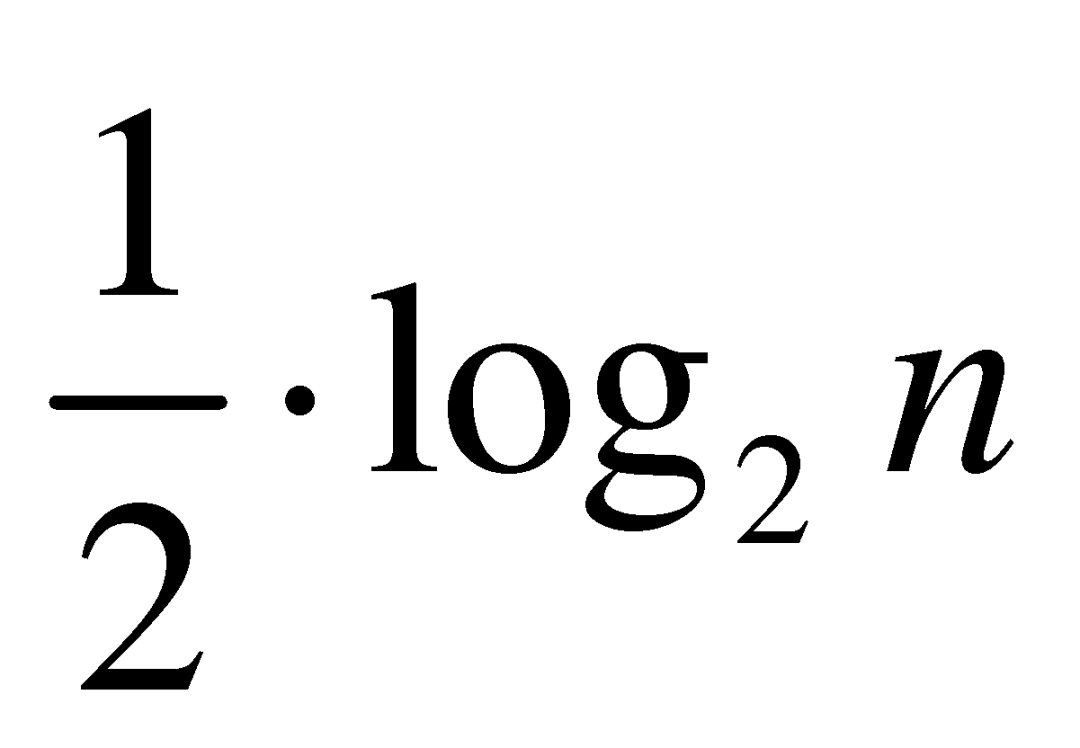 。
。
虽然调和级数是发散的,但它发散的速度非常慢。把![]() 和
和![]() 都放大到
都放大到![]() ,把
,把![]() 到
到![]() 这4个数都放大到
这4个数都放大到![]() ,把接下来的8个数都放大到
,把接下来的8个数都放大到![]() ,等等,可见前
,等等,可见前![]() 项之和不会超过
项之和不会超过![]() 个1相加。按此估算,数列的前1 000 000项之和也不到20。
个1相加。按此估算,数列的前1 000 000项之和也不到20。
注意,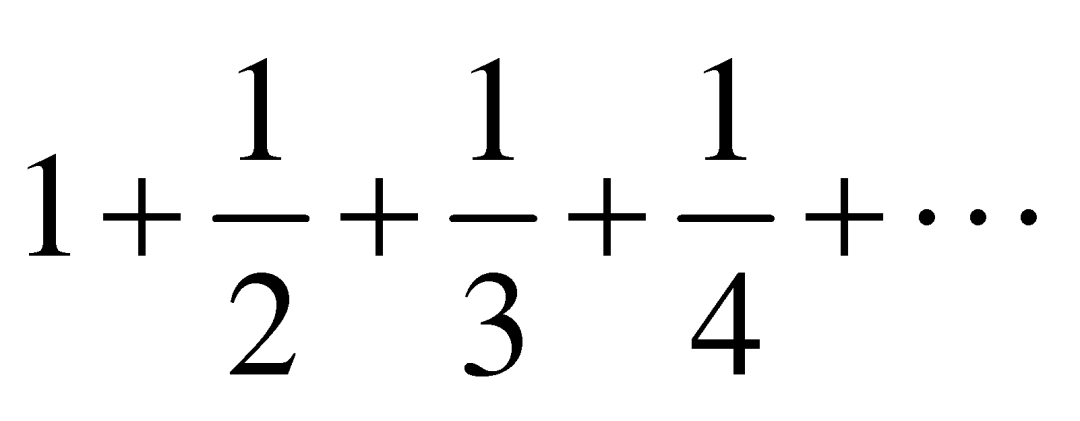 的前
的前![]() 项之和夹在了
项之和夹在了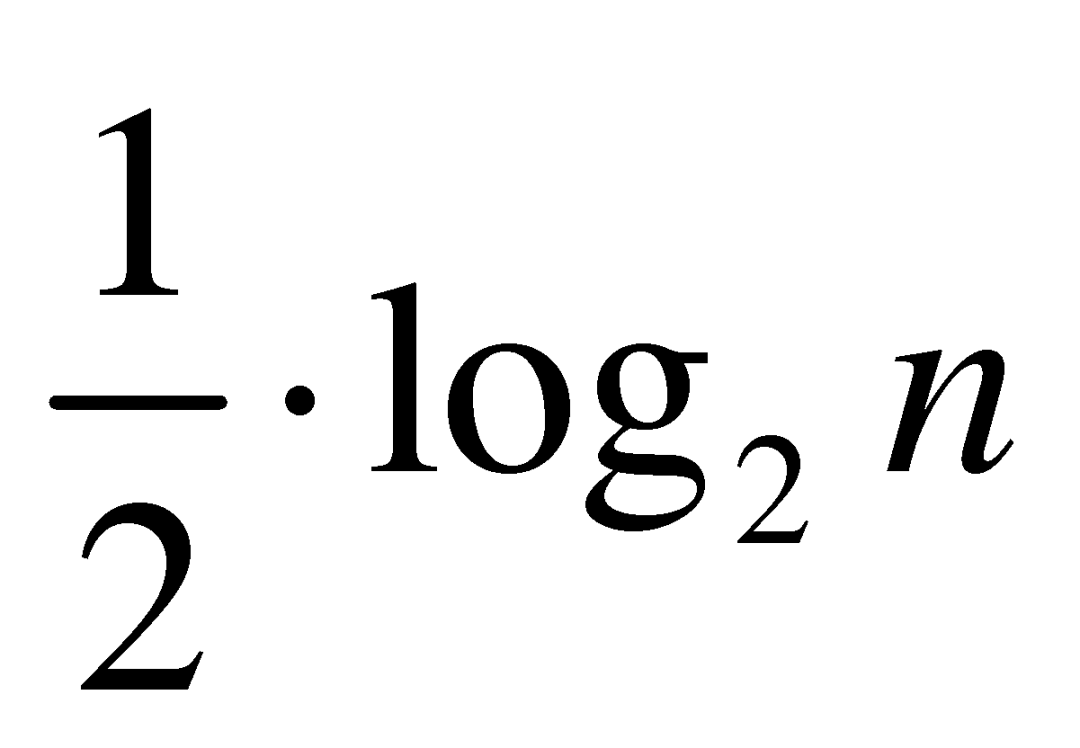 和
和![]() 之间,这表明它一定是对数级增加的。随着
之间,这表明它一定是对数级增加的。随着![]() 的增加,
的增加,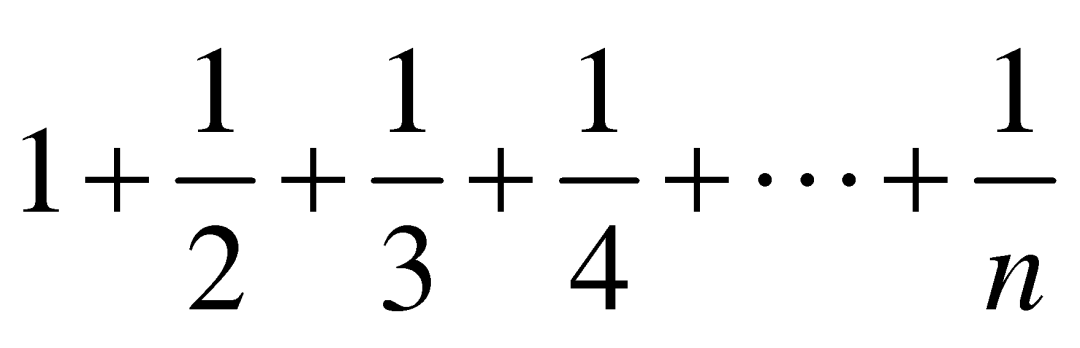 将会越来越接近于
将会越来越接近于![]() 。1735年,欧拉首次发现,当
。1735年,欧拉首次发现,当![]() 增加到无穷大时,
增加到无穷大时,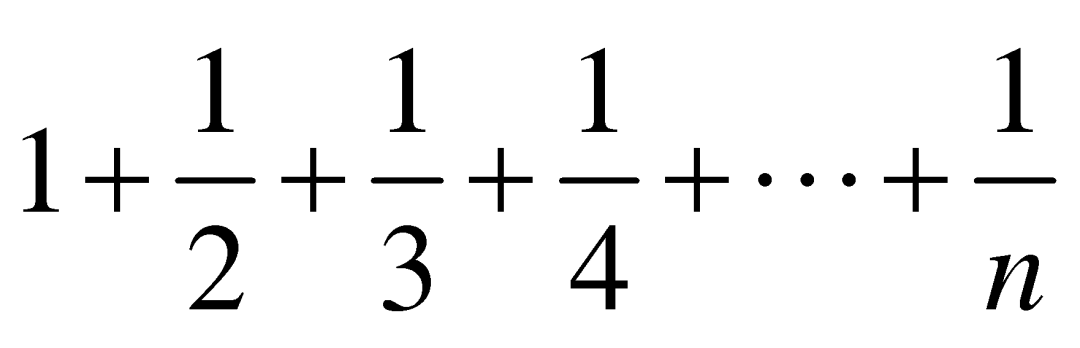 和
和![]() 之间的差将收敛于一个固定的值。这个值就被命名为欧拉常数,用希腊字母
之间的差将收敛于一个固定的值。这个值就被命名为欧拉常数,用希腊字母![]() 来表示,它约等于0.5772。
来表示,它约等于0.5772。
有趣的是,虽然大家都认为欧拉常数一定是无理数,但到目前为止还没有人能够证明这一点。现在已经知道,如果欧拉常数是有理数的话,它的分母至少是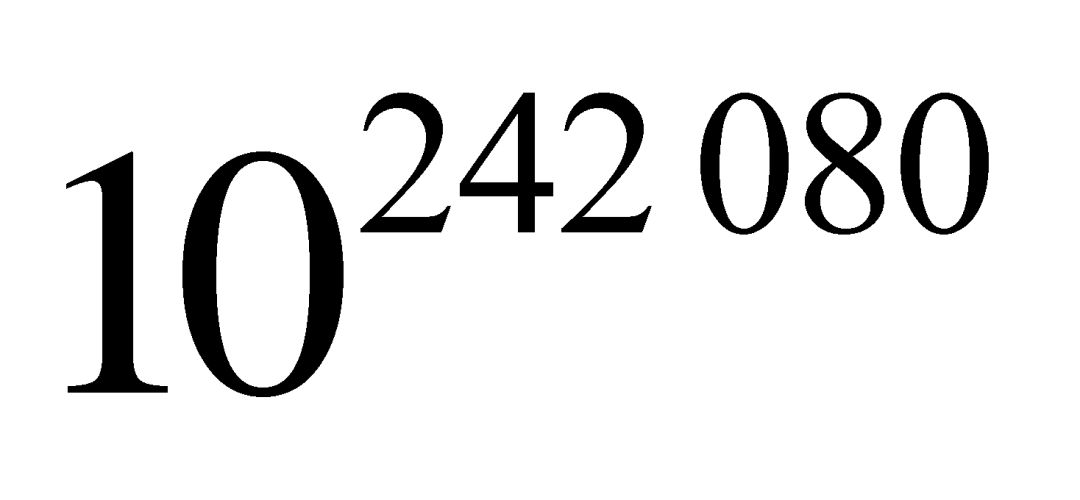 。
。
05
黄金分割
把一条线段分成两段,分割点在什么位置时最为美观?分在中点处,似乎太对称了不好看;分在三等分点处,似乎又显得有些偏了。人们公认,最完美的分割点应该满足这样一种性质:较长段与较短段的长度比,正好等于整条线段与较长段的长度比。这个比值就叫做黄金分割,用希腊字母![]() 来表示。若令线段的较短段的长度为1,则
来表示。若令线段的较短段的长度为1,则![]() 就满足方程
就满足方程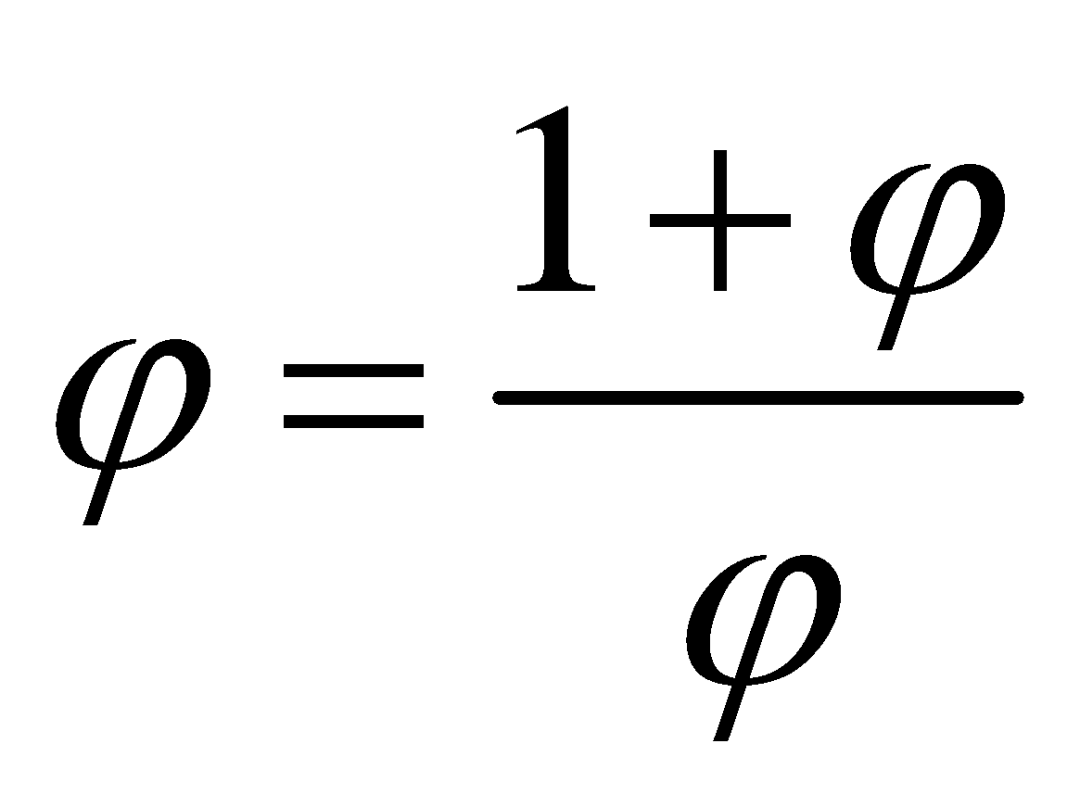 ,可解出
,可解出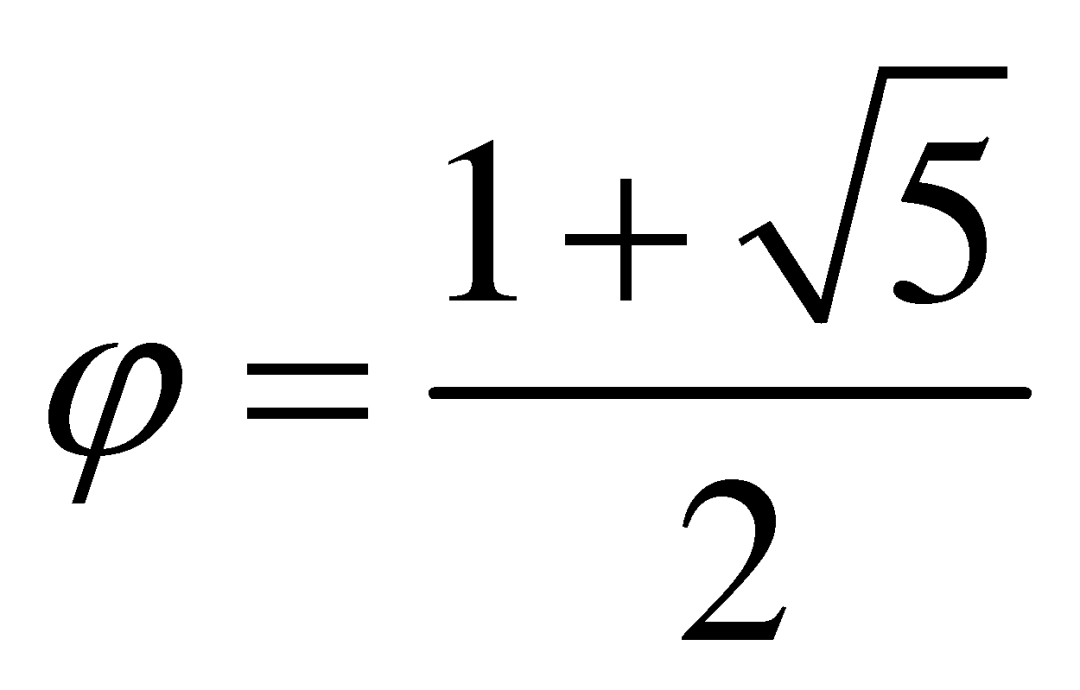 。
。
在美学中,黄金分割有着不可估量的意义。在那些最伟大的美术作品中,每个细节的构图都充分展示了黄金分割之美。在人体中,黄金分割也无处不在——肘关节就是整只手臂的黄金分割点,膝关节就是整条腿的黄金分割点,而肚脐则位于整个人体的黄金分割点处。
在数学中,黄金分割![]() 也展示出了它的无穷魅力。例如,在图1所示的正五角星中,同一条线上三个点A、B、C就满足AB
也展示出了它的无穷魅力。例如,在图1所示的正五角星中,同一条线上三个点A、B、C就满足AB![]() BC=
BC=![]() 。在第12节讲到的8个算术游戏中,
。在第12节讲到的8个算术游戏中,![]() 也出现在了一个出人意料的地方。
也出现在了一个出人意料的地方。

图 1
06
辛钦常数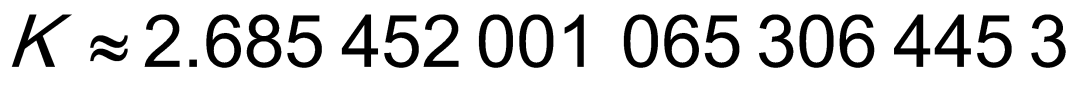
每个实数都能写成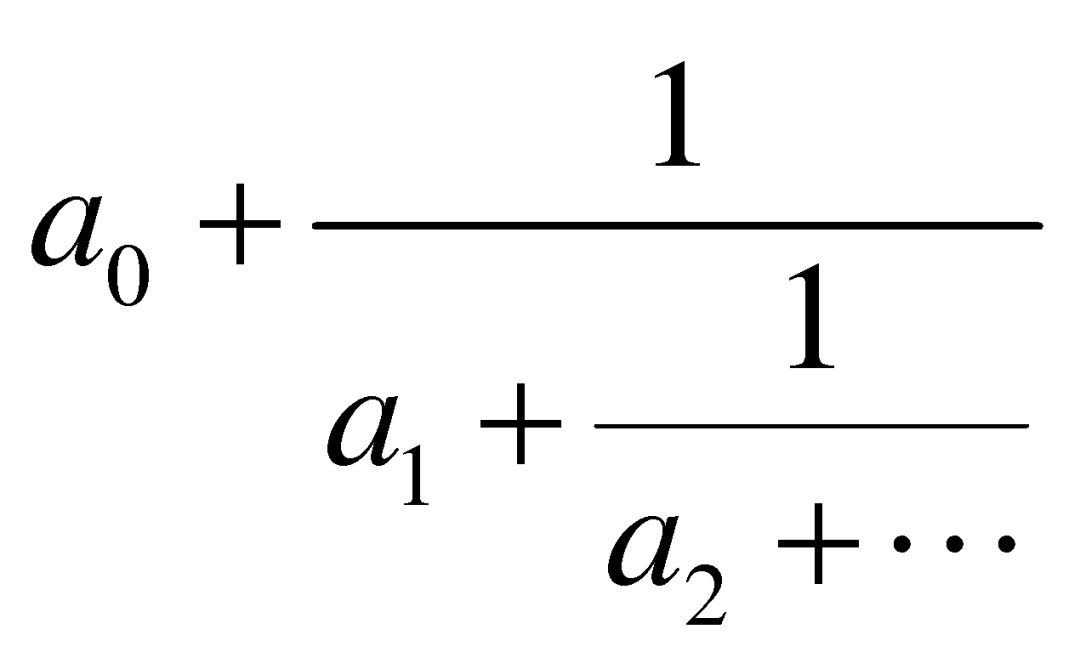 的形式,其中
的形式,其中![]() ,
,![]() ,
,![]() , …都是整数。我们就把
, …都是整数。我们就把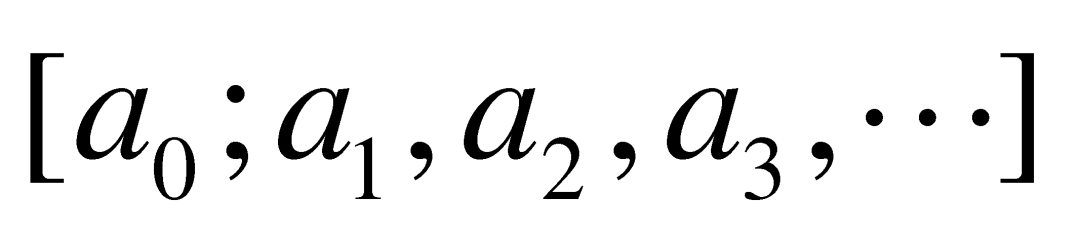 叫做该数的连分数展开。比方说,
叫做该数的连分数展开。比方说,![]() 是一个比3多一点点的数,大概比3多
是一个比3多一点点的数,大概比3多![]() 吧。但是,这个分母7还不够准确。事实上
吧。但是,这个分母7还不够准确。事实上![]() 是一个小于
是一个小于![]() 但是大于
但是大于![]() 的数,也就是说刚才那个分母应该比7要大一点点,因此
的数,也就是说刚才那个分母应该比7要大一点点,因此![]() 可以表示成
可以表示成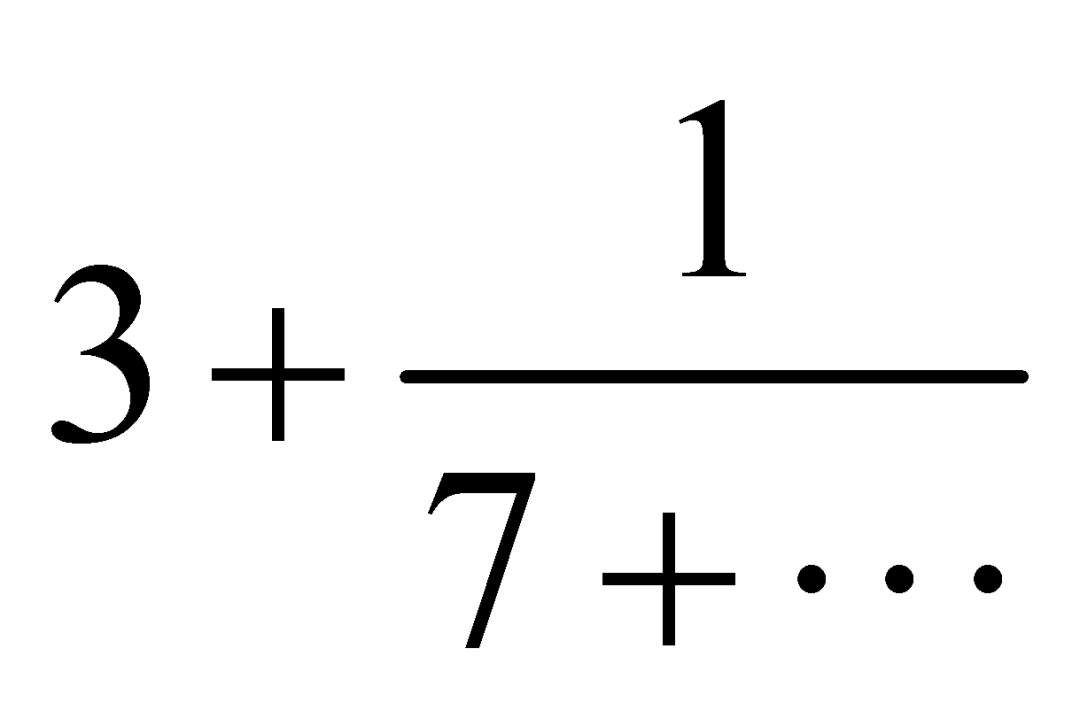 。继续计算我们还能得出更具体的结果,
。继续计算我们还能得出更具体的结果,![]() 约为
约为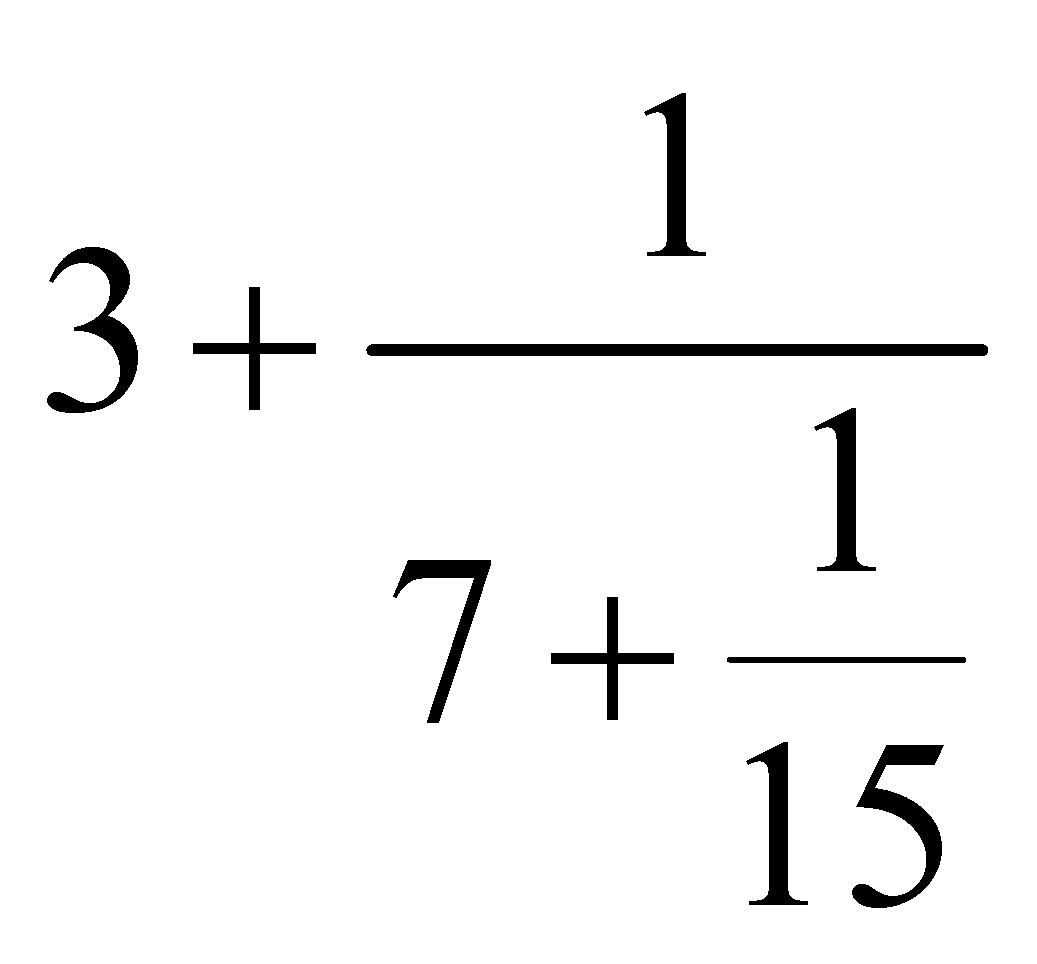 ,但是那个分母15比精确值还稍微小了一些,因此
,但是那个分母15比精确值还稍微小了一些,因此![]() 可以写作
可以写作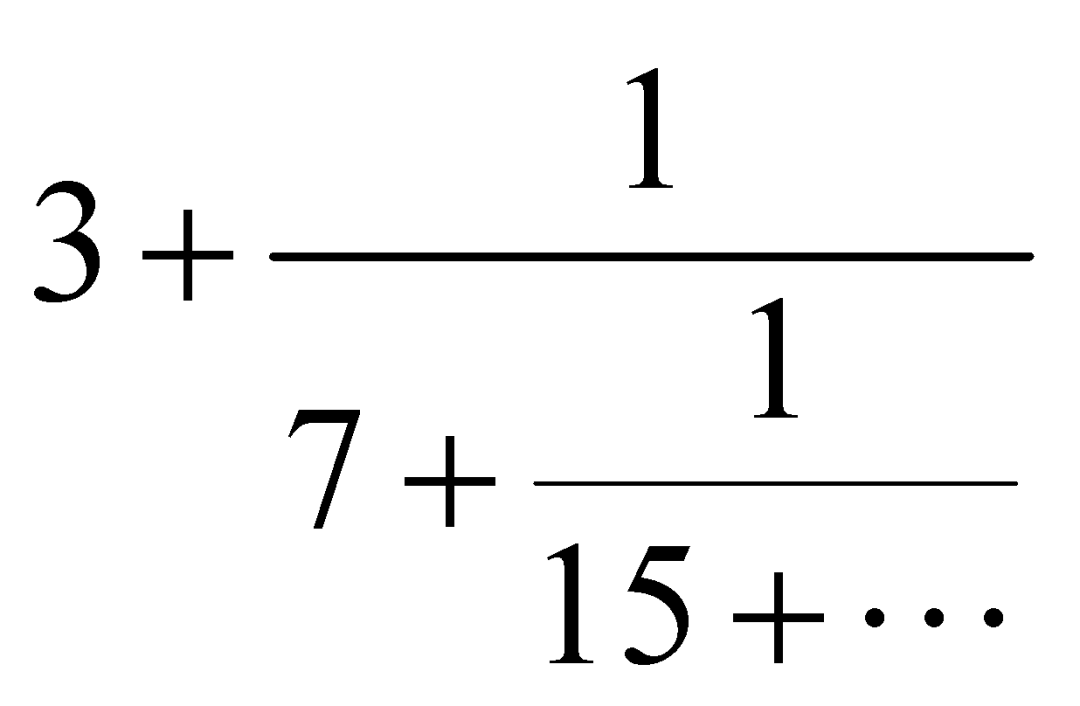 。省略的部分又可以写成多少多少分之一的形式,其中分母又可以拆成一个整数部分加上一个小数部分。不断这样做下去,我们就得到了
。省略的部分又可以写成多少多少分之一的形式,其中分母又可以拆成一个整数部分加上一个小数部分。不断这样做下去,我们就得到了![]() 的连分数展开:
的连分数展开: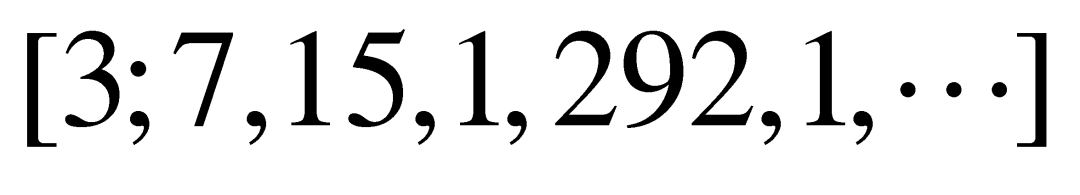 。
。
和小数展开比起来,连分数展开具有更加优雅漂亮的性质,这使得连分数成为了数学研究中的必修课。
在1964年出版的一本连分数数学课本中,数学家辛钦(Khinchin)证明了这样一个惊人的结论:除了有理数和二次整系数方程的根等特殊情况以外,几乎所有实数的连分数展开序列的几何平均数都收敛到一个相同的数,它约为2.685 452。例如,圆周率![]() 的连分数展开序列中,前20个数的几何平均数约为2.628 19,前100个数的几何平均数则为2.694 05,而前1 000 000个数的几何平均数则为2.684 47。
的连分数展开序列中,前20个数的几何平均数约为2.628 19,前100个数的几何平均数则为2.694 05,而前1 000 000个数的几何平均数则为2.684 47。
目前,人们对这个神秘常数的了解并不太多。虽然辛钦常数很可能是无理数,但这一点至今仍未被证明。而辛钦常数的精确值也并不容易求出。1997年,戴维•贝利(David Bailey)等人对一个收敛极快的数列进行了优化,但也只求出了辛钦常数的小数点后7350位。
07
康威常数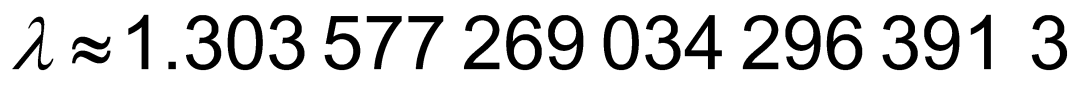
你能找出下面这个数列的规律吗?
1,
11,
21,
1211,
111221,
312211,
13112221,
1113213211,
…
这个数列的规律简单而又有趣。数列中的第一个数是1。从第二个数开始,每个数都是对前一个数的描述:第二个数11就表示它的前一个数是“1个1”,第三个数21就表示它的前一个数是“2个1”,第四个数1211就表示它的前一个数是“1个2,1个1”……这个有趣的数列就叫做“外观数列”(look-and-say sequence)。
外观数列有很多有趣的性质。例如,数列中的数虽然会越来越长,但数字4永远不会出现。1987年,约翰•康威发现,在这个数列中,相邻两数的长度之比越来越接近一个固定的数。最终,数列的长度增长率将稳定在一个约为1.303 577的常数上。康威把这个常数命名为康威常数,并用希腊字母![]() 表示。康威证明了
表示。康威证明了![]() 是无理数,它是某个71次方程的唯一实数解。
是无理数,它是某个71次方程的唯一实数解。
08
钱珀瑙恩常数
把全体正整数从小到大依次写成一排,并在最前面加上小数点,便得到了一个无限小数0.1234567891011121314…。这个数是由英国统计学家钱珀瑙恩(Champernowne)于1933年构造出来的,他把它命名为钱珀瑙恩常数,用符号![]() 表示。与其他的数学常数相比,钱珀瑙恩常数有一个很大的不同之处:这个数仅仅是为了论证一些数学问题而人为定义出来的,它并未描述任何一个数学对象。
表示。与其他的数学常数相比,钱珀瑙恩常数有一个很大的不同之处:这个数仅仅是为了论证一些数学问题而人为定义出来的,它并未描述任何一个数学对象。
钱珀瑙恩常数有很多难能可贵的性质。首先,容易看出它是一个无限不循环小数,因此它也就是一个无理数。其次,它还是一个“超越数”,意即它不是任何一个整系数多项式方程的解。它还是一个“正规数”,意即每一种数字或者数字组合出现的机会都是均等的。在众多数学领域中,钱珀瑙恩常数都表现出了其非凡的意义。
推荐阅读

《思考的乐趣:Matrix67数学笔记》
作者:顾森
本书是一个疯狂数学爱好者的数学笔记,面向所有喜爱数学的读者。本书包括5部分内容,即生活中的数学、数学之美、几何的大厦、精妙的证明、思维的尺度,涉及48篇精彩的文章。即使你不喜欢数学,也会为本书的精彩所倾倒。
这是一本标新立异的趣味数学书。每一个读过的人都会被深深吸引。这是一个热爱思考的年轻人积攒的让人一读就欲罢不能的趣味书。
01

《数学的雨伞下:理解世界的乐趣》
作者:[法] 米卡埃尔•洛奈(Mickaël Launay)
译者:欧瑜
惊讶!是思考的起点;
数学,是理解世界本质与万物关联的工具!
以数学为起点,以思考为快乐!
法国数学学会“达朗贝尔奖”得主科普名作。
数学,是理解世界本质与万物关联的工具,它能制造两个指南针:一个叫“实用”,一个叫“优雅”。不懂得数学的意义,就无法真正学习和理解数学。
科学家为什么那么聪明?因为他们有非凡的思考方法。
以数学为工具,以思考为快乐;培养自己的思考力、观察力,成为真正的思考者。
02

《数学与生活》(1、2、3、4)
作者:远山启
译者:吕砚山、莫德举等
日本学教育议会创立者远山启力作,通俗讲解消除"应试数学"带来给初中数学高中数学带来的恐惧感,了解什么是数学,充分感受数学之美,培养理科逻辑思维。
《数学与生活》为日本数学教育改革之作,旨在还原被考试扭曲的数学,为读者呈现数学的真正容颜,消除应试教学模式带来的数学恐惧感。
























 125
125

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








