
数学是科学的皇后,而数论则是数学的皇后。
——卡尔·弗里德里希·高斯
来源 | 《不可能的几何挑战:数学求索两千年》
作者 |[美] 大卫•S. 里奇森(David S. Richeson)
译者 | 姜喆
认为所有伟大数学家都曾是天才儿童的观点是荒诞的。在数学领域有很多大器晚成的人。但卡尔·弗里德里希·高斯不是其中之一。他的数学天分在年轻时就展露无遗。在他的黄金时代,高斯喜欢讲述这段经历:他的老师让班上所有人去计算算术级数的和,好让学生们有事可做,不会惹麻烦。这位年轻的天才推导出了这种级数的求和公式,然后马上拿着石板告诉老师他已经做完了:“Ligget se.(答案就在这里。)”但他早期的数学尝试不仅限于给老师留下深刻印象,他还是青少年时就得到了很多重大的数学发现——其中之一是我们故事中的一个主要情节。
高斯于 1777 年生于布伦瑞克,那里如今属于德国下萨克森州。因为在数学方面早早显露出天赋,他吸引了布伦瑞克公爵的注意。公爵开始授予高斯奖学金。这让高斯得以前往布伦瑞克卡罗琳学院,以及后来到哥廷根大学就读。高斯没有拿到毕业证书就离开了哥廷根,但他在那里发现了许多重要的数学成果。他从黑尔姆施泰特大学取得了博士学位。
公爵继续发给高斯津贴,这样后者就能把所有时间都投入研究中。但后来,公爵在为普鲁士军队作战时牺牲,就没有人再支付这笔钱了。因为需要工作,高斯接受了新哥廷根天文台台长的职位。他直到老年时期还在继续研究,最终于 1855 年在哥廷根过世。
不像持续发表文章的欧拉,高斯是一位完美主义者。他会暂时保留自己的发现,不断打磨,直到能发表一篇杰作出来。这些发现在被发表时一定十分成熟、极其深刻,并且令其他人难以理解;数学界经常要花上数年才能完全理解高斯的想法。高斯个人的座右铭用在这里恰如其分:宁可少些,但要好些(pauca sed matura)。数学家们不断地从高斯本人或是他留下的笔记中了解到,即便是数十年甚至数世纪之后的新数学发现,都有可能只是重新发现了高斯早已得到的某个想法。
高斯的研究领域过于广泛,我们无法一一描述。他为代数、分析、数论、几何、拓扑学、复分析、线性代数、统计学以及物理和天文学的很多领域都做出了重要贡献。
十七边形
1796 年,高斯开始记录他的第一篇数学日记。在头一年,它只是记载了高斯那一年的数学成就和发现(共 49 篇)。尽管很多记述晦涩难解(不只对于我们,显然对于晚年的高斯也是一样的),标注日期为 1796 年 3 月 30 日的第一篇日记却很清楚明白:
此时,除了这一句话以外,高斯什么都没写。就在离他 19 岁生日还有一个月的时候,这位青年发现了可以仅用尺规作正十七边形。不仅如此,他还给出了可作图正多边形的一般规则。同年晚些时候,他写道:
看上去,自从欧几里得的时代以来,人们就说服自己,初等几何的知识范畴已经无法再被扩展;至少我不知道任何在这一问题上扩展边界的成功尝试。那么在我看来,下述事实就更加非同寻常了:除了通常的多边形,还存在一些其他的可以几何作图的多边形,例如十七边形。
他继续写道:“这一发现只是一个尚未完成的更大发现的推论。一旦完成,我就会公之于众。”他确实还有更多东西要说。该发现后来成了高斯在 1801 年出版的《算术研究》中的一部分。该书是数论领域的一本杰出论述。
奥拉夫·诺伊曼这样评论《算术研究》:“它迅速被当时的专家们认可……为一本杰作。它的条理性、严密性以及内容之丰富都是前所未有的。它把数论从一座座分散的孤岛变成数学中一块正式的大陆……这本书是数学,也是人类文明的‘永恒经典’。”
高斯对多边形可作图性这一发现非常自豪。有些人说正是这一发现激励高斯成为数学家。他还要求把十七边形刻在自己的墓碑上。这一要求最后没能实现,但今天他的家乡布伦瑞克兴建了一座高斯雕像,上面装饰着一个十七角星。
有趣的是,高斯没有给出尺规作十七边形的作图步骤,至少在他出版的书中没有提过。但他证明了这样的作图是可能的。我们知道  是单位圆内接正十七边形的一个顶点的横坐标。高斯只用整数、四则运算以及平方根表示出了
是单位圆内接正十七边形的一个顶点的横坐标。高斯只用整数、四则运算以及平方根表示出了  这个数。根据笛卡儿定理,这个点可以作图,因此十七边形也可以作图。
这个数。根据笛卡儿定理,这个点可以作图,因此十七边形也可以作图。
如今的文献包含很多十七边形作法。1915 年,罗伯特·高登林格写了一本包含超过 20 种十七边形作法的书,但一位评论家指出这“还远称不上完整”。假设我们已知一个以  为圆心的圆,以及圆上两点
为圆心的圆,以及圆上两点  、
、 ,并且
,并且  是直角(图 19.1)。令点
是直角(图 19.1)。令点  到
到  的距离是
的距离是  长度的 1/4。连接线段
长度的 1/4。连接线段  。在
。在  上找一点
上找一点  ,使得
,使得  。在
。在  上找一点
上找一点  ,使得
,使得  。现在以
。现在以  为直径作一个圆,交
为直径作一个圆,交  于点
于点  。以
。以  为圆心、以
为圆心、以  为半径作圆,交
为半径作圆,交  于
于  和
和  。经过
。经过  和
和  并且垂直于
并且垂直于  的直线与圆交于 4 个点。这些点就是十七边形的 4 个顶点(
的直线与圆交于 4 个点。这些点就是十七边形的 4 个顶点( 是第五个顶点)。用这 5 个顶点,就能作出剩下的 12 个顶点。
是第五个顶点)。用这 5 个顶点,就能作出剩下的 12 个顶点。
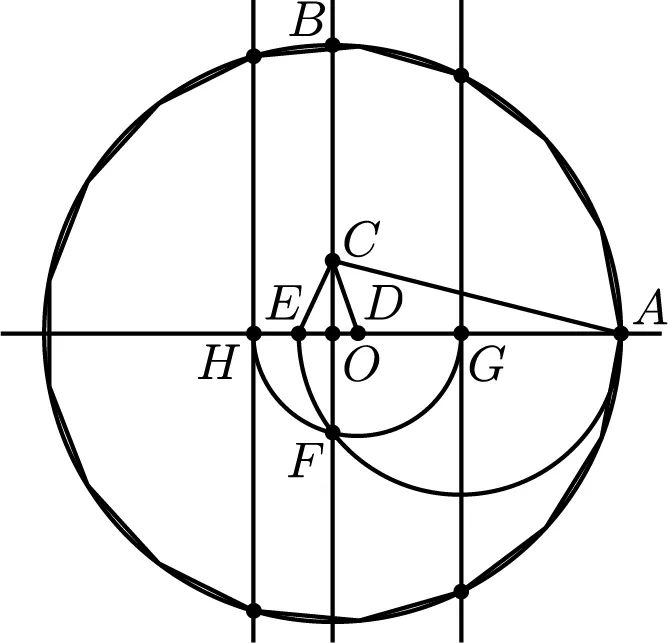
图 19.1 十七边形的一种作法
高斯定理
高斯关于十七边形可作图的证明只是锦上添花。它的确是个容易让我们游行庆祝(或者将它永远地刻在纪念碑上)的结果。但它仅仅是一个优质样品,其背后是一个远更深奥的结果。
回想一下,古希腊人知道如何作等边三角形、正方形和正五边形。利用这些,他们也能作正  边形,只要
边形,只要  形如
形如  、
、 、
、 或
或  。高斯发现了使得正
。高斯发现了使得正  边形可以作图的除了 3 和 5以外的质数
边形可以作图的除了 3 和 5以外的质数  ,例如 17。
,例如 17。
质数 3、5 和 17 有什么特别的呢?结果证明,关键在于  在这三种情况下都是 2 的幂:
在这三种情况下都是 2 的幂: ,
, ,
, 。事实上,就连这三个指数也是 2 的幂:
。事实上,就连这三个指数也是 2 的幂: ,
, ,
, 。我们把形如
。我们把形如  的数称为费马数。如果一个费马数是质数,我们就称它为费马质数。3、5 和 17 之后的两个费马数也是质数:
的数称为费马数。如果一个费马数是质数,我们就称它为费马质数。3、5 和 17 之后的两个费马数也是质数: 和
和  。高斯在《算术研究》中证明了下面这个非凡的定理。
。高斯在《算术研究》中证明了下面这个非凡的定理。
高斯定理:如果  形如
形如  ,其中
,其中  且
且  为不同的费马质数,那么正
为不同的费马质数,那么正  边形可作图。
边形可作图。
高斯定理暗示了正 257 边形(由 F. J. 里切洛特于 1832 年作出)和正 65 537 边形(由林根的赫尔梅斯在经过 10 年的研究之后于大约 1894 年作出)可以作图。同样可以作图的还有 34 边形(34 = 2·17)、51 边形(51 = 3·17)、68 边形( )、69 904 边形(
)、69 904 边形( )等。1000 以内的正
)等。1000 以内的正  边形中至少有 52 个可以作图:3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272, 320, 340, 384, 408, 480, 510, 512, 514, 544, 640, 680, 768, 771, 816 以及 960。
边形中至少有 52 个可以作图:3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272, 320, 340, 384, 408, 480, 510, 512, 514, 544, 640, 680, 768, 771, 816 以及 960。
尽管如此非凡卓越,高斯定理也仅仅部分解决了正多边形可作图性问题。首先,完整的答案至少需要知道哪些费马数是质数。这个问题有一段有趣的历史,我们等一下会来介绍。
与完整答案间更重要的一段差距在于以下问题:如果  不具有上述形式,那么
不具有上述形式,那么  边形是否可以作图?高斯定理没法处理七边形或者九边形——7 不是费马质数,而
边形是否可以作图?高斯定理没法处理七边形或者九边形——7 不是费马质数,而  是费马质数的平方。高斯定理还是保留了这两个图形可以作图的可能性。事实上,它们不可作图。而且根据高斯所述,他知道这一点。他写道,自己可以“十分严谨”地证明高斯定理的逆命题,但他又接着写道:
是费马质数的平方。高斯定理还是保留了这两个图形可以作图的可能性。事实上,它们不可作图。而且根据高斯所述,他知道这一点。他写道,自己可以“十分严谨”地证明高斯定理的逆命题,但他又接着写道:
当前工作的局限性让我必须先在这里放弃这个证明,但我们要提出警告,免得有人尝试我们的理论没有给出的分割(例如,分为 7, 11, 13, 19 …份等),因而浪费时间。
这句话换种说法就是:“在这里给出证明并不值得。但相信我,我知道剩下的那些都不可作图。别浪费时间去尝试了。”皮埃尔·汪策尔在 1837 年给出了这一问题的严格证明(我们会在第 20 章更详细地介绍这一点)。
把高斯和汪策尔的定理合在一起,我们会得到一个新的结果。
高斯–汪策尔定理:当且仅当  ,其中
,其中  且
且  为不同的费马质数时,正
为不同的费马质数时,正  边形可作图。
边形可作图。
费马质数
感谢高斯–汪策尔定理,我们可以知道究竟哪些正多边形可以用尺规作图——至少在理论上。在实践中,我们需要知道哪些费马数是质数。而这还是一个悬而未决的问题。
对该问题的研究可以追溯到 17 世纪前半叶。费马发现当 j=0,1,2,3,4 时, 是质数(3、5、17、257 以及 65 537)。他猜想所有这样的数都是质数。在 1640 年写给贝尔纳·弗雷尼可·德·贝西的一封信中,费马列出了前七个费马数(第七个有 20 位数字)并写道:
是质数(3、5、17、257 以及 65 537)。他猜想所有这样的数都是质数。在 1640 年写给贝尔纳·弗雷尼可·德·贝西的一封信中,费马列出了前七个费马数(第七个有 20 位数字)并写道:
我还没能证明,但我已经通过绝对可靠的证明排除了很多因数。直觉是我思考的基础,而我产生了强烈的直觉,那就是我很难撤回这一猜想。
费马在 17 世纪四五十年代不断地重新研究这些数。在和数学家们的通信中,他总是主张这是一个质数序列,但他也承认无法证明这一点。如果这是正确的,那它就会是一个伟大的定理。从古希腊时代,我们就知道存在无穷多质数。但我们始终没有一个生成质数的方法。而费马的公式带来了质数生成函数的希望。
这一猜想在随后的半个多世纪都未能得到证明。随后,22 岁的欧拉加入了进来。他当时刚刚接受了位于新兴城市圣彼得堡的科学院的新工作,正在安顿下来。当时刚刚从圣彼得堡搬到莫斯科去指导彼得二世的克里斯蒂安·哥德巴赫,也从这时开始了与欧拉之间长达 30 年的包括将近 200 封信件的书信往来。
1729 年 12 月 1 日,在他给欧拉的第一封信的附言中,哥德巴赫提到了费马问题:
又及:费马发现所有形如  的数,也就是 3、5、17 等,都是质数。他自己承认无法证明,而就我所知,也没有任何人证明了这一发现。
的数,也就是 3、5、17 等,都是质数。他自己承认无法证明,而就我所知,也没有任何人证明了这一发现。
欧拉起初对这个问题不感兴趣,但哥德巴赫一直刺激他。欧拉终于提起了兴趣,把注意力转向了费马序列。1732 年 9 月 26 日,欧拉向圣彼得堡学院提出了结论:费马猜想是错误的。在补充文章中,他写道:
但我不知道出于怎样的命运,结果证明这序列中紧接着的一个数, ,就不再是质数了;我在思考了很多天之后,发现这个数可以被 641 整除,任何想要检查的人立刻就能验证这一点。
,就不再是质数了;我在思考了很多天之后,发现这个数可以被 641 整除,任何想要检查的人立刻就能验证这一点。
通过证明  存在因数 641 和 6 700 417,欧拉让费马找到质数序列的愿望破灭了。欧拉是怎么找到这两个因数的?暴力查找并不是没有可能。尽管
存在因数 641 和 6 700 417,欧拉让费马找到质数序列的愿望破灭了。欧拉是怎么找到这两个因数的?暴力查找并不是没有可能。尽管  有大约 6500 个可能的质因数,如果我们从 2、3、5 开始一个个检查,只要尝试 116 次就能找到一个因数。〔事实上,当八岁的“人形计算器”齐拉·科尔伯恩(1804—1840)在全美巡回展示自己的心算能力时,“有人向这个孩子提出了这个数(
有大约 6500 个可能的质因数,如果我们从 2、3、5 开始一个个检查,只要尝试 116 次就能找到一个因数。〔事实上,当八岁的“人形计算器”齐拉·科尔伯恩(1804—1840)在全美巡回展示自己的心算能力时,“有人向这个孩子提出了这个数( ),而他仅靠心算就找到了因数”。〕这当然不是欧拉所用的方法。
),而他仅靠心算就找到了因数”。〕这当然不是欧拉所用的方法。
欧拉在第一篇文章中没有解释自己怎样得到了这一因数分解。但 15 年后,在另一篇文章中,他解释了他是如何找到 641 的。欧拉使用了“费马小定理”。费马不加证明地提出了这一定理,而证明最终由欧拉在 1736 年完成。欧拉用这一定理证明了对于整数  ,如果
,如果  存在质因数,那它一定形如
存在质因数,那它一定形如  ,其中
,其中  为整数。因此,欧拉只需要检查形如
为整数。因此,欧拉只需要检查形如  的质数。前九个具有如此形式的数中有四个是质数——193、257、449 和 557——但它们都不能整除
的质数。前九个具有如此形式的数中有四个是质数——193、257、449 和 557——但它们都不能整除  。而第十个数就让欧拉获得了成功:64·10 + 1 = 641。
。而第十个数就让欧拉获得了成功:64·10 + 1 = 641。
费马没能因数分解  有些令人惊讶,因为他曾用与欧拉的方法非常类似的技巧分解
有些令人惊讶,因为他曾用与欧拉的方法非常类似的技巧分解  。但正如安德烈·韦伊(1906—1998)所写:“我们能想象到,当(费马)第一次想到这个猜想时,他被自己的热忱冲昏了头脑,犯了个数值错误,再也没有检查过他的计算过程。”
。但正如安德烈·韦伊(1906—1998)所写:“我们能想象到,当(费马)第一次想到这个猜想时,他被自己的热忱冲昏了头脑,犯了个数值错误,再也没有检查过他的计算过程。”
费马发现前五个费马质数之后的 370 年间,我们没有再发现新的费马质数。目前,我们知道接下来的 28 个费马数都是合数。有 25 亿位数字的巨数

是第一个素性未知的费马数。
单位根和正多边形
我们在讨论高斯定理的证明前,要先回一趟复数的王国。我们先来看一个看起来很简单的问题: 是多少?是 1,对吧?当然对。如果我们求 1 的四次方,那么结果还是 1。不过,1 不是 1 唯一的四次方根。它还有三个四次方根:-1、i 以及 - i。因为
是多少?是 1,对吧?当然对。如果我们求 1 的四次方,那么结果还是 1。不过,1 不是 1 唯一的四次方根。它还有三个四次方根:-1、i 以及 - i。因为  。一般来说,
。一般来说, 次单位根指的是方程
次单位根指的是方程  的任意复数解。四次单位根一共有四个:1、-1、i 以及 - i。
的任意复数解。四次单位根一共有四个:1、-1、i 以及 - i。
如图 19.2 所示,四次单位根是复平面内单位圆内接正方形的四个顶点。尽管麻烦,但也不难验证 ±1、 是六个六次单位根。它们是单位圆内接正六边形的顶点。所以,圆内接正
是六个六次单位根。它们是单位圆内接正六边形的顶点。所以,圆内接正  边形问题和
边形问题和  次单位根的值紧密相关——单位根就是多边形的顶点。
次单位根的值紧密相关——单位根就是多边形的顶点。
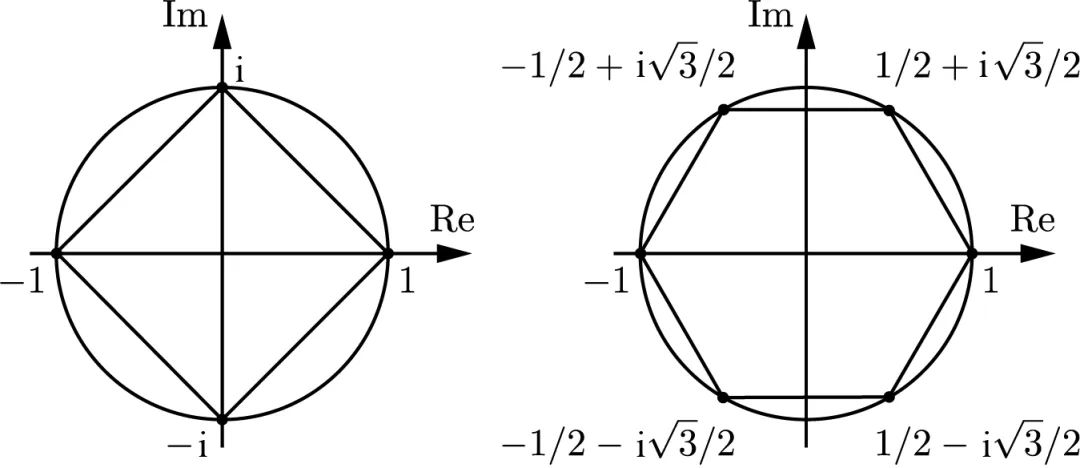
图 19.2 单位根构成了正多边形
我们可以用欧拉公式来验证这一断言。假设  是
是  次单位根。那么
次单位根。那么  。要使此等式成立,必然有
。要使此等式成立,必然有  。又因为
。又因为  是一个非负实数,所以
是一个非负实数,所以  。所以
。所以  ,因此
,因此  ,
, 。要让这两个等式成立,
。要让这两个等式成立, 需要是 360°(用弧度制表示就是
需要是 360°(用弧度制表示就是  )的整数倍,这等价于
)的整数倍,这等价于  ,其中
,其中  为整数。所以,
为整数。所以, 次单位根就是
次单位根就是  ,其中
,其中  。用这种方式,我们就能看出
。用这种方式,我们就能看出  次单位根其实是单位圆上距离相等的
次单位根其实是单位圆上距离相等的  个点。
个点。
如果  ,我们就会发现六次单位根都是形如
,我们就会发现六次单位根都是形如  的数。比如,当
的数。比如,当  时,我们有
时,我们有  。当
。当  时,我们有
时,我们有  。
。
因此,高斯意识到,要解决多边形问题,必须求得  的根。如果
的根。如果  的实部和虚部能用四则运算和平方根表示,对应的多边形就可以作图。事实上,如果
的实部和虚部能用四则运算和平方根表示,对应的多边形就可以作图。事实上,如果  可以作图,
可以作图, 亦然。
亦然。
高斯不是第一个考察  的数学家。1740 年,欧拉证明对于
的数学家。1740 年,欧拉证明对于  ,方程
,方程  有根式解;也就是说,这个多项式的所有根都能用四则运算加上平方根、立方根、四次方根等表示。1770年,亚历山大–西奥菲尔·范德蒙(1735—1796)证明了
有根式解;也就是说,这个多项式的所有根都能用四则运算加上平方根、立方根、四次方根等表示。1770年,亚历山大–西奥菲尔·范德蒙(1735—1796)证明了  的情况。这些都是重要的数学成果,尤其是事后来看。因为不是所有 5 次或更高次的多项式都有根式解。但它们还是没有回答这些多边形能否作图的问题。为此,我们必须证明这些顶点的表达式只用到了平方根,没有其他次方根。而这正是青年高斯所发现的。
的情况。这些都是重要的数学成果,尤其是事后来看。因为不是所有 5 次或更高次的多项式都有根式解。但它们还是没有回答这些多边形能否作图的问题。为此,我们必须证明这些顶点的表达式只用到了平方根,没有其他次方根。而这正是青年高斯所发现的。
高斯的证明思路
高斯的《算术研究》的第七个部分,也是最后一个部分,专门讨论作正多边形问题。他的证明依赖于数论、方程理论以及复数性质。从一种角度来看,这个证明是关于多边形的可作图性。但实际上,它是对形如  的多项式的研究。
的多项式的研究。
每个数学家都知道并且享受那些美妙的“啊哈”时刻。它们总是出现在最出人意料的时间——淋浴时、开车回家时、遛狗时、吃饭时或者躺在床上时。日复一日、年复一年地专注思考一个貌似难以解决的问题,会让头脑在潜意识中灵光一闪。答案通常都是在放松的时候涌现,就好像是上苍的启示一般。高斯就描述过一次这样的经历:
我当时在布伦瑞克度假。经过努力思考( 的)所有根之间在算术性质上的联系,我在那一天(起床前)成功地看清了这个关系,所以我得以当场把它应用到十七边形这一特殊情况上,并且进行了数值验证。
的)所有根之间在算术性质上的联系,我在那一天(起床前)成功地看清了这个关系,所以我得以当场把它应用到十七边形这一特殊情况上,并且进行了数值验证。
高斯定理的完整证明不在本书论及的范围内,但我们可以介绍他的大体思路。我们首先展示他的论述在正五边形的情况中如何展开,然后简略叙述十七边形和更一般的正多边形的情况。
我们把五边形的顶点看作五个五次单位根,也就是  的五个根。其中一个根是
的五个根。其中一个根是  ,所以多项式可以被分解为
,所以多项式可以被分解为  。因此我们只需要关注
。因此我们只需要关注  的四个根。如图 19.3 所示,它们是两对共轭复数:
的四个根。如图 19.3 所示,它们是两对共轭复数: 和
和  、
、 和
和  。
。
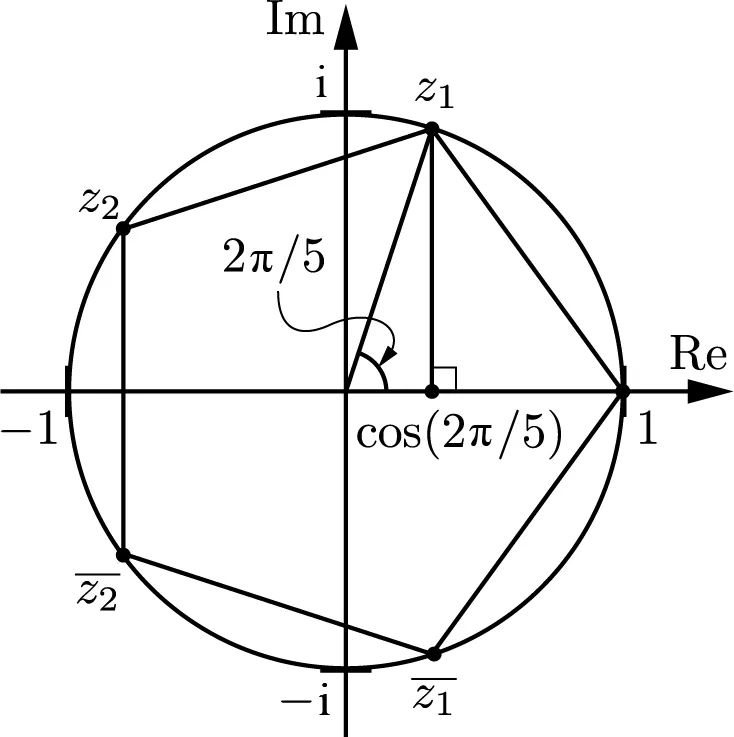
图 19.3 复平面的一个正五边形
这两对共轭复数有两个友好的性质。首先,和其他共轭复数一样,当我们把它们加起来时,虚部会抵消,实部会变成两倍。所以  。其次,它们都在单位圆上,所以互为倒数 :
。其次,它们都在单位圆上,所以互为倒数 : 。应用这两个性质,我们发现
。应用这两个性质,我们发现

我们想求满足  的
的  值。但因为知道
值。但因为知道  ,所以我们可以把方程两边同时除以
,所以我们可以把方程两边同时除以  ,这样可以得到
,这样可以得到

其中  。根据二次方程求根公式,
。根据二次方程求根公式, 。
。
到这里就可以停下了;我们已经获得了足够多的信息,足以用尺规作出正五边形。这两个实数是五边形剩余四个顶点的实部的两倍。所以  。正如在第 1 章所描述过的,我们可以在复平面作出点
。正如在第 1 章所描述过的,我们可以在复平面作出点  ——或者说笛卡儿平面中的点
——或者说笛卡儿平面中的点  ——然后过这一点作实轴的垂线。垂线和单位圆交于
——然后过这一点作实轴的垂线。垂线和单位圆交于  和
和  。然后我们就可以用圆规找出剩余的顶点。
。然后我们就可以用圆规找出剩余的顶点。
不过,我们还是不要这样做。让我们继续行至终点,求出所有顶点的坐标。因为  ,我们可以通过解二次方程
,我们可以通过解二次方程  来求出
来求出  。其中,
。其中, 的值就是上面求得的两个根
的值就是上面求得的两个根  。点
。点  和
和  是二次方程
是二次方程  的根。由求根公式可知,它们是
的根。由求根公式可知,它们是  。所以这两个点的坐标是
。所以这两个点的坐标是  。用类似的步骤可以得到另两个顶点:
。用类似的步骤可以得到另两个顶点: 。
。
这些复杂的计算中可供我们借鉴的地方在于,要求四次方程的根,我们可以把问题简化为求三个二次方程的根,其中一个根的系数是整数,而另两个根的系数包含第一个的根。最后,这些顶点的坐标包含有理数的双重平方根。
高斯对于十七边形的分析与此类似,但需要解更多的二次方程。这些二次方程的根可能包含更多双重平方根。我们简略介绍一下其中涉及的数学。
如图 19.4 所示,假设  是正十七边形的顶点。高斯证明了一个有关质数的定理,该定理让他能够用一种特殊的顺序排列顶点(
是正十七边形的顶点。高斯证明了一个有关质数的定理,该定理让他能够用一种特殊的顺序排列顶点( 除外):
除外): 。他证明,隔项求和得到的两个复数
。他证明,隔项求和得到的两个复数

是二次方程  的根。因此,
的根。因此, 和
和  可以用平方根表示;具体来说,
可以用平方根表示;具体来说, ,
, 。接下来,求
。接下来,求  的隔项和,得到复数
的隔项和,得到复数  以及
以及  。求
。求  的隔项和来得到
的隔项和来得到  和
和  。这两组复数分别是二次方程
。这两组复数分别是二次方程  和
和  的根。所以它们也可以用双重平方根来表示,比如,
的根。所以它们也可以用双重平方根来表示,比如, ,
, 。最后,用类似方法定义
。最后,用类似方法定义  、
、 ,直到
,直到  。这些值是以整数以及
。这些值是以整数以及  、
、 、
、 、
、 为系数的二次方程的根。例如,
为系数的二次方程的根。例如, 和
和  是方程
是方程  的根。因此,这些根也可以写成多重平方根的形式。以
的根。因此,这些根也可以写成多重平方根的形式。以  为例,我们有
为例,我们有  。最后,我们能发现
。最后,我们能发现  是
是  的共轭复数,因此
的共轭复数,因此  。如果我们把
。如果我们把  和
和  代入
代入  和
和  ,再把这两个值代入
,再把这两个值代入  ,然后化简,就能得到高斯推出的表达式
,然后化简,就能得到高斯推出的表达式

而这个数是可作图数!
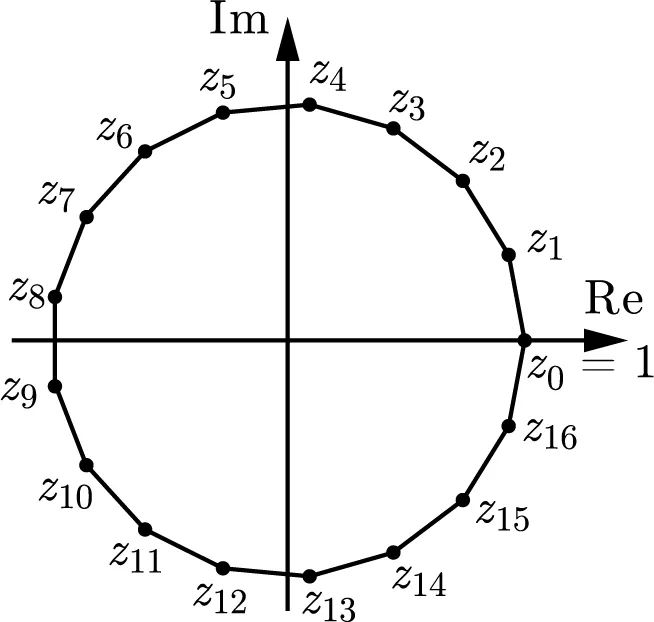
图 19.4 复平面的一个正十七边形
这大体上就是高斯使用的方法。他想要求  的根,其中
的根,其中  是质数。因为
是质数。因为  是这个多项式的一个根,我们只需要求
是这个多项式的一个根,我们只需要求  的根。
的根。 是质数,但
是质数,但  则不一定是质数。假设
则不一定是质数。假设  可以被质因数分解为
可以被质因数分解为  。高斯把这个问题化简为依次求次数为
。高斯把这个问题化简为依次求次数为  的多项式的根。第一个多项式的系数是整数。后续多项式的系数由前面已经解出的多项式的根决定。
的多项式的根。第一个多项式的系数是整数。后续多项式的系数由前面已经解出的多项式的根决定。
高斯发现,如果  是 2 的幂,那么
是 2 的幂,那么  。所以我们就能通过解一系列二次方程来求得
。所以我们就能通过解一系列二次方程来求得  的根。因此这些根都是可作图的。简而言之,如果
的根。因此这些根都是可作图的。简而言之,如果  是质数,正
是质数,正  边形就是可作图的。
边形就是可作图的。
这个  值仍然不是费马质数的形式。但是,如果
值仍然不是费马质数的形式。但是,如果  是质数,那么指数
是质数,那么指数  一定是 2 的幂。
一定是 2 的幂。
假设  不是 2 的幂,那它就有一个奇因数
不是 2 的幂,那它就有一个奇因数  。于是我们就有
。于是我们就有  (有可能
(有可能  )。这样的话,
)。这样的话,

也就是说, 不是质数。
不是质数。
最后,假设  ,其中
,其中  且
且  为不同费马质数。我们可以先作出正
为不同费马质数。我们可以先作出正  边形,然后使用基于等边三角形和正五边形作正十五边形的技巧,作出正
边形,然后使用基于等边三角形和正五边形作正十五边形的技巧,作出正  边形。最后,再加倍边数
边形。最后,再加倍边数  次,就可以得到正
次,就可以得到正  边形。这样就证明了高斯定理。
边形。这样就证明了高斯定理。
闲话 镜子
魔镜,魔镜,告诉我,谁是这世上最美的女人?
——格林兄弟,《白雪公主》
米拉镜由乔治·斯克罗吉和 N. J. 吉莱斯皮发明。它是一种帮助学生们学习反射和对称线的教学工具。它由一块有色的亚克力玻璃,以及保持玻璃直立的支架构成。米拉镜的关键特性在于,它既是透明的,又是反光的。所以它既是一面窗,又是一面镜。
要求点  关于直线
关于直线  的反射,我们把米拉镜沿
的反射,我们把米拉镜沿  放置,然后在玻璃的另一端标记出与点
放置,然后在玻璃的另一端标记出与点  的镜像重合的点(图 T.31)。要求点
的镜像重合的点(图 T.31)。要求点  和另一点
和另一点  之间的反射轴,我们把米拉镜放到使得
之间的反射轴,我们把米拉镜放到使得  的镜像与
的镜像与  重合的位置,然后沿着玻璃即可描绘出反射轴。假设经过一个点存在能把另一点反射到已知直线上的直线,我们可以用米拉镜找到这条直线。图 T.32 展示了第四种用途:已知点
重合的位置,然后沿着玻璃即可描绘出反射轴。假设经过一个点存在能把另一点反射到已知直线上的直线,我们可以用米拉镜找到这条直线。图 T.32 展示了第四种用途:已知点  、
、 和直线
和直线  、
、 ,我们可以摆放米拉镜,使得
,我们可以摆放米拉镜,使得  和
和  的反射分别落在
的反射分别落在  和
和  上。
上。
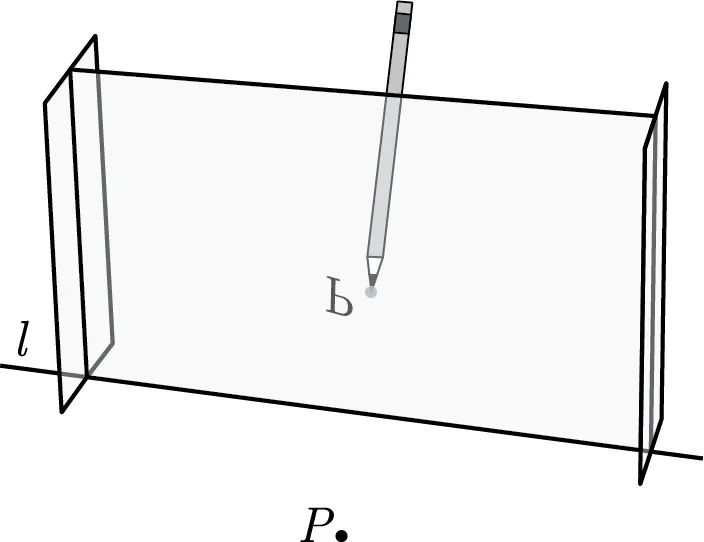
图 T.31 米拉镜关于直线  反射点
反射点 
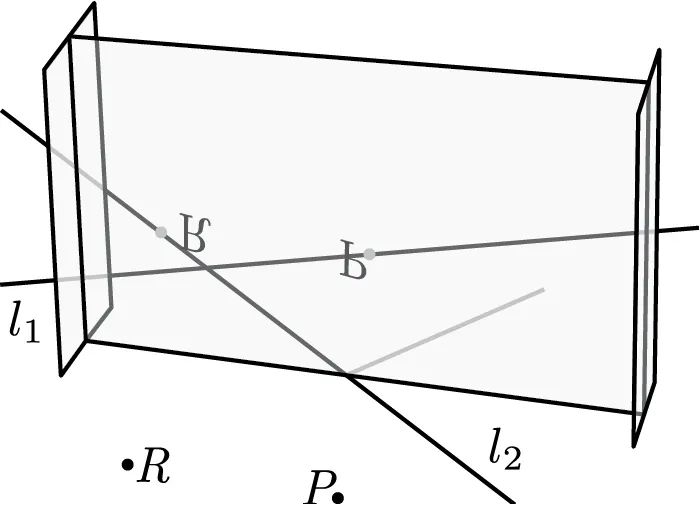
图 T.32 米拉镜把点  和
和  分别反射到
分别反射到  和
和  上
上
令人惊讶的是,这四种操作十分有用。我们不妨想象放弃尺规,仅用米拉镜完成几何作图。虽然不能画圆,但仅使用前三种操作,我们就能作出所有尺规可作图的点。相反,前三种操作也可以用尺规来完成。因此,用前三种操作可以作图的点就是尺规可作图的点。而第四种操作使我们可以作出尺规无法作图的点。我们来看看原因。
抛物线是到直线(准线)和直线外一点(焦点)距离相等的点的集合。如图 T.33 所示,点  到焦点
到焦点  和准线
和准线  的距离相等。事实上,抛物线在
的距离相等。事实上,抛物线在  点的切线
点的切线  平分
平分  。
。 是
是  关于
关于  的反射。换言之,如果我们把米拉镜放在
的反射。换言之,如果我们把米拉镜放在  上,它会把
上,它会把  反射到
反射到  。相反,如果我们把米拉镜放在使
。相反,如果我们把米拉镜放在使  的反射落在
的反射落在  的位置上,那么米拉镜就与抛物线相切。
的位置上,那么米拉镜就与抛物线相切。
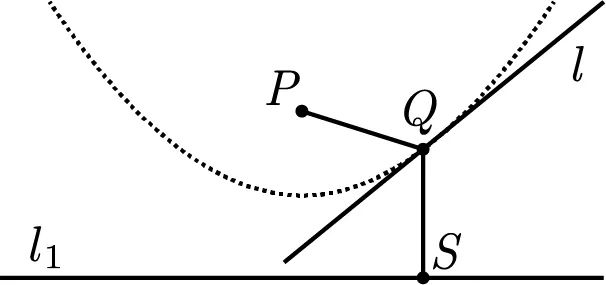
图 T.33 如果我们把点  反射到
反射到  上,那么米拉镜就与焦点为
上,那么米拉镜就与焦点为  、准线为
、准线为  的抛物线相切
的抛物线相切
米拉镜的第四种操作要求我们把两个点反射到两条线上。这一过程相当于找一条与两条抛物线(一条抛物线焦点为  、准线为
、准线为  ,另一条抛物线焦点为
,另一条抛物线焦点为  、准线为
、准线为  )相切的直线
)相切的直线  。正是这些隐藏的抛物线让我们脱离了尺规作图的范畴,并得以解决三等分任意角、倍立方、作正七边形或正九边形以及更多问题。
。正是这些隐藏的抛物线让我们脱离了尺规作图的范畴,并得以解决三等分任意角、倍立方、作正七边形或正九边形以及更多问题。
在米拉镜被发明之前的 1963 年,A. E. 霍克斯坦发明了一种带有镜子的仪器。用这种仪器配合尺规就可三等分角。该仪器由一把长度为  的普通直尺被安装到一片半透明玻璃上制作而成。玻璃与直尺垂直,而且其反射面刚好平分直尺(图 T.34)。
的普通直尺被安装到一片半透明玻璃上制作而成。玻璃与直尺垂直,而且其反射面刚好平分直尺(图 T.34)。
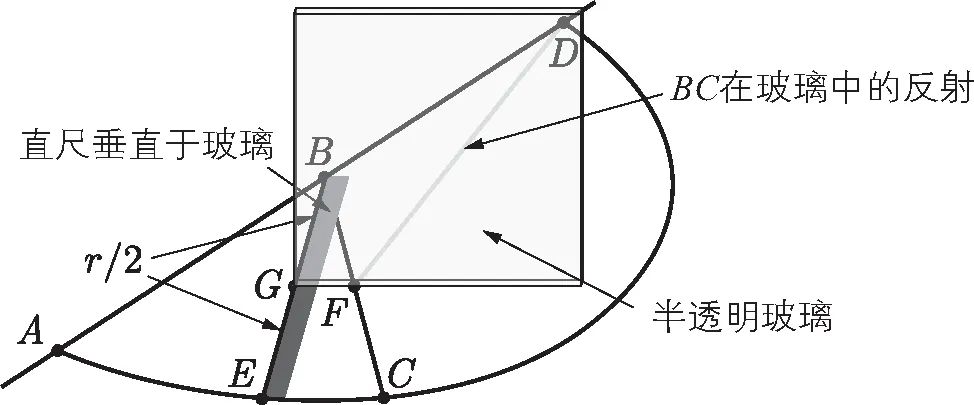
图 T.34 我们可以用一个装有直尺的半透明玻璃三等分角
该工具的用法如下。假设我们想三等分  。简单起见,假设
。简单起见,假设  。用直尺延长
。用直尺延长  ,用圆规以
,用圆规以  为圆心、以
为圆心、以  为半径作圆,交
为半径作圆,交  于
于  。接下来让直尺的一个角与
。接下来让直尺的一个角与  重合,让另一端的角落在圆上。我们可以在玻璃中看到
重合,让另一端的角落在圆上。我们可以在玻璃中看到  的反射。调整直尺的位置,直到该反射经过
的反射。调整直尺的位置,直到该反射经过  。然后我们沿直尺画出
。然后我们沿直尺画出  ,则
,则  三等分角
三等分角  。
。
我们来证明这一结果。首先我们注意到,因为  ,三角形
,三角形  和
和  全等,所以
全等,所以  是等腰三角形(图 T.35)。此外,因为
是等腰三角形(图 T.35)。此外,因为  ,所以三角形
,所以三角形  也是等腰三角形,并且和
也是等腰三角形,并且和  相似。因此
相似。因此  。我们把这三个角记作
。我们把这三个角记作  。因为
。因为  是三角形
是三角形  的外角,所以我们有
的外角,所以我们有  。因此
。因此  。
。

图 T.35 线段  三等分
三等分 
01

《不可能的几何挑战:数学求索两千年》
作者:大卫•S. 里奇森
译者:姜喆
数学历史新角度,作者旁征博引,发掘了之前数学书未曾留意的历史细节。
本书以数学史上四大著名的“古典问题”——化圆为方、倍立方、作正多边形、三等分角为基础,展现了两千多年来,数学家们为解决这些问题而留下的令人拍案叫绝的思想与成就。
02

《微积分溯源:伟大思想的历程》
作者:戴维·M. 布雷苏
译者:陈见柯 林开亮 叶卢庆
从古希腊、古埃及、古印度、中国和欧洲等地的微积分思想,到牛顿、莱布尼茨、伯努利兄弟、黎曼等伟大数学家的辉煌成就,看一看微积分这座“数学宝藏”是如何被塑造成今天的模样的。
03

《贝叶斯的博弈:数学、思维与人工智能》
作者:黄黎原
译者:方弦
法国数学类科普书、大学数学参考及教材类图书畅销书目,在机器学习、人工智能、逻辑学和哲学等众多领域中,探索贝叶斯定理蕴藏的智慧与哲理。
贝叶斯定理一旦与算法相结合,就不再是一套枯燥的数学理论或认识论,而变成了应用广泛的知识宝库,催生了众多现代数学定理,以及令人称道的实践成果。
04

《数学的雨伞下》
作者:[法] 米卡埃尔•洛奈(Mickaël Launay)
译者:欧瑜
惊讶!是思考的起点;
数学,是理解世界本质与万物关联的工具!
以数学为起点,以思考为快乐!
法国数学学会“达朗贝尔奖”得主科普名作。
数学,是理解世界本质与万物关联的工具,它能制造两个指南针:一个叫“实用”,一个叫“优雅”。不懂得数学的意义,就无法真正学习和理解数学。
科学家为什么那么聪明?因为他们有非凡的思考方法。
以数学为工具,以思考为快乐;培养自己的思考力、观察力,成为真正的思考者。
























 5
5

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








