振动分析领域：加速度传感器的量程估算

1.背景知识

振动的国标和国际标准中仅仅可以查阅位移和速度的峰值，不会出现加速度指标。为什么呢？因为一些高频的振动往往体现为一种冲击性的信号，此时作用时间不定，这个指标很难给出。但是并不是不可能。下面常识根据现有资讯来推导相关的加速度阈值选项的参考值：

1.轴承振动

1.1 西交大数据集的参考（超限老化实验）：

数据集关键字：XJTU-SY 轴承 数据集

轴承的加速度峰值已经超过达到30G~50G的水准。为什么会这样吗？

因为轴承四大可能损伤中，外圈内圈故障往往是点蚀，这种振动的作用时间往往很短，同样的力，作用时间越短，加速度越大。记得这个指标，这个轴承只有4cm，转速35转。加速度随转频的提升是线性的，在真实的环境中，轴承的转速往往只有17转以内，轴承故障，加速度与转速一般成正比，所以考虑侦测轴承故障，20G的加速度选择是可以的。

1.2 加速度四个阶段频率轴承故障诊断方法（CN 104833510）

现场实际使用时，轴承终末期阶段，加速度在3个G，此时的频点在500Hz左右。对照西交大的转频，是对应频率的1/4甚至更低。加速度理论上也应当缩减至原有的1/4。

其他配图参见附图，防止原始链接丢失。

如果以实际可能最高频率

按照上图中的信息，把振动传感器的量程设置在20g是比较合适的。 

注意：轴承振动早期， 如果没有引起轴振动，振动限制在轴承本身，它能引发的振动是很微弱的。接下来我们对照标准来计算如果振动由轴法向振动引发，可能的烈度有多大。

2.机械体振动

机械体振动，在ISO 2372中分为三级，这个指标针对国内的技术水平可能偏高：

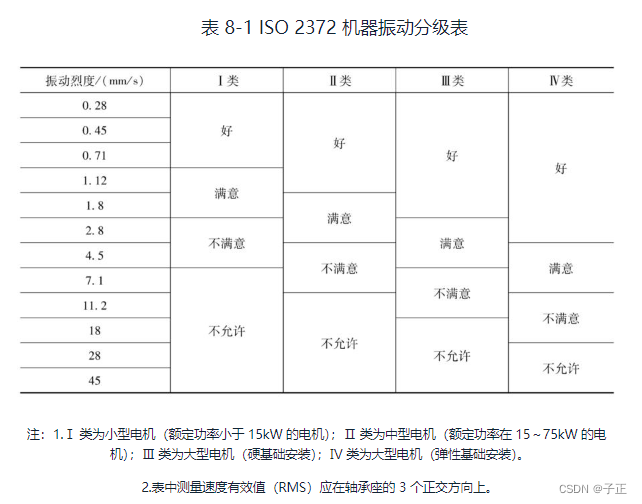
我们以75kW以上级电机的速度烈度门限值为例来说明：

弹性基础安装时的振动门限值为28mm/s

假定，这个振动由不平衡，不对中这类比较缓和的因素产生，假定当前振动转速是国产电机的最高转速3000rpm：

1. 此时加速度相对匀速转动速度函数同为sin函数的形式，则如果幅度为1，时间持续1秒，则最高加速度会在0点出现，其值为1m/s^2
2. 现在按照转速把时间轴压缩到1000rpm(中国制式供电50Hz，三级对儿),则相应加速度值提升到16.67倍。
3. 此时如果峰值有1m/s，修正为28mm/s，则加速度缩减至28/(1*1000)
4. 所以，综合的加速度为：28*16.67/1000 = 0.467 = 46.7e-3 g

转频降低，这个加速度的指标会更低。但是注意，振动往往体现为冲击性的特征，此时，加速度会因为作用力的持续时间更短，几乎会高出几个数量级。

2.1 可以查询到的机械体振动加速度标准：

根据不同的行业和设备类型，振动加速度的标准也有所不同。以下是一些常见的标准：

1.电力设备：根据《电力设备维修技术规程》规定，一般情况下，振动加速度不应超过 2 g。

2.机床设备：根据国际标准 ISO 2372-1084，机床的振动加速度应小于 4.5 g。若超过此范围，则需要进行调整和维修。

3.风机设备：根据《风电机组技术要求规范》规定，风机设备的振动加速度应小于 1.5 g。

4.轴承设备：根据国际标准 ISO 10816-1-1995，轴承设备的振动加速度应不超过 2 g。

注意，这里的指标是刚刚偏离正常工作状态，需要检修的情况，实际上振动的烈度会更大。

2.2 理论计算

轴向振动有不对中和不平衡两种，相应的谱线出现在1倍频和2倍频位置，均为近似正弦波。我们首先推导加速度与速度的换算关系，参考如下数学模型：

2.2.1 加速度与速度换算公式

import numpy as np
import matplotlib.pyplot as plt

# 参数设置
A = 1.0            # 加速度信号的振幅
f = 1.0            # 信号频率 (Hz)*10000/7812
omega = 2 * np.pi * f  # 角频率
T = 1 / f          # 信号周期
Fs = 100           # 采样频率
dt = 1 / Fs        # 采样间隔
t = np.arange(0, T, dt)  # 时间向量

# 生成加速度信号 (正弦波)
acceleration = A * np.sin(omega * t)

# 对加速度信号进行积分，得到速度信号
velocity = np.cumsum(acceleration) * dt  # 使用累积和近似积分
velocity -= np.mean(velocity)  # 去除积分常数（以便速度从零开始）

# 绘制加速度和速度曲线
plt.figure(figsize=(12, 6))

# 加速度曲线
plt.subplot(2, 1, 1)
plt.plot(t, acceleration, label=f'Acceleration  pk {A:.3g}m/s² == {A/9.8:.3g}g')
plt.title(f'Acceleration Signal, {Fs}sa/s {f}Hz')
plt.xlabel('Time [s]')
plt.ylabel(f'Acceleration[m/s²]')
plt.grid(True)
plt.legend()

# 速度曲线
plt.subplot(2, 1, 2)
plt.plot(t, velocity, label=f'Velocity  pk {max(velocity):.3g}m/s == {max(velocity)*1000:.3g}mm/s', color='orange')
plt.title(f'Velocity Signal')
plt.xlabel('Time [s]')
plt.ylabel(f'Velocity [m/s]')
plt.grid(True)
plt.legend()

plt.tight_layout()
plt.show()

通过变换加速度信号频率，幅度，我们能得到如下基本结果： 

2.2.2 加速度速度转换的基本换算关系

1. 振幅为pk =0.1g的1Hz正弦信号，积分后的速度峰值为： 159mm/s
2. 其他参数不变，频率增大10倍：积分后的速度峰值减小10倍
3. 其他参数不变，振幅增加10倍，积分后的速度峰值增大10倍

2.2.3 得到加速度

由速度反推，首先已知：pk=0.1g时，1Hz信号的转频，峰值速度为159mm/s

对于三极对电机，1000转左右，0.1g的加速度会对应0.159 mm/s的速度。

电机加速度换算比：1g == 0.53mm/s*极对数，

2.2.4 理论推导结论：

由2.1节机械振动标准核查：

轴不平衡引发的最大烈度的速度值最高在28左右，所以，对应的加速度量程：

单极对电机的极限加速度量程 = 28/0.53 = 52g，近似50g

3.信噪比和动态范围

在振动分析中，往往要在异常出现早期，即具有故障分析能力，此时，振动的特征谱线，往往是依赖于特定原始谱线，或者基于原始工作状态的一个比例值,

原始摘引：值得收藏的机械设备振动标准，太实用了（2） - 知乎

动态范围以为着要在振动的峰值范围内提供100倍的AD精度。注意往往在这个阶段，振动还没有恶化到上述阈值范围，所以，振动传感器的量化范围，至少要求9,10位甚至更靠上。

4 结论(<=20g,9Bits)

按最高功率电机，最高振动烈度解算，加速度的极限量程在50g左右。

建议的适应传统工业振动监测的传感器，推荐的加速度量程：

对于75KW以上级电机是：不高于20g.（按转频1000Hz计算）

15KW电机，转频不变，仍然不可低于20g.

考虑动态范围至少选择9位AD以上的。

附录A 一组振动阈值摘要：

这种震动的测量值区间：

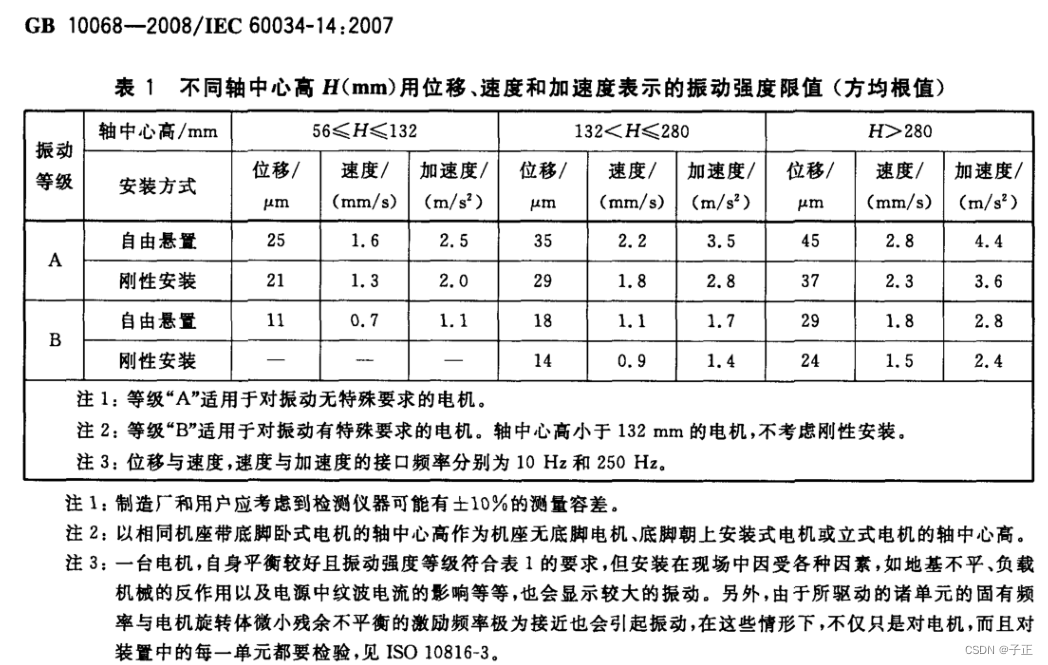
GB10068-2008的加速度值仅针对电机，它的振动水平影响了整个机械组合体的振动水平，所以这个允许的振动范围是比较小的：

不过，如果位移是45um，这个位移可能指PkPk，那么速度 = 45e-6/(1/50*3/2) = 1.5 mm/s 奇怪，这里与GB10068-2008差1倍。加速度 = 1.5e-3/s(1/50*3/4) = 0.1m/S^2,  这个值与GB10068-2008差40倍。不知道为什么。可能它考虑了振动的基本特征是冲击响应的形式。

附录B：实际使用环境，轴承振动的渐进式恶化过程

原始知乎的摘引

1） 加速度频谱频程在 3333—5000Hz 为早期贪油阶段

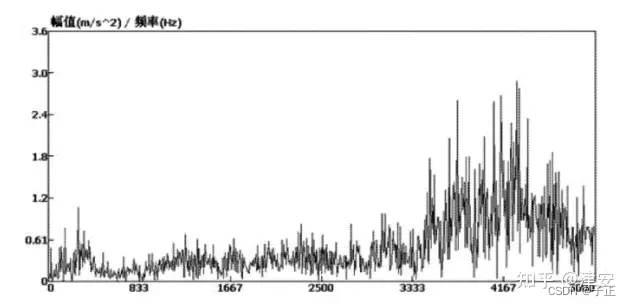
附录C 加速度 - 速度积分数学模型输出值：

C.1 其他参数不变，转速增大10倍，速度降低10倍。成反比。

C.2 其他参数不变，加速度增大10倍，速度增加10倍。成正比。 

附录D 电机书输出轴切向力大小计算公式：

import math

def calculate_axial_force(power_kw, speed_rpm, shaft_diameter_mm):
    # 假设额定功率、额定转速和轴径
    # 电机功率 (功率需要转换为瓦特)
    power_watt = power_kw * 1000

    # 轴转速 (转速可以直接使用)
    speed_rpm = speed_rpm

    # 轴径 (以米为单位)
    shaft_diameter_m = shaft_diameter_mm / 1000

    # 示例计算，实际计算需要考虑更多因素
    # 假设轴向力与功率和转速有关的一个简单模型
    # 这只是一个假设示例，具体计算需参考实际工程设计规范
    axial_force_newton = power_watt / ((speed_rpm/60) * (shaft_diameter_m*3.14))

    return axial_force_newton

# 电机参数
power_kw = 15
speed_rpm = 970
shaft_diameter_mm = 48

# 计算轴向力
axial_force = calculate_axial_force(power_kw, speed_rpm, shaft_diameter_mm)
print(f"计算得到的轴向力为: {axial_force:.2f} 牛顿")

附录 E 一个失败的加速度速度推算

合适的推理过程参见：2.3.3

对于电机而言，15KW,17KW 3极对儿电机的典型输出扭矩换算到电机输出轴的切向力大小分别为：

• 15kW...........970转.......轴径48mm..........最大扭矩可以达到额定扭矩2.1倍。
• 75kW...........985转.......65mm..................最大扭矩2.0倍；

15kW的额定切向力为：Fq = 15*e3/((970/60*.3.14) *1000/48) =  6156牛

75KW的额定切向力为：Fq = 75*e3/((985/60*.3.14) *1000/48) =  22383.77牛 

现场使用时的极限工况会加倍。

那么在输出轴上如果出现问题，可能的最大加速度为
F = ma,根据反作用原理，这个力会作用到到轴+转子这个部件上。

《终止》