LLC电路 - 变压器匝比改变时的连锁反应

1.谐振电路等效电阻Rac

等效电阻从负载一侧映射过来，假定负载电阻为R，功率计算公式为U_out^2/R，则理想变压器因为Uin = N*Uout，所以等效电阻的阻值变化是平方关系：Rref = K*R*N^2.具体的计算公式为：

Vp为变压器初级线圈两侧电压。

2.变压器匝数比改变下的连锁反应

如果n已经在下降，假定因为压控负反馈环路，需要让最终Vo稳定。那么，Vp也必须要抬升。

如果减小n，负载电阻不变，Rac在以n^2的关系在快速下降。此时正常情况，Vp已经在线性下降，如果此时需要稳定Vp，初级线圈的电流需要线性上升才行。也就是此时线圈此时起码需要线性上升。

然后，因为Rac还参与前级谐振电路的品质因数计算：

Rac，随N的减小，平方反比增加，假定谐振电路的谐振电容电感参数不变，品质因数提升。此时谐振电路在负载电阻Rac处的增益在增大。

对LLC谐振电路而言，谐振电路的增益最高只能为1。因为他没有额外的放大电路，纯粹是分压。

分压值在谐振状态，LC抵消，所以分压近乎完全加载在变压器初级线圈，此时增益接近1.

增益计算公式：

也就是各种Q值所描述的LC谐振电路的Q值图，Q值虽然在变化，但是系统的整体增益，都是在谐振频率顶点处达到近似0db——1：1

为了让电流只是线性提高，谐振电路的实际工作频点，似乎条件不足，无法分析。

3.小结：

如果变压器匝比变小,相同负载：

1.变压器初级线圈电流会增大。
2.谐振电路的品质因数会提升。

4.变压器谐振电路与开关电路的适配 

因为初级线圈在一个工作循环内，处于三角波充放电状态。然后，这个等效电流

Im = Vpp/4.

然后对电感：V = Ldi/dt， 如果是三角波的横流充电模式，di/dt的斜率 = V/L

所以有上面的Im公式。Ip是开关电路，实际流入谐振网络的电流。剩余的部分，会被前级的开关电路，因为死区时间吃掉。

Ip必须要大于的那个部分，相当于在一个工作循环内，MOS管各种寄生电容充放电累积的能量。

此时，开关管电路的电压不变：

V=I*dt/C
所以：I = Vin*C/dt.

4.1 这部分能量是什么？

我们首先计算电感一侧，初级线圈视角的能量：

示例文档中：

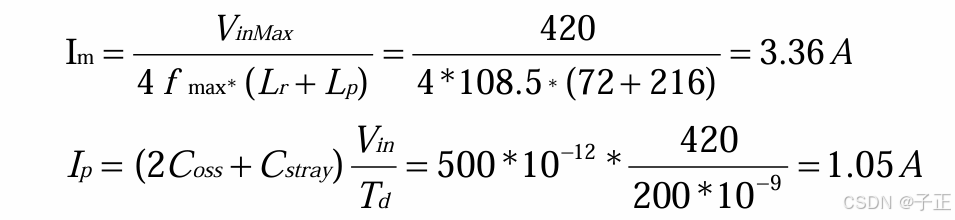
首先Lp变压器分压值 = 420*216/(72+216) = 420*0.75 = 315V
然后电流直接是有效值，所以，这部分能量有：P = 315*3.36 = 1kW
示例器件的设计目标输出功率只有：

所以这部分功率就是用来实际做功的。

所以看起来谐振电路的工作原理是在主变压器和其它容性器件，平衡的震荡过程中，泼出去了一些能量。震荡的能量本身已经很高了。甚至比实际要输出的能量还要高。

5.电路模拟和增益曲线绘制

5.1 电路模拟

电路模拟可以使用免费的LTSpice，电路的核心部分只是LLC振荡回路，所以，可以直接手搭：

集成的示波器可以直接查看各处的输出波形。

5.2 系统增益曲线绘制

增益曲线可以看到整个系统的Vin/Vout的增益情况：

注意上图中增益=1的部分，对应的就是谐振频率。谐振频率处并不是LLC系统整体增益的最高点。这一点稍后再分析。然后上面的图形核心的代码片段：

import numpy as np
import matplotlib.pyplot as plt

# 电路参数
#V_in = xx  # 输入电压，单位：V
#L_r = xxe-6  # 电感，单位：H
#C_r = xxe-9*8  # 电容，单位：F
#L_m = xx*L_r
#f0 = 1/(2*np.pi*np.sqrt(L_r*C_r))  # 谐振频率，单位：Hz
#R_ac = xx  # 变压器的等效电阻，单位：Ω

# 频率范围
frequencies = np.linspace(10e3, 150e3, 1000)  # 从10kHz到100kHz

# 计算增益
gains = []
for f in frequencies:
    omega = 2 * np.pi * f
    
    # 计算等效阻抗
    Z_Lm = 1j * omega * L_m
    Z_Lr = 1j * omega * L_r
    Z_C = -1j / (omega * C_r)
    
    Z_parallel = (Z_Lm * R_ac) / (Z_Lm + R_ac)
    Z_eq = (Z_Lr + Z_C) + Z_parallel
    
    # 计算增益
    V_out = V_in * np.abs(Z_parallel) / np.abs(Z_eq)
    gain = V_out / V_in
    gains.append(gain)

# 转换为numpy数组
gains = np.array(gains)

# 绘制增益曲线
plt.figure(figsize=(10, 6))
plt.plot(frequencies / 1e3, gains, label=f'R_ac = {R_ac} Ω Freq_r={f0/1e3:.2f}kHz')
plt.xlabel('Frequency (kHz)')
plt.ylabel('Gain')
plt.title('LLC Resonant Circuit Gain vs Frequency')
plt.grid(True)
plt.legend()
plt.show()

附录A 变压器匝比减小时-为了维持次级电压和驱动能力优先提升初级线圈电流还是提升工作频率

》》假定一个变压器的匝数比变小，这个变压器的次级电压必须稳定，可调整的参数是前级的输入电流和频率。这个时候，电流和频率优先提升哪一个，最终的变压器的温升会更小？

在变压器匝数比变小的情况下，如果需要保持次级电压稳定，可以通过调整前级的输入电流和频率来实现。为了使变压器的温升更小，优先考虑提升频率而不是电流。

这是因为提升频率可以增加变压器的效率，减少铁损，同时在一定范围内不会显著增加铜损。而增加电流会直接增加铜损，导致变压器发热增加，从而使温升加大。

具体原因如下：

频率的影响：提高频率会使磁通密度变化更快，从而在一定程度上减少所需的磁通量，这有助于降低铁损（磁滞损耗和涡流损耗）。因此，提高频率通常可以提高变压器的效率，减少发热。

电流的影响：增加电流会直接增加铜损（I²R损耗），因为铜损与电流的平方成正比。这会直接导致变压器发热增加，从而使温升加大。

因此，在需要保持次级电压稳定且希望变压器的温升更小的情况下，优先提升频率会是一个更优的选择。当然，频率的提升也有其限制，比如需要考虑铁芯材料的频率响应和绕组的设计等因素，以避免高频下的其他损耗增加。

总结：优先提升频率，以减少变压器的温升。

内容由AI生成，无法确保真实准确，仅供参考

》》但是铁损的涡流损耗在频率提高时不是也是在以平方水平在提升吗？

您说得对，提高频率确实会导致铁损中的涡流损耗增加，因为涡流损耗与频率的平方成正比。然而，在实际应用中，选择频率和电流的优化组合取决于变压器的设计和其他操作条件。

在这种情况下，考虑以下几点可能会更清楚：

铜损与铁损的平衡：虽然提高频率会增加涡流损耗，但它也可以减少磁通密度，从而降低磁滞损耗。如果设计得当，总铁损的增加可能不会导致整体的温升大幅上升。而铜损（I²R）的增加是直接且显著的，因此我们需要谨慎地选择频率和电流的最佳组合。

变压器的容量：变压器的额定容量和冷却系统的效率也会影响温升。如果变压器有足够的冷却能力，那么可以承受更高的温升而不影响其寿命。

频率的上限：变压器的设计有一定的频率上限，超过这个上限可能导致绝缘材料的老化和机械振动增加。因此，提高频率应该在允许的范围内进行。

综上所述，虽然提高频率会增加涡流损耗，但在合理的范围内，这可能是一个更好的选择，因为它可以降低磁滞损耗并提高整体效率。同时，应该避免过高的频率以防止其他损耗的增加。

因此，答案可能需要在实际操作中通过测试和调整来确定最佳的频率和电流组合，以实现次级电压的稳定同时最小化变压器的温升。在实际操作中，通常会进行详细的损耗分析和热分析，以找到最优的解决方案。

内容由AI生成，无法确保真实准确，仅供参考

》》变压器如果额定负载工作频点在100kHz附近，这个时候，为了稳住次级电压，增大电流带来的温升更小还是增加频率带来的温升更小？
在变压器额定负载工作频率在100kHz附近时，为了稳住次级电压，我们需要比较增大电流和增加频率带来的温升效果。考虑到您已经提到变压器的工作频点在100kHz附近，这意味着变压器已经处在一个相对高的频率范围内，因此我们需要更细致地分析两种方式的影响。

1. 增大电流带来的温升
增大电流会直接增加变压器的铜损（I²R损耗），因为铜损与电流的平方成正比。这会导致变压器内部的温度升高，特别是绕组部分的温升。由于铜损是直接由电流引起的，因此这种方式的温升是非常直接和显著的。

2. 增加频率带来的温升
增加频率会带来以下几个方面的影响：

涡流损耗：涡流损耗与频率的平方成正比，因此在高频下，涡流损耗可能显著增加。
磁滞损耗：磁滞损耗与频率成正比，虽然相对涡流损耗来说影响较小，但在高频下也不能忽视。
其他高频效应：高频下可能还会出现集肤效应和邻近效应，这些效应会增加导线电阻，从而增加额外的铜损。
然而，增加频率也可以减少磁通密度，从而在一定程度上降低整体铁损。同时，高频工作可能还会带来效率的提升，因为高频变压器通常设计得更紧凑，能量转换效率更高。

比较分析
在100kHz附近工作时，变压器已经处在一个高频状态下。此时，增加频率带来的涡流损耗和磁滞损耗可能会显著增加，但同时也可以通过减少所需的磁通密度来平衡部分铁损。相比之下，增大电流带来的铜损增加是非常直接且显著的。

结论
在这种情况下，为了稳住次级电压同时尽量减少变压器的温升，增加频率可能是更好的选择。尽管增加频率会带来一些额外的损耗，但通过优化设计和材料选择，可以尽量减少这些损耗，同时保持较高的效率。而增大电流则直接且显著地增加铜损，导致温升更为明显。

因此，在变压器额定负载工作频点在100kHz附近时，增加频率带来的温升可能相对较小，但需要在实际操作中进行详细的损耗分析和热分析，以确定最佳的频率和电流组合。