Programming Exercise 4:Neural Networks Learning
这周总结一下Week5的作业,需要实现三层神经网络内部参数的训练。应用的例子同Week3一致,均为识别手写数字。总的来说本周作业较前几次难度略有提升。
数据预处理上与上一周类似,此处不再赘述。
sigmoidGradient.m目的是给出在backpropagation(反向传播)过程中各层的误差分配。
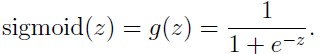
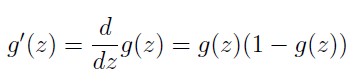
g=sigmoid(z)*(1-sigmoid(z));randInitializeWeights.m目的是对神经网络各层的参数进行初始化,注意这里的参数不能够全部相同,否则会导致训练后参数全部相同,无法达到精度要求。最简单的方法就是在随机产生一个相同维度矩阵的基础上进行适当修改。
epsilon_init = 0.12;
W = rand(L_out, 1 + L_in) * 2 * epsilon_init-epsilon_init;
L_in和L_out是该层网络的输入和输出链接数,由于要加一个常数项,输入链接加1。W中的元素在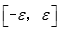
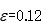
nnCostFunction.m这次误差函数里面可是相当有料啊!包含前向传播和后向传播两块内容。参数矩阵第一层25x401,第二层10x26。
前向传播:
误差函数比较好处理。
y是训练样本的类别向量5000x10,从初值到需要经过2次正向传播,对每层参数实施正则化。
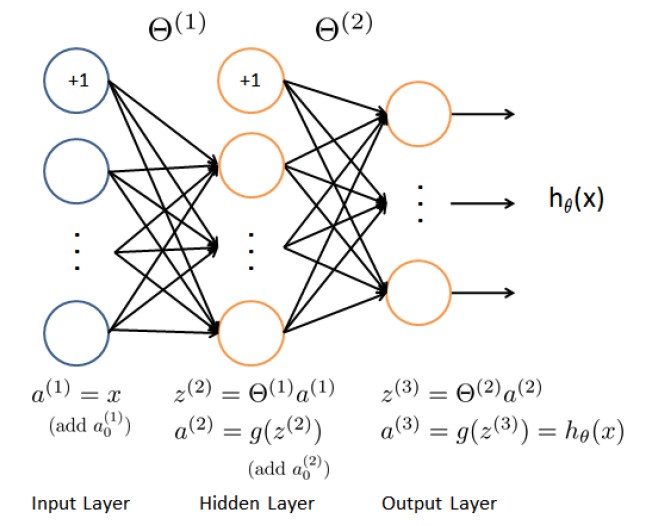
%calculate h(x)
a1 = [ones(m, 1) X];
z2 = a1 * Theta1';
a2 = sigmoid(z2);
a2 = [ones(m, 1) a2];
z3 = a2 * Theta2';
h = sigmoid(z3);
%calculate yk
yk = zeros(m, num_labels);
for i = 1:m
yk(i, y(i)) = 1; %y is class vector
end
%costFunction
J = (1/m)* sum(sum(((-yk) .* log(h) - (1 - yk) .* log(1 - h))));
%Regularized cost function,Theta1 and Theta2 are the weight matrices
Theta1_new=Theta1(:,2:size(Theta1,2));
Theta2_new=Theta2(:,2:size(Theta2,2));
J=J+lambda/2/m*(Theta1_new(:)'*Theta1_new(:)+Theta2_new(:)'*Theta2_new(:));反向传播:目的在于把每次正向传播的误差反馈给每层的参数并按照梯度给出的最优方向进行调整。
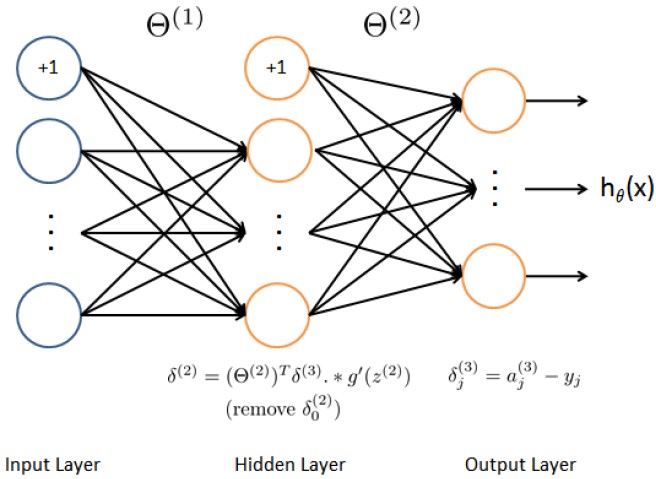
步骤:1.实施正向传播到第三层时,算出与真值的误差。
2.利用sigmoid函数的梯度,算出第二层的误差矩阵。
3.计算各层的梯度(注意要去掉第一列,即常数列)。
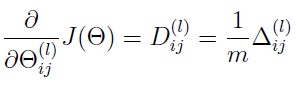
4.正则化。
%step 1 and 2
for i=1:m
y_new=zeros(1,num_labels);
y_new(1,y(i))=1;
a1=[1;X(i,:)'];
a2=[1;sigmoid(Theta1*a1)];
a3=sigmoid(Theta2*a2);
det3=a3-y_new';
det2=Theta2'*det3.*sigmoidGradient([1;Theta1*a1]);
det2 = det2(2:end);
Theta1_grad=Theta1_grad+det2*a1';
Theta2_grad=Theta2_grad+det3*a2';
end
%step 3 and 4
Theta1_grad(:,1)=Theta1_grad(:,1)/m;
Theta1_grad(:,2:size(Theta1_grad,2))=Theta1_grad(:,2:size(Theta1_grad,2))/m+...
lambda*Theta1(:,2:size(Theta1,2))/m;
Theta2_grad(:,1)=Theta2_grad(:,1)/m;
Theta2_grad(:,2:size(Theta2_grad,2))=Theta2_grad(:,2:size(Theta2_grad,2))/m+...
lambda*Theta2(:,2:size(Theta2,2))/m;最终精度为95.06%,这与作业要求相近。
总结一下,反向传播里面梯度和误差矩阵那里还是有一些似懂非懂;程序里面还可以再简化一下,以后再贴上来;本身是数学系的,而且自认为高代学得还可以,还是差点被里面加减项搞晕,还是要再好好琢磨一下里面的原理。












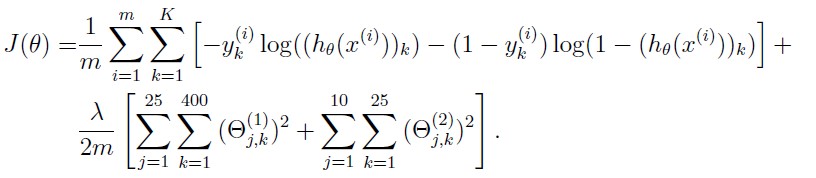
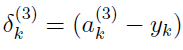
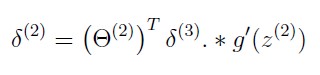

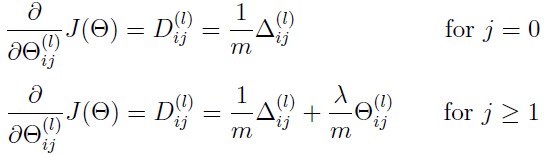














 248
248

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








