Coursera_Stanford_ML_ex5_正则多项式回归和误差分析 作业记录

Programming Exercise5:Regularized Linear Regression and Bias v.s. Variance

       这周总结一下Week6的作业，实现正则化多项式回归，画出训练误差和交叉测试误差随训练用例数量变化的曲线，分析高偏差和高方差的影响因素，最后画出的取值变化对误差的影响曲线。总体上来说难度不大。

       首先看一下作业要求（打星号的需要提交）：

       首先分析一下数据，ex5data1.mat中的X表示水库中水位的变化，y表示水坝放水量；Xval，yval表示交叉测试集中对应的量。

       linearRegCostFunction.m中需要实现误差函数以及梯度函数，和之前线性回归的一致。废话不多说，直接上程序。

<span style="font-family:SimSun;font-size:18px;">J=J+(X*theta-y)'*(X*theta-y)/2/m+lambda*(theta(2:end,1)')*theta(2:end,1)/2/m;
grad(1,1)=1/m*X(:,1)'*(X*theta-y);
grad(2:end,1)=1/m*X(:,2:end)'*(X*theta-y)+lambda/m*theta(2:end,1);</span>

  结果如下：

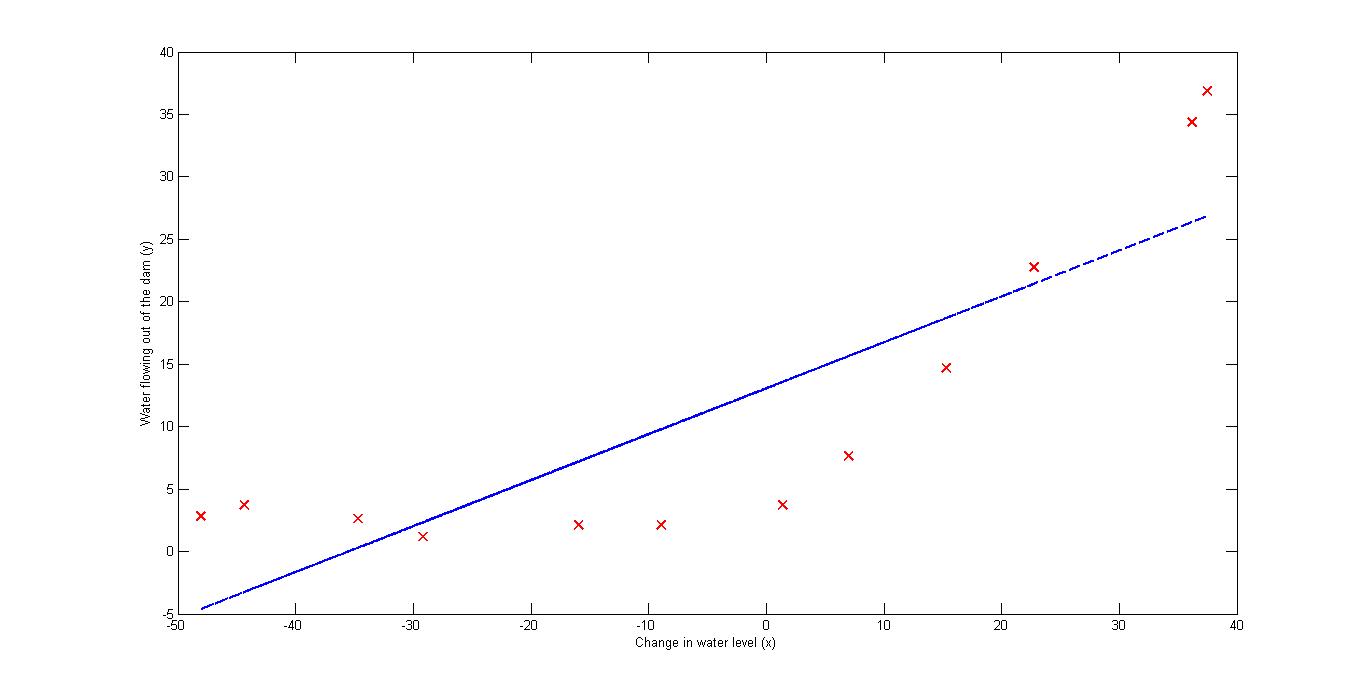
  polyFeatures.m需要将线性回归进行扩展，引入高次项。具体做法是将原本是向量的X扩展成行数不变，列数为多项式最高次的矩阵。

X_poly = zeros(numel(X), p);
for i=1:numel(X)
    for j=1:p
        X_poly(i,j)=X(i).^j;
    end
end

  结果如下：

  learningCurve.m用于得到在训练用例数量变化时的两类误差值。

for i=1:m
    [theta] = trainLinearReg([ones(i, 1) X(1:i,:)], y(1:i,:), lambda);
    error_train(i,1)=linearRegCostFunction([ones(i,1) X(1:i,:)], y(1:i,:), theta,0);
    error_val(i,1)=linearRegCostFunction([ones(size(Xval,1),1) Xval],yval, theta,0);
end

  主要的思想就是每一次加一个训练样本中的例子并重新训练得到参数值，然后算出对应集合的误差。需要注意在error_train只是对用于训练的样本求误差。

  结果如下：1.Learning curve for linearregression

        2. Polynomial Regression Learing Curve

  validationCurve.m用于找出使lambda交叉测试误差达到最小的。

Lambda_vec=[0 0.001 0.003 0.01 0.03 0.1 0.3 1 3 10]’
for j=1:length(lambda_vec)
    lambda=lambda_vec(j);    
    [theta] = trainLinearReg(X, y, lambda);
    error_train(j,1)=linearRegCostFunction(X, y, theta,0);
    error_val(j,1)=linearRegCostFunction(Xval,yval, theta,0);
end

  结果如下：

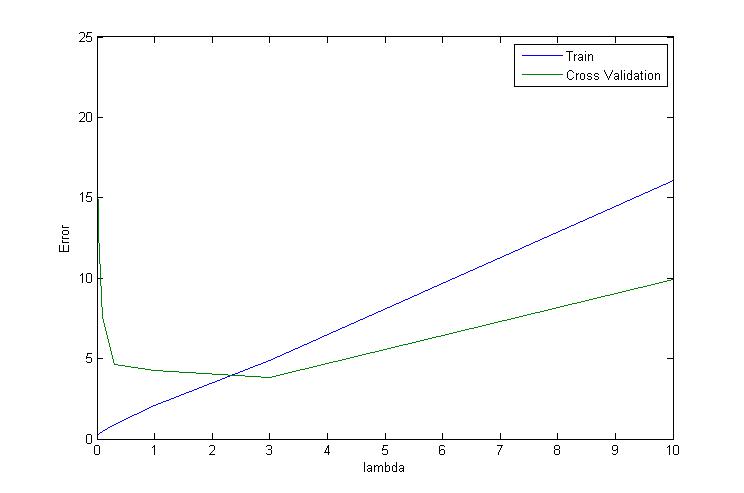
  很明显能够看出在3附近时，使交叉测试误差达到最小。

  总结：学会使用误差分析图来确定模型需要在哪方面进行改进以及如何寻找最优的值是本周的重点。