机器学习笔记 - 贝叶斯学习（5）

贝叶斯置信网

如前两节所讨论的，朴素贝叶斯分类器假定了属性$a_1,a_2...a_n$的值在给定目标值$v$下是条件 独立的。这一假定显著地减小了目标函数学习的计算复杂度。 当此条件成立时，朴素贝叶斯分类器可得到最优贝叶斯分类。

然而在许多情形下，这一条件独立假定明显过于严格了。在大多数情况下，属性之间会有一些联系，例如在（4）中最后例子中的属性$outloock = sunny$和$Wind=Strong$ 一般不会同时出现，这样说明属性之间还是有联系的。

朴素贝叶斯分类器假定所有变量在给定目标变量值时为条件独立的，与此不 同，贝叶斯置信网中可表述应用到变量的一个子集上的条件独立性假定。也就是说贝叶斯置信网选择属性集中的一部分是条件独立，另一部分是有依赖关系的，这样显然更贴近实际。

一般来说，贝叶斯置信网描述了在一组变量上的概率分布。考虑一任意的随机变量集合 $Y_1…Y_n$，其中每个$Y_i$可取的值集合为$V(Y_i)$。定义变量集合Y的联合空间(joint space)为叉乘$V(Y_1 ) × V(Y_2)…V(Y_n)$。换言之，在联合空间中的每一项对应变量元组的一个可能的赋值 <Y1…Yn> <script type="math/tex" id="MathJax-Element-9"> </script>。 在此联合空间上的概率分布称为联合概率分布(joint probability distribution)。联合概率分布指定了元组 <Y1…Yn> <script type="math/tex" id="MathJax-Element-10"> </script>的每个可能的变量约束的概率。贝叶斯置信网则对一组变量描述了联合概率分布。

1. 条件独立性

令 X,Y和 Z 为 3 个离散值随机变量。当 X服从的概率分布独立于给定 Z 值时 Y 的值，称 X在给定 Z 时条件独立于 Y，即：

其中$x_i ∈ V( X) ， y_j ∈ V(Y) ， z_k ∈ V(Z)$。通常将上式简写为$P(X|Y,Z)=P(X|Z)$。

而朴素贝叶斯分类器假定给定目标值V时，实例属性$A_1$条件独立于实例属性$A_2$。这使得朴素贝叶斯分类器可以按照 下式计算式中的$P(A_1 ,A_2 |V)$：

$$P(A_1 ,A_2 |V) = P(A_1|A_2 ,V)P(A_2|V)$$
$$=P(A_1|V)P(A_2|V)$$
第一个用的是乘法法则（ $P(AB)=P(A|B)P(B)=P(B|A)P(A)$），第二个用的是条件独立性的公式。

2. 表示

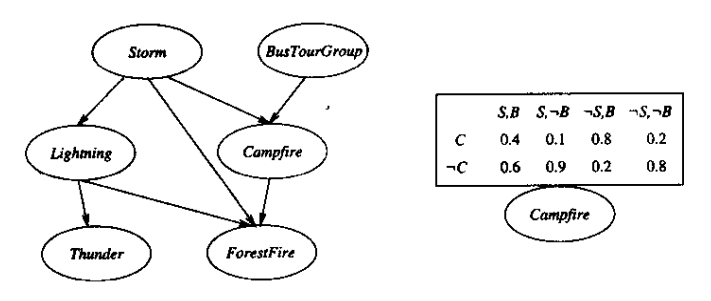
贝叶斯网表示联合概率分布的方法是指定一组条件独立性假定（它表示为一有向无环图），以及一组局部条件概率集合。联合空间中每个变量在贝叶斯网中表示为一结点。对每一变量需要两种类型的信息。
1、网络弧表示断言“此变量在给定其立即前驱时条件独立于其非后继”。 当从Y到X存在一条有向的路径，我们称X是Y的后 继。例如在上图中，Campfire的直接前驱为Storm 和BsuTourGroup， 而后继是Forestfire，Campfire 在给定其父结点 Storm 和 BusTourGroup 时条件独立于其非后继 Lighting 和 Thunder 。
2、对每个变量有一个条件概率表，它描述了该变量在给定其立即前驱时的概率分布。

对网络变量的元组 <Y1…Yn> <script type="math/tex" id="MathJax-Element-19"> </script>赋以所希望的值 $（ y_1 …y_n ）$的联合概率可由下面的公式计算：

$$P(y_1,...,y_n)=\prod_{i=1}^nP(y_i|Parents(Y_i))$$

其中$Parents(Y_i)$表示网络中Yi的立即前驱的集合。注意 $P(y_i|Parents(y_i))$的值等于与结点$y_i$关联的条件概率表中的值。

可以用贝叶斯网在给定其他变量的观察值时推理出某些目标变量（如 ForestFire） 的值。 当然，由于所处理的是随机变量，所以一般不会赋予目标变量一个确切的值。真正需要推理的是目标变量的概率分布，它指定了在给与其他变量的观察值条件下，目标变量取每一可能
值的概率。在网络中所有其他变量都确切知道了以后，这一推理步骤是很简单的。在更通常 的情况下,我们希望在知道一部分变量的值（比如 Thunder 和 BusTourGroup 为仅有可用的观 察值）时获得某变量的概率分布（如 ForestFire）。一般地，贝叶斯网络可用于在知道某些变量的值或分布时计算网络中另一部分变量的概率分布。

而如果在网络结构的预先已知，并且变量可以从训练样例中完全获得时，通过学习得到条件概 率表就比较简单了。只需要象在朴素贝叶斯分类器中那样估计表中的条件概率项。但是如果网络结构已知，但只有一部分变量值能在数据中观察到，学习问题就困难得多了。

EM算法

在许多实际的学习问题框架中，相关实例特征中只有一部分可观察到。例如中医观察人身体有没有病，我们只能从患者的眼鼻等位置查看，这些特征可以获得，但是内部病变我们观察不到，这时候就需要我们从一部分特征去预测另一部分特征(例如从表象看出一个人患什么病)。
EM 算法(Dempster et al. 1977)，这 是存在隐含变量时广泛使用的一种学习方法。 EM 算法可用于变量的值从来没有被直接观察到的情形，只要这些变量所遵循的概率分布的一般形式已知。例如下面变量遵循的概率分布假定为正态分布。

接下来的算法介绍借鉴了http://blog.csdn.net/zouxy09/article/details/8537620 这篇博文的方法。

考虑数据D是一实例集合，它由k个不同正 态分布的混合所得分布所生成。例如同学们要检查身高，全体同学D是一个集合，它由两个不同正 态分布的混合所得分布所生成，即男生和女生。这里我们假设单个正态分布的选择基于统一的概率进行选择，并且 2个正态分布有相同的方差$σ^ 2$，且$σ^2$已知。
当男生和女生混在一起时，我们如何知道任一实例时男生还是女生呢，我们可以通过身高来判断男女，而假定男女的身高分布都满足正态分布，正态分布有相同的方差$σ^2$，且$σ^2$已知。
而我们的任务就是输出一个假设$h=<μ_1 …μ_k >$，它描 述了 k个分布中每一个分布的均值。我们希望对这些均值找到一个极大似然假设，即一个使$P(D|h)$最大化的假设h。这里也 <μ1…μk> <script type="math/tex" id="MathJax-Element-31"> <μ_1 …μ_k> </script>是k个正态分布的均值。就是说我们找一个满足极大似然假设的均值集合，使男生和女生各自的正态分布能最大化的分开，也就是说在第一个正态分布里抽到男生（的身高）概率最大，在第二个正态分布里抽到女生（的身高）概率最大。

EM的意思是“Expectation Maximization”，在我们上面这个问题里面，我们是先随便猜一下男生（身高）的正态分布的参数：如均值是多少。例如男生的均值是1米7（当然了，刚开始肯定没那么准），然后计算出每个人更可能属于第一个还是第二个正态分布中的（例如，这个人的身高是1米8，那很明显，他最大可能属于男生的那个分布），这个是属于Expectation一步。有了每个人的归属，或者说我们已经大概地按上面的方法将这200个人分为男生和女生两部分，我们就可以根据之前说的最大似然那样，通过这些被大概分为男生的n个人来重新估计第一个分布的参数，女生的那个分布同样方法重新估计。这个是Maximization。然后，当我们更新了这两个分布的时候，每一个属于这两个分布的概率又变了，那么我们就再需要调整E步……如此往复，直到参数基本不再发生变化为止。

这段话也就解释了EM算法的原理。接下来进行数学推导。

把每个实例的完整描述看作是三元组 <xi,zi1,zi2> <script type="math/tex" id="MathJax-Element-32"> </script>，其中 $x_i$是第i个实例的观测值， $z_{i1} , z_{i2}$表示两个正态分布中哪个被用于产生值 $x_i$。确切地讲， $z_{ij}$在 $x_i$由第j个正态分布产生时值为 1，否则为 0。这里 $x_i$是实例的描述中已观察到的变量， $z_{i1} , z_{i2}$是隐藏变量。在男女身高的例子中， $x_i$是第i个同学的身高， $z_{i1}$是1为男生， $z_{i2}$是1为女生。

如果$z_{i1}$和$z_{i2}$的值可知，就可以用式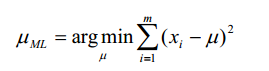（这个式子在贝叶斯（2）极大似然假设和误差平方最小化最后有推导）来解决均值$μ_1$和$μ_2$。因为它们未知，因此我们只能用EM算法。

我们令$Y=X∪ Z$代表全体数据。注意到未观察到的Z可被看作一随机变量，它的概率分布依赖于参数$μ$和已知数据X，也就是上面的正态分布。类似地， Y是一随机变量，因为它是由随机变量Z来定义的。我们将描述EM算法的一般形式。使用h来代表参数$μ$的假设值，而$h´$代表在EM算法的每次迭代中修改的假设。
EM 算法通过搜寻使 $E[lnP(Y|h´)]$最大的 $h´$来寻找极大似然假设$h´$。其中的$lnP(Y|h´)$最大也就是$P(Y|h´)$最大，$ln$会使乘运算变成加运算，使运算变得简单，而$P(Y|h´)$是给定假设 $h´$下全部数据 Y 的似然性。因为Y是 观察到的 X 和未观察到的 Z 的合并，我们必须在未观察到的 Z 的可能值上取平均，并以相应的概率为权值。这就是为什么需要计算期望值E的原因。
现定义一函数 $Q(h´|h)$，它在θ=h 和全部数据 Y的观察到的部分 X 的假定之下求 $E[lnP(Y|h´)]$。

$$Q(h´|h) = E[lnP(Y|h´)|h,X]$$
接着EM算法重复下面两步直至收敛。
步骤 1：估计（ E）步骤：使用当前假设 h 和观察到的数据 X来估计 Y上的概率分布以 计算 $Q(h´|h)$。
$$Q(h´|h) \leftarrow E[lnP(Y|h´)|h,X]$$
步骤 2：最大化（ M）步骤：将假设 h 替换为使 Q 函数最大化的假设 h´： $$h \leftarrow \max_{h'}Q(h'|h)$$

若此似然函数$P(Y|h´)$有单个的最大值时， EM 算法可以收敛到这个对 h´的全局的极大似然估计。否则，它只保证收敛到一个局部最大值。