4.1 极大似然估计
定义
所谓极大似然法( maximum likelihood method )是指选择使事件发生概率最大的可能情况的参数估计方法。
极大似然法包括2个步骤:
1)建立包括有该参数估计量的似然函数( likelihood function )
2)根据实验数据求出似然函数达极值时的参数估计量或估计值
对于离散型随机变量,似然函数是多个独立事件的概率函数的乘积,该乘积是概率函数值,它是关于总体参数的函数。
对于连续型随机变量,似然函数是每个独立随机观测值的概率密度函数的乘积,则似然函数为:
若yi 服从正态分布,则
,上式可变为:
求解的技巧:
为了计算上的方便,一般将似然函数取对数,称为对数似然函数,因为取对数后似然函数由乘积变为加式.
求极大似然估计量可以通过令对数似然函数对总体参数的偏导数等于0来获得.
例子:
设y1 , y2 , … , yn是正态总体的随机样本,求正态分布参数的极大似然估计量。
现假定在参数估计当中缺少数据Z,也就是我们在进行极大似然估计时有其他未知变量存在的情况下,我们如何解决在未知变量存在这种场景去进行参数估计呢?这就引入了EM算法
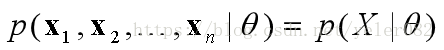
EM算法是一种迭代优化策略,由于它的计算方法中每一次迭代都分两步,其中一个为期望步(E步),另一个为极大步(M步),所以算法被称为EM算法(Expectation Maximization Algorithm)。其基本思想是:首先根据己经给出的观测数据,估计出模型参数的值;然后再依据上一步估计出的参数值估计缺失数据的值,再根据估计出的缺失数据加上之前己经观测到的数据重新再对参数值进行估计,然后反复迭代,直至最后收敛,迭代结束。
4.2 贝叶斯学习
4.2.1贝叶斯决策
- 目标:为了确定最可能的假设,给定数据D加上关于H中各种假设的先验概率的任何初始知识。
- h的先验概率P(h):它反映了我们所拥有的关于h是正确假设(在观察数据之前)任何背景知识的可能性。
- D的先验概率P(D):它反映了在不知道哪个假设h成立的情况下观察训练数据D的概率。
- 观测D条件概率,P(D | h):它表示观测数据D在假设h的条件下的概率。
- h的后验概率,P(h | D):它表示观测训练数据D给定h的概率。它反映了我们在看到训练数据D之后h持有的可信度,这是机器学习研究人员感兴趣的数据。
贝叶斯定理允许我们计算P(h | D):P(h|D)=P(D|h)P(h)/P(D)
目标:从给定观察数据D的一组候选假设H中找出最可能的假设h。
MAP(Maximum A Posteriori,最大后验概率) Hypothesis:
hMAP = argmax h∈H P(h|D)= argmax h∈H P(D|h)P(h)/P(D)= argmax h∈H P(D|h)P(h)
如果H中的每个假设都是先验的,那么我们只需要考虑数据D给定的可能性h,P(D | h)。然后,hMAP成为最大似然,hML= argmax h∈H P(D|h)P(h)
案例:
给定:m个类,训练样本和未知数据 目标:给每个输入数据标记一个类属性
两个阶段 1)建模/学习:基于训练样本学习分类规则. 2)分类/测试:对输入数据应用分类规则
什么是最优分类器?
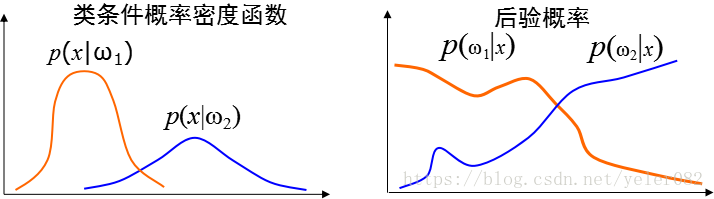
已有:类条件概率密度函数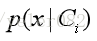
MAP决策:
以后验概率为判决函数:
选择一个类别使得K取最大值:
这产生了最佳性能,最小的错误概率:
实现这种最佳性能的分类器称为贝叶斯分类器。
决策的风险:
做决策要考虑决策可能引起的损失。
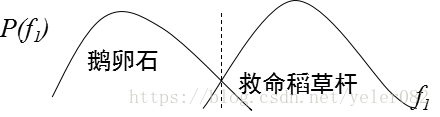
以医生根据白细胞浓度判断一个人是否患血液病为例:没病(ω1)被判为有病(ω2) ,还可以做进一步检查,损失不大;有病(ω2)被判为无病(ω1) ,损失严重。
Decision Risk table
The risk to make a decision: classify x (belong to class j) to class i, so:
Decision Rule:
基于Bayes决策的最优分类器的使用前提与问题转化
Bayes决策的三个前提:
①类别数确定 ②各类的先验概率P(Ci)已知 ③各类的条件概率密度函数p(x|Ci)已知
问题的转换:
⑴基于样本估计P(Ci)和p(x|Ci) ⑵基于样本直接确定判别函数
基于Bayes决策的最优分类器的其它trick
类的先验概率P(Ci)的估计方法:
①用训练数据中各类出现的频率估计 ②依靠经验
类条件概率密度p(x|Ci)估计的两种主要方法:①参数估计:概率密度函数的形式已知,而表征函数的参数未知,通过训练数据来估计
最大似然估计、最大后验估计
②非参数估计:密度函数的形式未知,也不作假设,利用训练数据直接对概率密度进行估计
Parzen窗法
4.2.2贝叶斯估计与预测
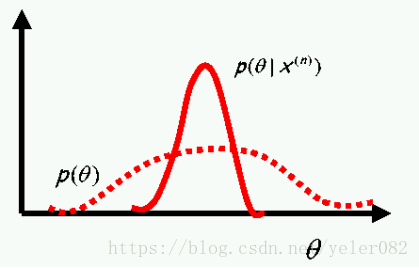
贝叶斯学习认为(要估计的参数向量)是一个随机变量。
在我们观察数据之前,这些参数由一个通常非常宽泛的先验描述。 一旦我们观察到数据,我们就可以利用贝叶斯公式来找到后验。由于参数的某些值比其他值更符合数据,因此后验比先前更窄。这是贝叶斯学习
4.3 朴素贝叶斯方法
- 朴素贝叶斯学习模型(NB )
假定特征向量的各分量间相对于决策变量是相对独立的,也就是说各分量独立地作用于决策变量。
降低了学习的复杂性
在许多领域,表现出相当的健壮性和高效性
- NB的特点
推理复杂性与网络节点个数呈线性关系









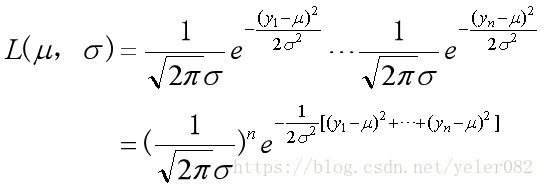
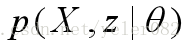

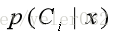
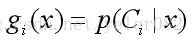
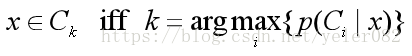
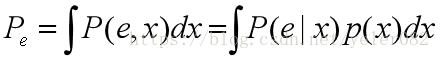

















 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








